сх.7-017

Задача № 5.

Задание:

Для заданной балки требуется:

1. Раскрыть статическую неопределимость при EJ = const.

2. Построить эпюры M_xи Q_y.

3. Сделать деформационную проверку.

4. Определить из расчета на прочность номер двутавра по ГОСТ.

Материал 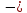Ст3.

5. Определить угол поворота сечения A.

P, кН	M, кН∙м	a, м	b, м	c, м	[σ], МПа
1	17	1	2,1	2,7	160

Решение :

1. Раскроем статическую неопределимость.

1). Определим степень статической неопределимости балки как разность между числом неизвестных опорных реакций и числом независимых уравнений равновесия: n = 4 – 3 = 1

Следовательно, балка один раз статически неопределима;

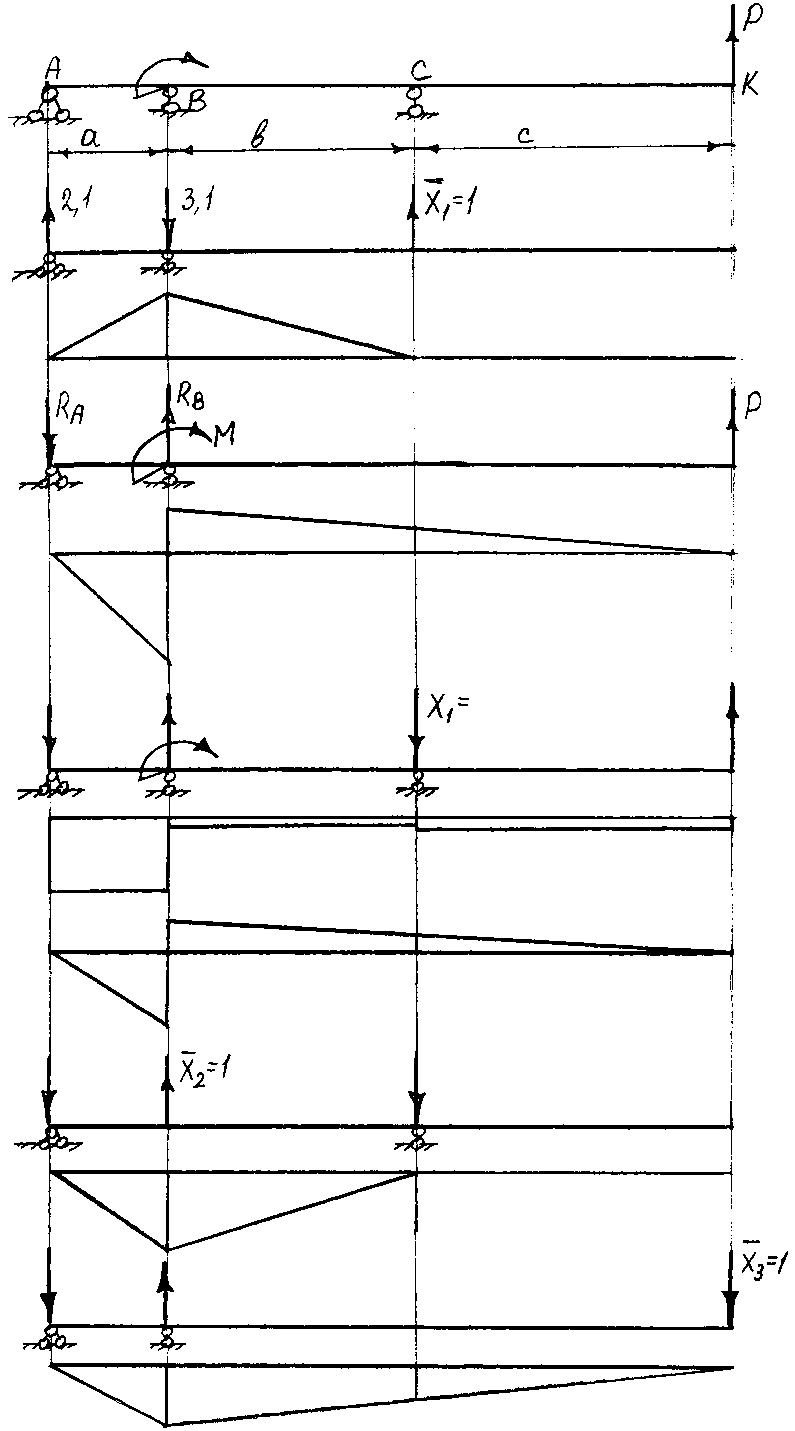
2).Выбираем основную систему;

3).Составим каноническое уравнение метода сил:

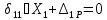
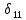- перемещение точки приложения единичной силы от действия этой же силы;

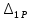- перемещение точки приложения единичной силы от действия внешних нагрузок;

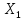- неизвестная сила.

Для определения 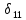нагрузим первую основную систему только силой Х₁=1

Заменим подвижную опору в т.С, реакцией Х₁

Строим единичную эпюру 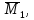для данной балки для этого вначале определяем реакции опор А и В.

 Ма = 0 ; Rв · а 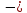Х₁ · (а + b) = 0;

Rв = 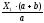= = 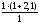3,1

 М_В = 0 ; R_А · a - Х₁ · b = 0;

R_А = 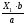= = 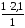2,1

Тогда

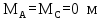
Применив формулу Мора ₁₁ =

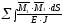
Определим ₁₁ перемножением эпюру 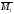«саму на себя»

₁₁ = 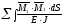= 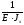· ( · 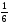2 · 2,1 · 2,1 + 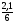· 2 · 2,1 · 2,1) =

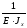= · (1,47 + 3,087) =

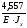
Прогиб _1q определим перемножив с помощью правила Верещагина эпюры .

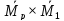Для построения эпюры 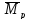нагружаем первую основную систему только внешними силами , убрав одну опору. Для полученной схемы определим реакции опор, а затем построим эпюры ;

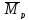 Ма = 0 ; 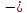Rв · а + М 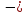Р · (а + b + с) = 0;

Rв = 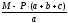= = 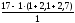11,2 кН.

 М_В = 0 ; 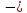R_А · a + М 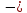Р · (b + c) = 0;

R_А = 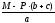= = 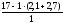12,2 кН.

Проверочное уравнение .  F_У = 0 ; Rв - R_А + Р = 0

11,2 - 12,2 + 1 = 0. Условие статики 0  0 выполняется, следовательно, реакции опор определены верно.

Построим эпюру М_р

Определим значения моментов в характерных точках.

М_А = 0 кН м ; М_В1 = R_А · а = 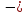12,2 · 1 = 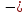12,2 кН м

М_К = 0 кН м ;

М_В2 = Р · (b + c) = 1 · (2,1 + 2,7) = 4,8 кН м.

М_С = Р · c = 1 · 2,7 = 2,7 кН м.

По полученным данным строим эпюры изгибающих моментов.

Вычислим значение прогиба _1q

_1q = =

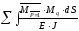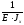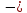
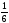=· [ · 2 · 12,2 · 2,1 + 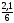· (2 · 4,8 ·2,1 + 2,7 · 2,1) ] =

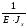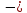= · (8,54 + 9,0405) =

2. Раскроем статическую неопределимость.

Решаем уравнение деформации ( 1 )

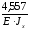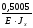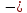
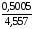
 Х₁ + = 0 ; Отсюда Х₁ = 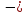0,11 кН ;

Для вновь полученной схемы определим реакции опор.

 М_А = 0 ; 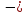Rв · а + М + X₁ · (а + b)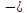Р · (а + b + с) = 0;

Rв=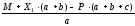==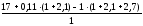 11,54 кН.

 М_В = 0 ; 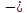R_А · a + М + X₁ · b 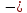Р · (b + с) = 0;

R_А = 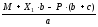= = 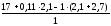12,43 кН.

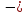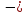Проверочное уравнение .  F_У = 0 ; Rв R_АX₁ + Р = 0

11,54 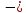12,43 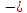0,11 + 1 = 0. 12,54 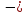12,54 = 0.

Условие статики 0  0 выполняется, следовательно, реакции опор определены верно.

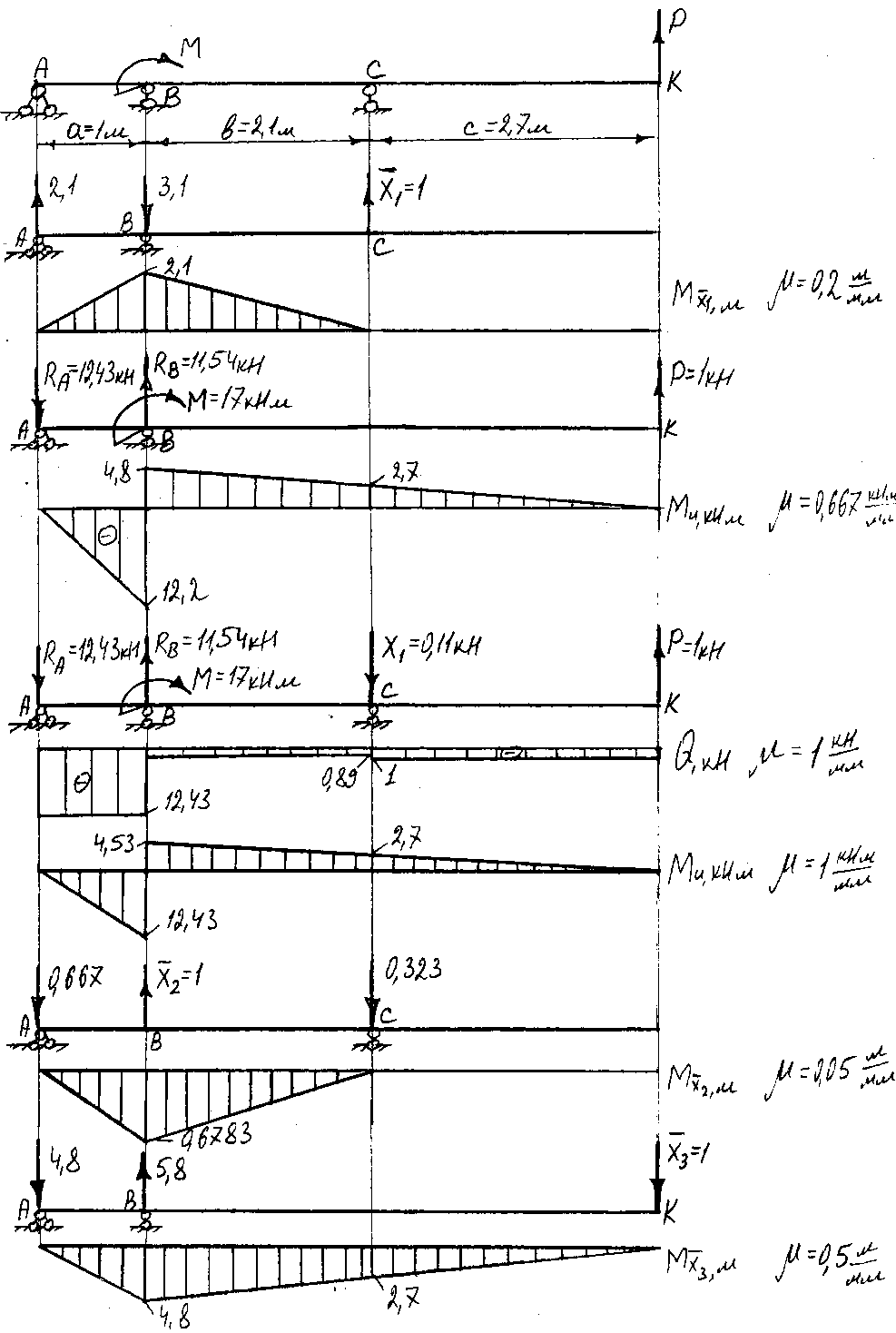
3. Построим эпюры Q и Ми

Балка имеет три участка : АВ , ВС и СК

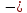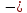Участок АВ Q_А = Q_В = R_А = 12,43 кН

Участок ВС Q_В = Q_С = 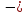R_А + R_В = 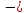12,43 + 11,54 = 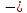0,89 кН

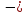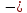Участок СК Q_С = Q_Д = Р = 1 кН

Определим значения моментов в характерных точках.

М_А = 0 кН м ; М_К = 0 ;

М_В1 = 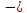R_А · а = 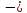12,43 · 1 = 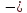12,43 кН м;

М_С = Р · с = 1 · 2,7 = 2,7 кН м;

М_В2 = 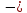Х · b + Р · (с + b) =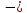0,11 · 2,1 + 1 · 4,8 = 4,57 кН м;

По полученным данным строим эпюры поперечных сил и изгибающих моментов.

5. Деформационная проверка.

Определяем перемещение _2Р в основной системе, т.е. прогиб балки в месте, где установлена опора В. Он должен быть равен нулю.

Для этого приложим единичную силу в опоре В и определим перемещение в т. В (перемножим единичную эпюру с грузовой)

Определяем реакции опор А и С от единичной силы.

 Ма = 0 ; Rc · (а + b) 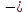Х₂ · а = 0;

Rс = 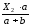= = 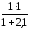0,323

 М_с = 0 ; 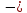R_А · (а + b) + Х₂ · b = 0;

R_А = 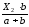= = 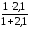0,677

Тогда

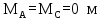
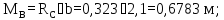
_2q ==

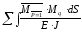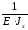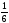= · [· 2 · 12,43 · 0,6783 +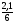· (- 2 · 4,57 · 0,6783 - 2,7 · 0,6783)] =

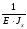= · (2,8104 - 2,8108)  0

6.Вычисляем размеры сечения данной балки из условий прочности на изгиб. Условие прочности :  =  [ ]

Wx  Ми.max./ [] = ( 12,43 · 10)⁶/160 = 77,7 см ³

Из таблицы стандартных профилей примем двутавр № 14

Где А_ст = 17,4 см ² ; W_х = 81,7 см ³ ; J_х = 572 см ⁴ ;

7. Определим прогиб в сечении K.

Для этого в т.К приложим единичную силу и построим эпюру от единичной силы. Перемножим единичную эпюру с грузовой по правилу трапеции.

Определим реакции опор от единичной силы.

 Ма = 0 ; 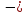Rв · а + Х₃ · (а + b + с) = 0;

Rв = 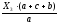= = 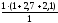5,8

 М_В = 0 ; 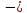R_А · a + Х₃ · (b + с) = 0;

R_А = 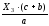= = 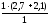4,8

Тогда

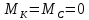
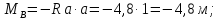
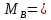
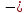Х₁ · с = 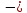1 · 2,7 = - 2,7 м.

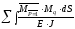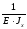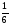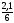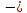_К = =· [· 2 · 4,8 · 12,43 +· (2 · 4,8 · 4,57 –

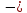2 · 2,7 · 2,7 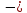2,7 · 4,8 – 4,57 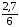· 2,7) +· 2 · 2,7 · 2,7 ] =

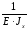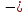
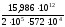= · (19,888 – 29,313 – 6,561) = = - 14 мм.

Сечение поднимается вверх, противоположно направлению единичной силы.

8