Рабочая профессия / Отчёт лаб 3

Лабораторная работа 3

СИСТЕМЫ СЧИСЛЕНИЯ: ПЕРЕВОД ЧИСЕЛ

Цель работы: организация средствами Excel автоматического выполнения операций над представлениями чисел в позиционных системах счисления.

Содержание работы

1. Реализация перевода чисел в десятичную систему счисления.

2. Реализация перевода чисел из десятичной системы счисления.

3. Сложение чисел в позиционных системах счисления.

4. Проведение экспериментов и решение задач.

Выполнение работы

В соответствии с пояснениями к выполнению работы создаем листы В десятичную, Из десятичной и Сложение в книге Excel:

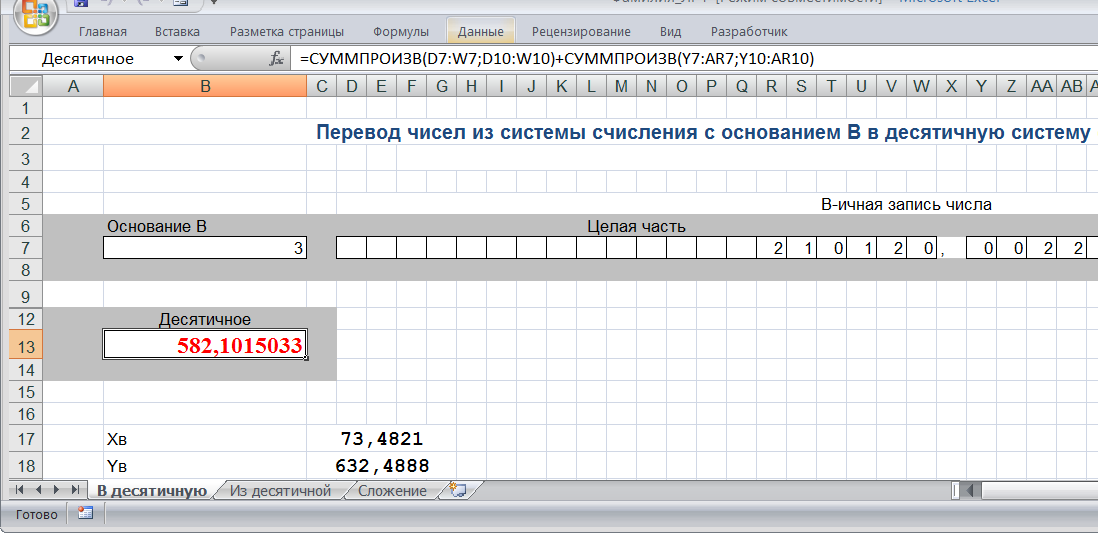
Вопросы

4.1.

1). Как представляется число 1190,625₁₀ в двадцатеричной системе счисления? 2). Сколько значащих двадцатеричных цифр оно содержит?

1) 1190,625₁₀ = 2 19 10. 12 10₂₀,

2) 5 значащих цифр.

4.2.

1). Почему дробь получается периодической?

Дробь получается периодической, потому, что при умножении очередной дробной части от предыдущего шага на основание системы счисления получаем число, которое уже было прежде. Естественно процесс зацикливается.

2). В каких случаях дробь с конечным числом цифр точно переводится в дробь с конечным числом цифр?

Дробь с конечным числом цифр точно переводится в дробь с конечным числом цифр, если в процессе умножения получается целое число. Далее сколько ни умножай 0 на что-то, получится 0.

4.3. Вопросы:  Сколько неточных последних разрядов содержат результаты выполняемого «машиной» перевода десятичной дроби 0,1₁₀ в системы счисления с основаниями 1) B = 9; 2) B = 11; 3) B = 12?

Ответы:

1) 5; 2) 6; 3) 8

4.4.

Вопросы: 1). Можно ли было без осуществления перевода предсказать появление в конце числа двух нулей? 2). Сколько нулей будет в конце его троичной записи?

Ответы:

1) Да, так как число 999999999 естественно делится нацело на 9. А результат этого деления число 111111111, девять единиц, по признаку делимости числа на 9 (сумма цифр делится на 9) так же делится на 9.;

2) 333333333 111111111 – уже можно гарантировать 3 нуля в конце (так же признак деления числа на 3 – деление суммы цифр числа на 3).

4.5. В [1] утверждается, что шестнадцатеричное число делится на 15, если сумма его цифр делится на 15. Переведите в шестнадцатеричную запись целое число N = 2595. 1). Чему равна сумма его цифр? 2). Подтверждается ли признак?

Ответы:

1. 2595,1 = А23,1999999999999А₁₆.

2. 10+2+3+1+9*12+10= 134. Не делится на 15

4.6. Проверьте следующий признак делимости на 7 числа, записанного в восьмеричной системе счисления: число делится на 7 тогда и только тогда, когда на 7 делится сумма его цифр. Переведите 651 в восьмеричную систему. 1). Какой получился результат перевода? 2). Выполняется ли упомянутый признак делимости на 7?

Ответы: 1) 651 = 1213₈. Сумма цифр 7.

2) 1213₈. / 7=135₈. Признак делимости выполняется

4.7. Перейдите на лист «В десятичную». Введите 2 в ячейку B8. Задайте для перевода из двоичной системы число 0,1. В результате автоматического перевода в десятичную дробь получилась дробь 0,5 с конечным числом значащих цифр. Задайте для перевода любую другую двоичную дробь и посмотрите на результат. 1). Объясните, почему всегда получается дробь с конечным числом значащих цифр?

Ответ: Потому что фактически дробное число по основанию 2 это

Σxi/2^-i, где i= 1, 2, ….; xi ={0, 1}. То есть слагаемые это степени деления 1 на 2. А это всегда конечная дробь.

4.8. Перейдите на лист «Сложение». Удалите все цифры из диапазона слагаемых. Не бойтесь нечаянно удалить содержимое ячеек суммы (в которых находятся формулы) - ведь лист Вы защитили. Выполните несколько сложений в двоичной системе счисления. Вопросы: 1). При каких условиях наш «сумматор» будет работать неправильно из-за переполнения его разрядной сетки? 2). Какой вид имеет наибольшее значение правильно вычисляемой суммы в двоичной записи? 3). Какое это будет десятичное число?

Ответы: 1) При условии, если произошло переполнение старшего разряда.

2) и 3) Наибольшая правильная сумма 1111111111.1111111111111111₂ = 1023.999985

4.9. С помощью всех трех листов выполните следующие действия:

- переведите число 2460,73₈ в десятичную систему счисления;

- переведите полученное десятичное число с помощью листа «Из десятичной» обратно в восьмеричную систему. 1). Получилось ли вновь исходное число?

2460,73₈ -> 1328, 921875

1328, 921875 -> 2460,73₈ тот же результат.

4.10.

Работа с числами в соответствии с вариантом 6.

Основание системы	Число XB	Число YB	Суммирование в сумматоре
9	073,4821	632,4888	705,9709
10	66.546105776558	515.55540313977	573.0877914952
3	2110.11220200222	201002.11222222000	203112,224424222

X_B  X_C  X_B  X₁₀ , X₁₀  X_C

073,4821  66.546105776558  2110,112202010

Y_B  Y_C  Y_B  Y₁₀ Y₁₀  Y_C

632,4888  515,5554031  201002,11222221

X_B + Y_B = Z_B

073,4821 + 632,4888 = 705,9709

Z_B  Z₁₀ ;

705.9709₉ = 573.0877914952₁₀

X_C + Y_C = Z_C

2110,112202010 + 201002,11222221 =203112,224424222

Z_C  Z'₁₀

5