на флешку студентам / МЕТОДИЧКИ / Методички (мех) / № 4

Работа 4

ПРОВЕРКА ТЕОРЕМЫ ГЮЙГЕНСА-ШТЕЙНЕРА

Принадлежности: прибор, секундомер, масштабная линейка.

Введение . Вращательное движение твердого тела около неподвижной оси описывается уравнением

M=J*ε (1)

где М - момент силы относительно оси вращения, ε - угловое ускорение, J - момент инерции тела относительно оси вращения.

С огласно теореме Гюйгенса-Штейнера момент инерции тела относительно любой оси равен моменту инерции этого тела относительно параллельной оси, проходящей через центр инерции тела, сложенному с произведением массы тела на квадрат расстояния между осями. Так, момент инерции диска D (рис.1) относительно оси 0, перпендикулярной к плоскости чертежа, равен J=J₀+ml² , где J0 - момент инерции диска относительно оси О'.

Следует заметить, что момент инерции тела определяется по указанной теореме лишь в том случае, когда тело совершает вращательное движение около оси О. Если тело движется поступательно по окружности радиуса (рис.1), то его можно рассматривать как материальную точку, масса которой сосредоточена в центре инерции тела. В этом случае момент инерции тела относительно оси О будет равен

.

В данной работе экспериментально проверяется справедливость теоремы Гюйгенса-Штейнера.

Описание прибора. Прибор состоит из вала -AA со шкивом (рис.2). Вал может вращаться в шарикоподшипниках, укрепленных в настенном кронштейне. На шкив намотан тонкий стальной трос, к свободному концу которого прикреплена сдвоенная гиря Р . Она служит для приведения вала и связанных с ним частей прибора в равномерно ускоренное вращение. На середине вала, перпендикулярно ему, укреплен стержень CC. На концах его имеются два массивных металлических диска Д, плоскости которых перпендикулярны валу АА. Металлические диски могут либо вращаться, либо двигаться поступательно по окружности с радиусом l относительно оси AA. Вид движения задается установкой стопора ВВ в определенное положение.

Измерения. Намотав трос на шкив K , опускают без толчка груз и измеряют время его падения t с высоты h . Ускорение груза Р будет равно a=2 h/t² , а угловое ускорение системы ε=a/r, где r - радиус шкива. Эти ускорения будут зависеть от момента инерции всей системы и величины груза Р. При постоянном Р ускорения зависят только от момента инерции системы. Если диски застопорены, момент инерции системы будет равен

В противном случае

(моментом инерции вала АА, шкива K и стержня CC пренебрегаем по сравнению с моментом инерции дисков).

При постоянном грузе Р приближенно можно считать, что моменты сил, обуславливающие ускоренное вращение системы, одинаковы. На этом обосновании запишем

или

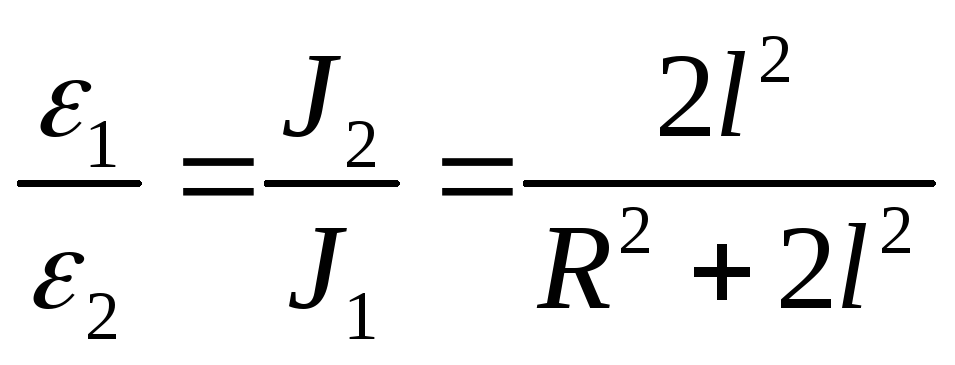
с другой стороны

таким образом, окончательно имеем

Этот вывод экспериментально проверяется в данной задаче. Время падения груза Р измеряют дважды (при закрепленных дисках - t₁ , и свободных дисках - t₂ ). Число измерений для каждого случая должно быть не менее 10. Выполнив опыт с грузом Р, развинчивают гирю и повторяют измерения в том же порядке с грузом Р₁. Масштабной линейкой измеряют величины l и R . Результаты измерений заносят в таблицы.

l= R=

№	t1	T12	t2	t22

По этому же образцу строят таблицу для уменьшенного груза Р₁.

Находят отношение

и сравнивают его с

Оценивают погрешности А и В.

Контрольные вопросы.

1. Дайте определение поступательного и вращательного движения тела.

2. В каком случае в данной работе диски участвуют в поступательном, а в каком - во вращательном движении?

3. Сформулируйте теорему Гюйгенса-Штейнера.

4. Чему равна сила натяжения нити в момент опускания груза?

5. Нарисуйте схематически экспериментальную установку.

Литература

Стрелков С. П. Механика. - М.: Наука 1975, гл. 7, § 59

Савельев И. В. Курс общей физики. Т. 1. - М.: Наука, 1977, гл.5, § 39,39