на флешку студентам / МЕТОДИЧКИ / Методички (мех) / № 9

Кафедра общей физики ПГУ

Механическая лаборатория

Лабораторная работа № 9

Лабораторная работа №9

ИЗУЧЕНИЕ СИЛ ТРЕНИЯ И ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ.

Принадлежности: установка ЛТЭ (наклонная плоскость, исследуемый брусок с деревянной и металлической поверхностью).

Цель работы:

1. Определить коэффициент трения скольжения между бруском с деревянной и металлической поверхностями и деревянной поверхностью;

2. Определить максимальное значение коэффициента трения покоя.

Введение. Если твердое тело скользит по поверхности, то между телом и поверхностью возникают силы трения скольжения. Сила трения скольжения F_тс, действующая на тело, направлена противоположно относительной скорости этого тела. На поверхность, по которой скользит тело, также действует сила трения скольжения, направленная противоположно силе трения скольжения, действующей на тело (в соответствии с третьим законом Ньютона). Если соприкасающиеся поверхности достаточно гладкие, то сила трения скольжения F_тс пропорциональна силе нормального давления N и практически не зависит от скорости скольжения тела. В этом случае выполняется закон

F_тс=k∙N (1)

Безразмерный множитель k называется коэффициентом трения.

Если твердое тело лежит на поверхности, то оно может оставаться в покое и в том случае, когда на тело действуют достаточно малые тангенциальные силы, т. е. силы, действующие вдоль поверхности. В этом случае между телом и поверхностью возникает сила трения покоя, которая компенсирует приложенную силу.

При возрастании внешней силы увеличивается и сила трения покоя. Однако сила трения покоя не может расти беспредельно. Существует максимальная сила трения покоя, которая для достаточно гладких поверхностей пропорциональна силе нормального давления. Максимальная сила трения покоя F_max несколько меньше F_тс, но для достаточно гладких поверхностей это различие может быть несущественным. Если внешняя сила превысит F_max, то тело начнет скользить по поверхности.

Рассмотрим движение груза массой m по наклонной плоскости.

Уравнение движения груза по наклонной плоскости имеет вид

, (2)

где α – угол наклона плоскости.

Определим значение k и скорость движения груза υ.

Предполагая, что зависимость k (υ) в пределах условий эксперимента будет незначительной, можно считать, что ускорение движения не изменится. Тогда для случаев, когда начальная скорость υ₀=0.

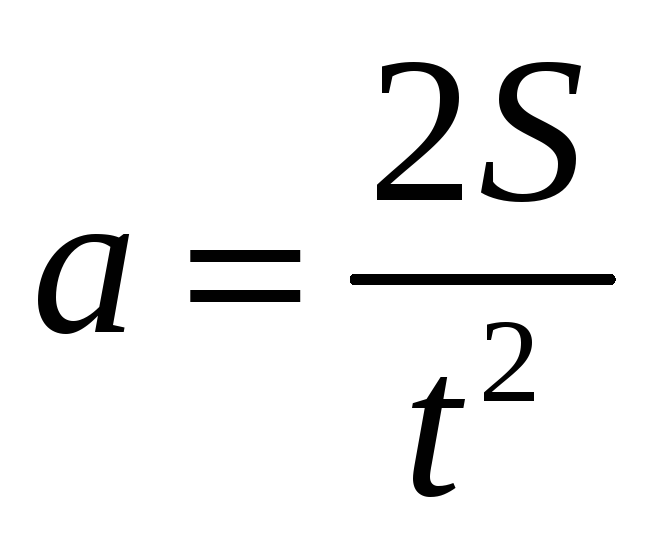(3)

Используя формулы (1), (2) и (3), получим

. (4)

Описание установки.

1

5

1

Для проведения лабораторной работы используется установка ЛТЭ рис.2. Установка состоит из механического блока БМ2-02 и электронного секундомера СЭ1. Механический блок состоит из наклонной плоскости 1. Стопорный винт 6 позволяет изменять угол

наклона плоскости и устанавливать заданный угол с помощью отчетного устройства 4 и указателя 5. Электромагнит 7 служит для фиксации исследуемого бруска. Кнопка «стоп» с ограничителем 2 используется для остановки образца. Для определения времени движения исследуемого образца по наклонной плоскости используется электронный секундомер 8. Включение секундомера производится кнопкой «Сеть». При этом загорается индикатор времени и индикатор первого режима (в данной лабораторной работе используется только первый режим, не следует бездумно нажимать другие кнопки, это может привести к порче прибора!). Для включения отчета времени используется кнопка «Пуск». После нажатия «Пуск» включается электромагнит, начинается отсчет времени. После срабатывания фотодатчика отсчет времени прекращается, выключается электромагнит. Остановку счета времени можно произвести нажатием кнопки «Стоп/Сброс». Повторное нажатие этой кнопки приведет к сбросу показаний индикатора.

Измерения. 1. Установить плоскость 1 (рис.3) под углом α=20°. Для этого нужно ослабить стопорный винт 6 и повернуть плоскость на требуемый угол по часовой стрелке. Контроль угла осуществляется при помощи указателя 5 и отсчетного устройства 4. Зафиксировать положение стопорным винтом 6. Значение угла записать в таблицу.

2. Секундомер СЭ1 перевести в режим 1. Переключить тумблер 6 (рис.2) “от себя”.

3. На верхний правый конец наклонной плоскости установить брусок металлической поверхностью вниз, где он будет зафиксирован магнитным полем.

4. Включить кнопку «Пуск» секундомера. Записать значение времени движения образца в таблицу №1. Опыт провести не менее 5 раз. Отсчет пройденного расстояния S провести по линейке 3.

5. Перевернуть брусок деревянной поверхностью вниз. Повторить пункты 2,3,4. Данные записать в таблицу №2.

6. Повторить пункты 1,2,3,4 для углов α=30° или α=40° (в соответствии с указанием преподавателя).

Упражнение №2

Определить значение коэффициента трения покоя и его максимальное значение. Увеличивая угол наклона плоскости найти минимальный угол при котором брусок начинает скользить. Тангенс этого угла равен максимальному коэффициенту трения покоя

k_тр.п. = tgα.

Обработка результатов измерений.

1. По формуле (4) определить коэффициент трения скольжения k для бруска с деревянной и металлической поверхностью.

2. Найти среднее арифметическое коэффициента k.

3. Определить полуширину доверительного интервала по формуле Стьюдента

4.Окончательный результат записать в виде k= с указанием доверительной вероятности p=0,95.

Таблица№1

S= (м)

№	материал	T	α	k		2
1.	Дерево-алюминий		α=20°
2.
3.
4.
5.
Сред.
1.	Дерево-алюминий		α=30° (40°)
2.
3.
4.
5.
Сред.

Для бруска с другой поверхностью строится аналогичная таблица.

Контрольные вопросы

1. Какие виды трения Вам известны?

2. Перечислите все факторы от которых зависит сила трения скольжения.

3. Зависит ли сила трения скольжения от ускорения?

4. Какие законы, определяющие силу трения, Вам известны.

5. Выведите формулу (4).

6. Зависит ли от угла наклона плоскости α коэффициент трения скольжения?

7. Какие выводы можно сделать на основании проведенного эксперимента?

Список рекомендуемой литературы

1. Савельев И. В. Курс общей физики. В 3-х т. М.: Наука, 1977. Т I. Гл. II, § 13, 15; Гл. V, § 41.

2. Детлаф А. А., Яворский Б. М., Милковская Л. Б. Курс физики. В 3-х т. М.: Высшая школа

- 4 -