7

Лабораторная работа №32

ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ ВЕЛОСИПЕДНОГО КОЛЕСА

Цель работы:

Определить момент инерции велосипедного колеса различными способами.

Принадлежности: установка, секундомер, штангенциркуль и миллиметровая линейка.

Введение. Уравнение вращательного движения твердого тела имеет вид

, (1)

где – момент инерции тела, - его угловое ускорение, - момент приложенных к телу сил.

Момент инерции – аналог массы. Как масса – мера инертности при поступательном движении, так и момент инерции – мера инертности при вращательном движении. При вращении тела вокруг различных осей моменты инерции различны. Величина момента инерции относительно какой-либо оси определяется пространственным распределением элементарных масс тела – геометрией масс. Аналитической вычисление величины момента инерции производится путем интегрирования выражения

, (2)

где - плотность вещества в элементарном объеме , находящегося на расстоянии от оси вращения.

При сложной форме поверхности, ограничивающей тело, и неравномерном распределение плотности аналитический подсчет величины момента инерции может быть достаточно сложной задачей. Экспериментально же определение момента инерции осуществимо легко.

В настоящей задаче измеряется момент инерции колеса двумя различными способами.

Упражнение №1. Определение момента инерции методом колебаний.

О

Рис. 1

писание установки и теория. Велосипедное колесо 1 может вращаться с малым трением вокруг горизонтальной оси 2 (рис. 1). На внутренней стороне обода колеса симметрично по диаметру укреплены два очень легких и одинаковых по весу металлических стаканчика 3. К колесу на нити прикреплен груз 4. Помещая груз в один из стаканчиков, получаем физический маятник, который может колебаться вокруг положения равновесия, отклоняясь влево и вправо от вертикали, проходящей через центр колеса.

Пренебрегая моментом сил трения, можем записать уравнение движения колеса вместе с грузом

, (3)

где - момент инерции колеса со стаканчиками, - момент инерции груза относительно оси колеса, - масса груза, - расстояние между центром груза и осью колеса, - ускорение силы тяжести, - угол отклонения колеса от положения равновесия, - угловое ускорение колеса.

Если (малые углы отклонения), то можно написать

, (4)

Уравнение (4) является уравнением гармонических колебаний. Решением его будет функция вида:

t, (5)

где - амплитуда колебаний, - циклическая частота, - период колебаний колеса.

Из уравнения (5), дифференцируя его по времени, получаем

. (6)

Сопоставляя уравнения (4) и (6), находим

. (7)

Учитывая, что диаметр грузика во много раз меньше диаметра колеса, можем считать грузик материальной точкой и положить

. (8)

Тогда из уравнений (7) и (8) получаем

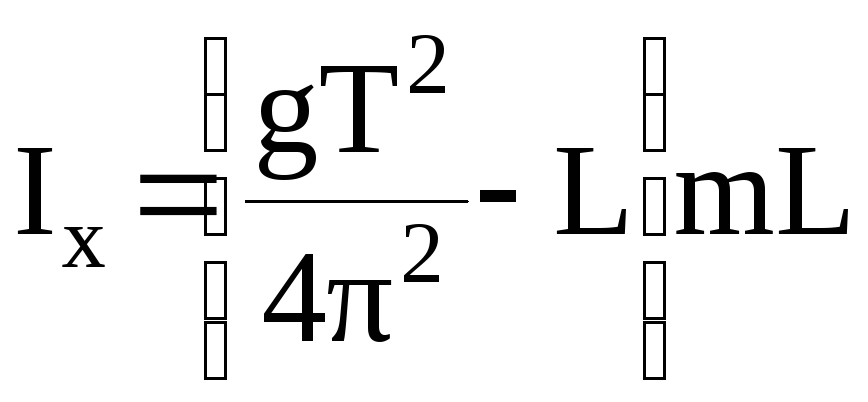. (9)