Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский государственный национальный исследовательский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

№108

.doc

Скачиваний:

Добавлен:

13.03.2016

Размер:

4.92 Mб

Скачать

☆

Кафедра общей физики ПГУ

Механическая лаборатория

Лабораторная работа № 108

Лабораторная работа №108

ИЗУЧЕНИЕ ДВИЖЕНИЯ МАЯТНИКА МАКСВЕЛЛА

Принадлежности: установка ФМ-12, сменные кольца.

Цель:

1.Изучение движения маятника Максвелла.

2.Определение момента инерции маятника.

Введение.

Движение маятника Максвелла – один из примеров колебательных процессов в механике. Так же как и другие маятники, маятник Максвелла характеризуется повторением всех фаз своего движения через некоторый интервал времени ( период колебаний ) и переходом потенциальной энергии в кинетическую и обратно. Однако, в отличие от математического, физического или пружинного маятников, маятник Максвелла совершает принципиально негармонические колебания. Характерные графики изменения координаты, скорости и ускорения маятника представлены на рис.1.

Рис 1.

Маятник Максвелла представляет собой диск, насаженный на ось и подвешенный с помощью бифилярного подвеса к опоре (рис.2). В верхнем положения маятника нити намотаны на ось, в нижнем (положении равновесия) — полностью размотаны.

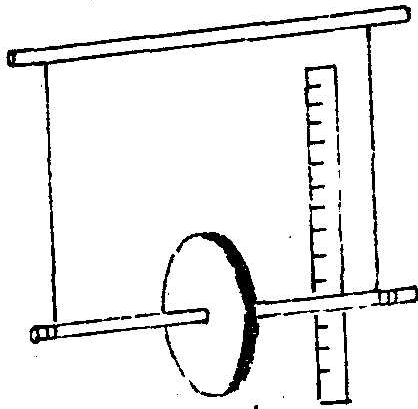
Рис. 2

Цикл движения маятника Максвелла может быть разбит на три стадии, а именно спуск, удар, поднятие вверх. В соответствии с этим силы, действующие на маятник, должны быть подразделены на силы длительного действия (при спуске и поднятии) и силы кратковременного действия (удар). В первом случае эти силы не изменяются во времени, во втором они резко нарастают и убывают. При перемещении маятник участвует в прямолинейном вертикальном и вращательном движениях.

Графики на рисунке 1 относятся к прямолинейному движению центра инерции. Опускание маятника из верхнего в нижнее положение и подъем обратно представляют собой одно полное колебание, имеющее период Т . Движение из верхнего положения в нижнее (или наоборот) составляет половину колебания и длится Т/2 сек. Поскольку движение маятника является периодическим, то вполне достаточно исследовать движение в течение одного периода. Более того, опускание и подъем маятника происходят по одинаковым сценариям, а это означает, что характер движения можно изучить на примере только опускания (или только подъема) маятника.

Кинетическая энергия маятника равна

где угловая скорость маятника, J - момент инерции

маятника. Поскольку >>1, кинетическая энергия , связанная с поступательным движением, мала по сравнению с энергией вращательного

движения . Это является главным отличительным признаком маятника

Максвелла. Характерной особенностью маятника Максвелла является малая потеря энергии при ударе , т.е. близкий к единице коэффициент

восстановления скорости . Именно благодаря этому в данной системе можно наблюдать колебания, т.е. многократное повторение цикла движения вниз - вверх, а сама система называется “маятником”.

Описание установки

Маятник Максвелла представлен на рис.3. и включает в свой состав: штатив 1, кронштейн 2с фотодатчиком 3 и с электромагнитами 4, диск 5 с осью, подвешенной на двух нитях 6, узел 7 подвески и регулировки исходного положения маятника, комплект из трех сменных колец с различными моментами инерции, блок электронный 8.

Блок электронный включает в свой состав корпус 8,на передней панели которого находится электронное табло .Управление блоком осуществляется кнопками СТАРТ и СТОП. При нажатии кнопки «СТАРТ» на блоке электромагниты 4 должны обесточится, маятник должен раскручиваться, таймер должен произвести отсчет времени, а в момент пересечения маятником оптической оси фотодатчика отсчет времени должен прекратиться.

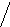
Рис.3.

Теория движения маятника Максвелла.

Для количественного исследования движения маятника Максвелла используем уравнения динамики твердого вращающегося тела. Эти уравнения представляют собой второй закон Ньютона для поступательного и вращательного движения

(1)

(2)

где M и J масса и момент инерции, и - линейное и угловое ускорения, и — силы и моменты сил, действующих на маятник.

Поскольку вектора ускорения и сил направлены вдоль вертикальной прямой, то можно выбрать систему координат, в которой из всех проекций уравнения (1) останется только одна ненулевая проекция на ось z (рис.4). То же самое можно сказать об уравнении (2), т.к. вращение происходит вокруг оси, не меняющей своей ориентации в пространстве. Тогда система уравнений будет выглядеть так:

Рассмотрим силы и моменты сил, действующих на маятник (рис.4). Определим момент сил относительно оси симметрии маятника. Тогда уравнения движения будут выглядеть следующим образом:

Рис. 4

(3)

(4)

где r - радиус оси маятника, - сила натяжения нити, - ускорение свободного падения. Кроме того, как нетрудно заметить, характеристики вращательного и поступательного движения связаны между собой:

(5)

Из уравнений (3), (4) и (5) можно определить любую из величии, если известны остальные. Например, можно рассчитать ускорение свободного падения, если знать параметры маятника М, J, r и измерить ускорение его движения a (остальные переменные в уравнениях исключаются). Можно рассчитать вес Р маятника в движении, который будет равняться силе натяжения нитей подвеса . Применим систему (3), (4) и (5) для вычисления момента инерции маятника Максвелла. Преобразования системы дадут следующую формулу для момента инерции

(6)

Для определения ускорения а, воспользуемся известной формулой кинематики

(7)

где h - путь, проходимый телом за время t.

Измеряя время, за которое маятник проходит некоторый путь, зная массу маятника и радиус его оси, можно рассчитать момент инерции маятника.

Этот же момент инерции можно рассчитать, если знать массы и геометрические размеры составных частей маятника (при известной оси вращения). Считая, что маятник вращается вокруг своей оси симметрии, момент инерции определим по формулам:

(8)

где - момент инерции оси маятника,

- момент инерции диска маятника

- момент инерции сменного кольца маятника, надеваемого на диск.

Отдельные моменты инерции вычислим следующим образом

(9) (10) (11) где , , - соответственно массы оси, диска, кольца, , , - внешние радиусы оси, диска, кольца.

R_о= 0,004м, R_д= 0,021м, R_к = 0,048м; m₀= 0,019кг, m_д = 0,1кг.

Сравнение момента инерции, определенного экспериментально с помощью формулы (6), и момента инерции, рассчитанного теоретически по формуле (8), должно дать одинаковые результаты (с учетом погрешности измерении).

Измерения.

Внимание! Для предотвращения перегревания катушек электромагнитов – время непрерывной работы электромагнитов – не более 15 секунд, перерыв -5 секунд

. Установить нижний кронштейн с фотодатчиком 3 в крайнее нижнее положение шкалы так, чтобы плоскость кронштейна, окрашенная в синий цвет, совпадала с одной из рисок шкалы.
Надеть сменное кольцо на диск 5.
Установить с помощьустройства 7необходимую длину бифилярного подвеса таким образом, чтобы край среза сменного кольца маятника находился на 4-5 мм ниже оптической оси фотодатчика 3, при этом ось маятника должна занимать горизонтальное положение.
Нажать кнопку «СЕТЬ» измерительного блока 8.Приэтом включаются электромагниты и табло индикации.
Вращая маятник по часовой стрелке, зафиксировать его в верхнем положении при помощи левого (ближе к стойке) электромагнита, при этом необходимо следить за тем, чтобы нить наматывалась на ось виток к витку.
Нажать кнопку «СТАРТ» на блоке. После остановки секундомера определить время движения маятника. Показания секундомера t записать в таблицу 1
Повторить измерения для выбранного кольца 5-8 раз.
Надеть на диск другое сменное кольцо. Провести еще две серии экспериментов.
Определить по миллиметровой шкале при помощи визира путь h маятника.

Обработка результатов измерений.

Рассчитать ускорение движения маятника а по формуле (7).Найти среднее значение для ускорения.
Вычислить момент инерции J по формуле (6). Усреднить J для каждого кольца.
Обработать результаты каждой серии измерений по Стьюденту.
Рассчитать моменты инерции для всех трех вариантов маятника по формуле (8) и сравнить с результатами расчета по формуле (6). Все данные маятника приведены на установке.

Таблица 1

R_о= 0,004м, R_д= 0,021м, R_к = 0,048м; m₀= 0,019кг, m_д = 0,1кг.