на флешку студентам / МЕТОДИЧКИ / Методички (мех) / № 100

Работа № 100

Колебания в системе с двумя степенями свободы

(связанные маятники)

Цель работы

В системе с двумя степенями свободы (два связанных пружиной физических маятника) экспериментально проверить предполагаемую зависимость между частотой биений и частотами нормальных колебаний при различной величине связи.

Теоретический расчет колебательного процесса в экспериментальной установке.

Экспериментальная установка (рис. 1) состоит из одинаковых физических маятников, соединенных спиральной пружиной (П), измерительной шкалы (Ш) и секундомера. Маятники представляют собой стержни (С) с укрепленными на них чечевицами (Ч). Пружину можно перемещать вдоль стержней С. Этим обеспечивается изменение связи между маятниками.

[рис. 1]

Экспериментальная установка представляет собой систему с двумя степенями свободы. Это значит, что для определения системы в пространстве (т.е. положения каждого из мятников) необходимо задать две координаты. Такими координатами могут быть либо – величины горизонтальных смещений маятника, либо (рис. 2) – величины угловых смещений и т.д., существенно лишь то, что требуется задание двух чисел.

Очевидно, в рассматриваемой экспериментальной установке будут происходить колебательные процессы. Но будут ли эти процессы гармоническими, т.е. будут ли изменяться углы отклонений и по закону синуса или косинуса с течением времени? В общем случае, наверное, нет. Действительно, отклоним только один маятник в сторону и посмотрим, что произойдет с другим маятником. Из-за воздействия пружины другого маятник придет, очевидно, в движение, будет происходить его постепенное раскачивание. Однако такое движение не является гармоническим, поскольку амплитуда этих колебаний изменяется с течением времени (это движение невозможно представить в виде синусоиды – см. ниже рис. 5).

[рис. 2]

С другой стороны, если мы оба маятника отклоним в одну и ту же сторону на одинаковые углы, то связывающая маятники пружина практически «не будет работать», так как она не сжимается и не растягивается. При этом, если трение и сопротивление воздуха мало, то оба маятника будут совершать гармонические колебания (рис. 3). Нетрудно понять, что если отклонить оба маятника в разные стороны на одинаковые по величине углы (рис. 4), то оба маятника также будут совершать гармонические колебания.

[рис. 3]

Таким образом, в системе связанных маятников будут происходить как гармонические, так и негармонические колебания. Гармонические колебания в системе с несколькими степенями свободы называются нормальными колебаниями системы.

Нормальные колебания представляют особый интерес, поскольку любые негармонические колебаниями являются суперпозициями (или линейными комбинациями) этих нормальных колебаний.

[рис. 4]

Переходим теперь к количественному описанию колебаний маятников. Исходные уравнения – основные уравнения динамики вращательного движения.

Пусть каждый из маятников имеет момент инерции J и массу m. Центр инерции расположен на расстоянии от оси вращения, пружина жесткости k прикреплена к маятникам на расстоянии r от оси вращения (см. рис. 2).

На каждый из маятников действует два момента сил: момент силы тяжести и момент силы связи. Будем считать колебания малыми, т.е. полагаем малыми углы отклонения маятников

(1)

так что

(2)

Согласно рис. 2 величина сжатия пружины равна

(3)

Учтя при вычислении моментов сил приближенные равенства (2), основные уравнения динамики вращательного движения можно записать в виде

(4)

(5)

Введем обозначения:

(6)

Тогда уравнения (4) и (5) после деления на величину J перепишутся в следующей форме:

(7)

(8)

Если убрать пружину (т.е. положить формально жесткость равной нулю) или поднять пружину вверх (), то третьи члены в уравнениях обратятся в нуль, и движение каждого из двух маятников опишется уравнением гармонических колебаний

(9)

причем -собственная частота колебаний одного отдельно взятого физического маятника.

Именно различие уравнений (7), (8) и (9) показывает, что в общем случае движение в системе с двумя степенями свободы происходит не по гармоническому закону. Пусть и - начальные угловые отклонения маятников. Можно проверить путем подстановки, тогда уравнения (7), (8) имеют решения

(10)

(11)

Здесь введены обозначения

(12)

или (13)

Соотношения (10), (11) демонстрируют тот факт, что в общем случае колебания маятников не являются гармоническими, а представляют собой суперпозицию (комбинацию) двух гармонических колебаний – с частотами и (очевидно, последние два колебания и есть нормальные).

Теперь уместно задать вопрос: при каких условия возбуждения в нашей экспериментальной установке возникают все же чисто гармонические (т.е. нормальные) колебания? Точный количественный ответ, дают, конечно, соотношения (10) и (11), из которых видно, что бывают такие ситуации:

а) нормальные колебания первого типа. Пусть в начальный момент t = 0 оба маятника были отклонены в одну и ту же сторону на равные углы (см. рис. 3):

. (14)

Тогда (см выражения (10) и (11)):

(15)

(16)

Оба маятника совершают синхронные гармонические колебания с частотой . Эта частота не зависит от наличия пружины (пружина «не работает»);

б) нормальные колебания второго типа. Пусть в начальный момент t = 0маятники были отклонены в разные стороны, но на равные углы (см. рис. 4)

. (17)

Тогда (см выражения (10) и (11)):

(18)

(19)

Оба маятника совершают в противофазе гармонические колебания с частотой . Частота больше частоты и растет с увеличением расстояния r от оси до места закрепления пружины (см. формулу (13)).

Таким образом, в рассматриваемой колебательной системе с двумя степенями свободы возможны два нормальных колебания, и их можно возбудить, если отклонить маятники в начальный момент времени согласно рис. 3 и 4.

Биения

Всякое отклонение начальных условий от (14) и (17) (т.е. ) возбуждает оба нормальных колебания. Так что движение каждого маятника будет представлять собой результат наложения (суперпозиции) нормальных колебаний обоих типов.

Действительно, положим, например, в соотношениях (10), (11)

(20)

Это значит, что в начальный момент t = 0 правый (второй) маятник отклонили вправо на угол , а левый маятник оставили в положении равновесия. При этом выражения (10), (11) переписываются так:

(21)

(22)

В нашей установке частоты и достаточно близки друг к другу. Удобно записать отмеченную суперпозицию в следующем виде (используя тригонометрические соотношения ):

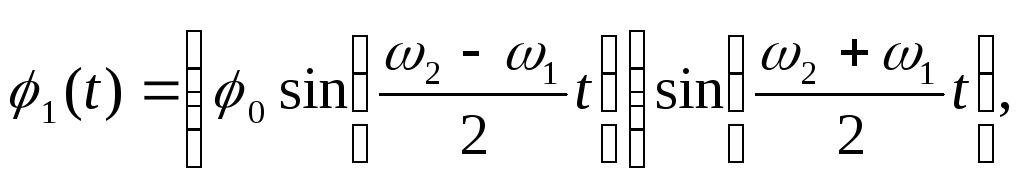(23)

(24)

В такой записи вторые сомножители описывают колебания с частотой

, (25)

а первые сомножители – колебания с частотой

. (26)

Поэтому , и первые сомножители меняются сравнительно медленно. Величины

(27)

(28)

можно назвать медленно изменяющимися амплитудами колебаний, описываемых вторыми сомножителями в соотношениях (23) и (24).

С какой же частотой изменяются сами амплитуды A₁ и A₂? Очевидно, с частотой .В самом деле, всякая частота (в данном случае в выражениях (27) и (28)) характеризует частоту появления «горбов» (или «впадин») вдоль синусоиды или косинусоиды. Когда мы находим модуль или , то «горбы» будут встречаться вдвое чаще. Это и означает, что A₁(t) и A₂(t) периодически меняются с удвоенной частотой:

(29)

Таким образом, соотношения (23) и (24) говорят о том, что оба маятника испытывают биения: маятники совершают колебательное движение (с частотой ) с периодически нарастающими и убывающими амплитудами (с частотой ). Это движение есть результат суперпозиции двух нормальных колебаний с близкими частотами и представляет собой негармоническое колебание. Биения возникают при всяком одновременном возбуждении обоих типов нормальных колебаний.

На рис. 5 показан характер движения маятников. Пунктирными линиями даны A₁(t) и A₂(t), называемые теперь амплитудами биений. Частоты периодических изменений этих амплитуд биений обоих маятников одинаковы и равны:

. (30)

[рис. 5]

Частота называется частотой биений. Период биений и период колебаний Т равны соответственно:

Тот факт, что частота биений равна разности нормальных частот (30), можно пояснить еще следующим образом. Амплитуды биений (27) и (28) – модули функций и изменяются периодически через период биений (см. рис. 5), который можно найти из условия

откуда так как то получаем .

Таким образом, теоретическое рассмотрение процессов, происходящих в экспериментальной установке, предсказывает следующее:

1. Первоначальное отклонение маятников в одну и ту же сторону на равные углы возбуждает нормальные колебания первого типа. Причем, частота совпадает с частотой колебаний одного отдельно взятого маятника и не зависит от положения пружины;

2. первоначальное отклонение маятников в разные стороны, но на равные по величине углы, возбуждает нормальные колебания второго типа. Частота больше частоты . С увеличением расстояния r от оси вращения до места закрепления пружины частоты возрастает;

3. ;

4. при первоначальном отклонении маятников на неравные углы (в частности, в ситуации рис. 5) каждый из маятников совершает сложное негармоническое движение, являющееся суперпозицией (суммой) нормальных колебаний обоих типов. При этом наблюдается явление биений с частотой биений . С ростом величины r частота возрастает за счет увеличения величины .

В настоящей работе проводится экспериментальная проверка этих теоретических выводов.

Измерение частот

Все частоты определяются по измерениям времени (t_N) N колебаний. Если Т – период колебаний, то

Таким образом, по измеренному времени t можно рассчитать частоты

(31)

Задание к лабораторной работе

1. Определить частоту собственных колебаний маятников (Снять пружину). По времени 30 колебаний определить собственную частоту колебаний каждого маятника в отдельности. Если частоты маятников отличаются друг от друга больше, чем на 1%, то их необходимо уравнять, перемещая чечевицу одного из маятников по стержню (штанге).

2. Установить пружину (положение пружины задается преподавателем). Измерить и по времени 10 колебаний, возбуждая нормальные колебания в соответствии с рис.3 и 4. Измерить при этом же положении пружины частоту биений по 5 биениям, возбуждая их по схеме рис. 5. Производя измерения наблюдайте за движением одного маятника, начинайте измерения, когда амплитуда его равна нулю.

3. Выполнить пункт 2 еще для четырех положений пружины, поднимая пружину вверх.

4. В отчете необходимо письменно сделать выводы относительно справедливости теоретических предсказаний:

   1. о равенстве = и независимости от расстояния r;

   2. об изменении сростом расстояния r;

   3. о равенстве

   4. об изменении частоты биений с увеличением расстояния r.

Чтобы выводы сделать более очевидными, представьте свои результаты в виде соответствующих графиков. (Какие графики необходимо представить?).

Контрольные вопросы

1. Какова цель настоящей работы?

2. Справедливость каких теоретических выводов проверяется в работе?

3. Какие графические зависимости Вы ожидаете получить?

4. Какие формулы являются рабочими?

5. Как получить расчетную формулу для оценки погрешностей измерений величины ?

6. Каким образом Вы будете измерять частоты нормальных колебаний и частоту биений?

7. Что такое число степеней свободы?

8. Напишите основное уравнение динамики вращательного движения.

9. Как вывести уравнения (4) и (5)?

10. Почему уравнение (7) или (8) не описывает чисто гармонические колебания?

11. Какие колебания называются нормальными?

12. Что такое явление биений? Когда возникают биения?

13. Почему биения не представляют собой гармонические колебания?

14. Что такое амплитуда биений? Изобразите график зависимости амплитуды биений от времени.

15. Почему частота биений равна разности нормальных частот, а не их полуразности?

16. Подтверждают ли ваши экспериментальные результаты теоретические выводы?

8