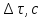на флешку студентам / МЕТОДИЧКИ / Методички (мол) / Формат / 217

Кафедра общей физики ПГУ

Лаборатория молекулярной физики

Лабораторная работа № 217

Лабораторная работа № 217

ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ ТВЕРДЫХ ТЕЛ

Принадлежности: установка ФПТ1-8.

Цель работы:

1. Измерение теплоемкости твердых тел при высоких температурах.

2. Проверка выполнимости закона Дюлонга и Пти для исследуемых образцов.

Введение. Теплоемкостью С тела называется отношение элементарного количества теплоты δQ, сообщенного телу в каком-либо процессе, к соответствующему изменению температуры тела

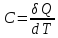
Теплоемкость зависит от массы тела, его химического состава, термодинамического состояния и вида процесса сообщения теплоты.

Удельной теплоемкостью С_уд называется теплоемкость единицы массы однородного вещества. Для однородного тела

,

где m – масса вещества.

Молярной теплоемкостью называется теплоемкость одного киломоля (моля) вещества

,

где µ- молекулярный вес вещества.

Согласно классической теории теплоемкости при не слишком низких температурах, молярная теплоёмкость химически простых веществ в кристаллическом состоянии одинакова и равна 25 Дж/(моль∙к). Это утверждение составляет содержание закона Дюлонга и Пти, установленного опытным путем.

Между частицами, образующими кристаллическую решетку твердых тел, существуют силы взаимодействия. Расположение частиц в узлах кристаллической решетки отвечает минимуму их взаимной потенциальной энергии. При смещении частиц из положения равновесия в любом направлении появляется сила, стремящаяся вернуть частицу в первоначальное положение, вследствие чего возникают ее колебания.

При точном рассмотрении задачи необходимо учитывать, что частицы в решетке взаимодействуют друг с другом и их, колебания надо рассматривать как связанные. Однако при достаточно высоких температурах, когда энергия становится большой, колебания частиц можно рассматривать приближенно как н друг от друга.

Полная энергия частицы U равна сумме кинетической Е_к и потенциальной Е_п:

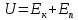
Колебания частиц в решетке приближенно являются гармоническими. При этом как кинетическая, так и потенциальная энергии гармонических колебаний частицы являются периодическими функциями времени и их средние значения и равны друг другу: = Поэтому среднее значение полной энергии

(1)

С другой стороны, из кинетической теории идеального газа известно, что средняя кинетическая энергия одноатомных молекул (изолированных частиц)

(2)

где k – постоянная Больцмана, Т - абсолютная температура.

Поскольку, как было отмечено, атомы или ионы кристаллической решетки при достаточно высоких температурах колеблются независимо друг от друга, к ним также применима формула (2). Тогда из (1) и (2) имеем,

. (3)

Полную внутреннюю энергию одного моля твердого тела получим, умножив среднюю энергию одной частицы на число независимо колеблющихся частиц, содержащихся в одном моле, т. Е. на постоянную Авогадро N_А:

(4)

где R - молярная газовая постоянная.

Для твердых тел, вследствие малого коэффициента теплового расширения при постоянном давлении и постоянном объеме практически не различаются. Поэтому общее выражение теплоемкости твердого тела совпадает со значением молярной теплоемкости при : . Из формулы (4) окончательно следует, что

. (5)

Подставляя численное значение молярной газовой постоянной, получаем =25Дж/(моль∙К)

Это равенство выполняется, с довольно хорошим приближением для многих веществ при комнатной температуре, для более низких температур наблюдается отклонение от него рис.1. Вблизи абсолютного нуля молярная теплоемкость всех тел пропорциональна Т^З, и только при достаточно высокой, характерной для каждого вещества температуре начинает выполняться равенство (5).

Строгая теория теплоемкости твердых тел создана Эйнштейном и Дебаем. Она учитывает, что колебания частиц в кристаллической решетке не являются независимыми и что энергия колебательного движения квантована.

Описание установки. Установка ФПТ1-8 рис . 2 представляет собой конструкцию настольного типа, состоящую из трех основных частей:

1) блока приборного БП-8,

2) блока рабочего элемента РЭ-8,

3) стойки.

На лицевой панели блока приборного БП-8 (1) находятся цифровой контроллер для измерения времени, вольтметр, амперметр, органы управления и регулирования установки. Визуально блок разделен натри функциональных узла: узел «ИЗМЕРЕНИЕ».узел «НАГРЕВ», узел «СЕТЬ».

Узел «ИЗМЕРЕНИЕ» состоит из цифрового контроллера для измерения времени, амперметра, вольтметра, и осуществляет замер величины тока, напряжения, времени проведения опыта.

Узел «НАГРЕВ» осуществляет включение и регулирование нагрева нагревателя.

Узел «СЕТЬ» осуществляет подключение установки к сети питающего напряжения.

Блок РЭ-8 (2) представляет собой коробчатый конструктив, укрепленный на горизонтальном основании стойки (3) . Несущими узлами блока РЭ-8 являются панель и кронштейн, скрепленные между собой винтами. Спереди блок РЭ -8 закрыт съемным экраном из орг стекла. При выполнении работы экран навешивается на заднюю стенку блока РЭ-8.

На панели расположен цифровой контроллер (6) для измерения температуры, внизу на выступающей панели размещены образцы (5) из различных материалов и рукоятка для установки образцов в нагреватель.

Нагреватель (4) состоит из металлического кожуха, теплоизолирующего материала, калориметра, с намотанной на нем спиралью, ручки для выталкивания образца из калориметра. В калориметр вмонтирован датчик контроллера для измерения температуры.

Принцип действия установки.

Удельная теплоемкость определяется по формуле

где Q- количество теплоты, поглощенное образцом при нагревании на ∆Т, m- масса образца, ∆Т – разность конечной и начальной температур.

Если для нагревания пустого калориметра на ∆Т требуется Q₁ джоулей тепла , а для нагрева калориметра с исследуемым образцом на ∆Т требуется Q₂ джоулей тепла, то на нагрев самого образца идет

В установке ФТПТ1-8 нагрев производится пропусканием тока через нагреватель.

Количество теплоты, выделяемое нагревателем

где I- ток через нагреватель, U- напряжение на нагревателе, τ- время нагрева.

Если мощность нагрева остается постоянной в течении всего эксперимента, то

где τ₁- время нагрева пустого калориметра на ∆Т, τ₂- время нагрева калориметра с образцом на ∆Т.

Тогда удельная теплоемкость определяется по формуле

, (6)

где I- сила тока, U- напряжение, m-масса исследуемого образца,∆τ=τ₂-τ₁.

Методика проведения эксперимента заключается в следующем. Сначала определяется зависимость приращения температуры от временя для пустого калориметра 1, затем для калориметра с исследуемым телом 2. При этом ток I_н в обмотку нагревательной спирали калориметра неизменен. В отсутствие теплообмена с окружающей средой эти зависимости были бы линейными. В реальных условиях графики этих зависимостей имеют вид, изображенный на рис. 3.

Для нагревателя пустого калориметра на ∆t градусов потребуется отрезок времени τ₁, а для нагревания калориметра с телом потребуется больший промежуток времени τ₂. Удельная теплоемкость исследуемого образца определяют по формуле (6).

Рис. 3

Измерения.

Внимание! Эксперимент проходит достаточно быстро, необходимо внимательно изучить порядок работы, заранее подготовить таблицу и научиться пользоваться секундомером.

1. Включить тумблер «вкл.» в модуле питания «сеть», расположенный на лицевой панели приборного блока (1) БП-8 рис.1.

2. Снять съемный экран из оргстекла с блока РЭ-8(2). При выполнении работы экран навешивается на заднюю стенку РЭ-8.Убедиться, что в калориметре (4) отсутствует образец. Плотно закрыть крышку калориметра. Записать над таблицей начальную температуру.

3. Подготовить к работе секундомер. Включить тумблер «вкл» в модуле «нагрев» приборного блока (1). При этом загорается сигнальная лампа. Регулятором модуля установить заданную мощность нагрева (сила тока I = 0.5А, напряжение U устанавливается автоматически). Записать в таблицу значения I и U. Во время измерений следить, чтобы показания вольтметра и амперметра не изменялись.

4. В таблицу №1 записывать показания температуры на цифровом контроллере(6) через каждые 30 секунд (не менее 10-12 измерений). Не нагревать пустой калориметр выше 70⁰. После окончания измерений выключить нагреватель, открыть крышку калориметра. В течение 30 минут охладить калориметр. Для быстрого охлаждения использовать вентилятор. Вентилятор включается через блок питания. Пока охлаждается калориметр построить график зависимости разности температур ∆Т от времени нагревания τ (см. обработку результатов).

5. Определить массу одного из испытуемых образцов (5).Записать материал из которого изготовлен образец. Поместить образец в калориметр. Плотно закрыть крышку калориметра. Повторить п.3 и 4 Внимание! Максимальная температура нагрева 70 ⁰ С. Данные записать в таблицу №2

6. После окончания измерений выключить нагреватель, открыть крышку калориметра и с помощью специального приспособления извлечь образец из калориметра. Будьте осторожны! Образец горячий!

Обработка результатов измерений.

1. Вычислить разность температур, где - температура пустого калориметра через каждые 30 c после начала нагрева,- температура пустого калориметра до начала нагрева. Результаты записать в таблицу№1.

2. Построить графики зависимости от времени τ для пустого калориметра.

3. Вычислить разность температур, где 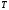- температура калориметра с исследуемым образцом через каждые 30 c после начала нагрева,- температура калориметра с исследуемым образцом до начала нагрева. Результаты записать в таблицу№2.

4. На том же графике построить график зависимости от времени τ для калориметра с исследуемым образцом.

5. Найти по графику для трех значений разности температурразность времени ∆τ нагревания калориметра с исследуемым образцом и пустого калориметра (см. рис 3).Данные записать в таблицу №3.

6. Рассчитать по формуле (6) удельную теплоемкость для значений разности времени нагревания, определенных в п. 5. Определить среднее значение удельной теплоемкости.

7. Рассчитать молярную теплоемкость по формуле: , где µ – молярная масса материала (для одноатомных веществ атомная и молярная массы совпадают), - удельная теплоемкость тела.

8. Результаты измерений сравнить с табличными значениями и с предсказаниями закона Дюлонга и Пти.

9. Проанализировать построенные графики. Написать заключение о проведенной работе.

Таблица№1

Т₀= I = U=

№	материал
1	пустой	30
2		30

Таблица№2

m=

№	материал	τ,с
1		30
2		30

Таблица№3

№	материал
1
2
3
Ср.

Табличные данные.

Материал	Молярная масса, µ	Удельная теплоемкость C,
Медь	63.5∙10-3	7.29 ∙102
Алюминий	27 ∙10-3	8.9 ∙ 102
Сталь	56 ∙ 10-3	4.6 ∙102

Контрольные вопросы.

1. Что называется удельной, молярной теплоемкостью вещества?

2. Чем отличается теплоемкость газов и твердых тел?

3. Как получить закон Дюлонга и Пти исходя из классической теории теплоемкости?

4. Сравните (при помощи табличных значений) молярную теплоемкость жидких, твердых и газообразных тел. Сделайте выводы. Сравните удельные теплоемкости этих тел. Сделайте выводы. Как зависит теплоемкость от агрегатного состояния вещества?

5. Объясните принцип действия установки и методику выполнения лабораторной работы.

6. В чем проявляется недостаточность классической теории теплоемкостей?

Теплоемкость газообразного водорода при Т=290 К, С_v=4,90. Запишите значение теплоемкости в системе СИ.

8