
Диф.ур-м с запазд.аргументом
.pdf
ВВЕДЕНИЕ
Министерство образования Российской Федерации
Международный образовательный консорциум «Открытое образование»
Московский государственный университет экономики, статистики и информатики
АНО «Евразийский открытый институт»
Э.А.Геворкян
Дифференциальные уравнения с запаздывающим аргументом
Учебное пособие Руководство по изучению дисциплины
Сборник задач по дисциплине Учебная программа по дисциплине
Москва 2004
Геворкян Э.А. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ: Учебное пособие, руководство по изучению дисциплины, сборник задач по дисциплине, учебная программа по дисциплине / Московский государственный университет экономики, статистики и информатики – М.: 2004. – 79 с.
Геворкян Э.А., 2004
Московский государственный университет экономики, статистики и информатики, 2004
2
Содержание |
|
Учебное пособие |
|
Введение................................................................................................................................. |
6 |
ГЛАВА I. Метод шагов решения дифференциальных уравнений |
|
с запаздывающим аргументом.................................................................................................. |
7 |
1.1 Классификация дифференциальных уравнений с |
|
отклоняющимся аргументом. Постановка начальной задачи................................................ |
7 |
1.2 Дифференциальные уравнения с запаздывающим аргументом. Метод шагов. ........ |
9 |
1.3 Дифференциальные уравнения с разделяющимися |
|
переменными и с запаздывающим аргументом....................................................................... |
12 |
1.4 Линейные дифференциальные уравнения с запаздывающим аргументом................ |
13 |
1.5 Дифференциальные уравнения Бернулли с запаздывающим аргументом. ............... |
14 |
1.6 Дифференциальные уравнения в полных дифференциалах |
|
с запаздывающим аргументом.................................................................................................. |
15 |
ГЛАВА II. Периодические решения линейных дифференциальных уравнений |
|
с запаздывающим аргументом.................................................................................................. |
18 |
2.1. Периодические решения линейных однородных дифференциальных уравнений |
|
с постоянными коэффициентами и с запаздывающим аргументом...................................... |
18 |
2.2. Периодические решения линейных неоднородных дифференциальных |
|
уравнений с постоянными коэффициентами и с запаздывающим аргументом................... |
20 |
2.3. Комплексная форма ряда Фурье.................................................................................... |
23 |
2.4. Отыскание частного периодического решения линейных неоднородных |
|
дифференциальных уравнений с постоянными коэффициентами и запаздывающим |
|
аргументом разложением правой части уравнения в ряд Фурье........................................... |
25 |
ГЛАВА III. Приближенные методы решения дифференциальных уравнений |
|
с запаздывающим аргументом.................................................................................................. |
27 |
3.1. Приближенный метод разложения неизвестной функции |
|
с запаздывающим аргументом по степеням запаздывания.................................................... |
27 |
3.2. Приближенный метод Пуанкаре. .................................................................................. |
28 |
ГЛАВА IV. Дифференциальные уравнения с запаздывающим аргументом, |
|
появляющемся при решении некоторых экономических задач |
|
с учетом временного лага ............................................................................................................... |
30 |
4.1.Экономический цикл Колецкого. Дифференциальное уравнение
сзапаздывающим аргументом, описывающего изменение
запаса наличного капитала........................................................................................................ |
30 |
4.2. Характеристическое уравнение. Случай вещественных |
|
корней характеристического уравнения................................................................................... |
33 |
4.3. Случай комплексных корней характеристического уравнения................................. |
35 |
4.4. Дифференциальное уравнение с запаздывающим аргументом, |
|
описывающего динамику национального дохода в моделях с лагами |
|
(потребление пропорционально национальному доходу)...................................................... |
37 |
4.5. Дифференциальное уравнение с запаздывающим аргументом, |
|
описывающего динамику национального дохода в моделях с лагами |
|
(потребление экспоненциально растет с темпом прироста)................................................... |
39 |
Литература.............................................................................................................................. |
41 |
3 |
|
Руководство по изучению дисциплины |
|
1. Сведения об авторах.......................................................................................................... |
44 |
2. Перечень основных тем..................................................................................................... |
45 |
2.1. Тема 1. Основные понятия и определения. Классификация |
|
дифференциальных уравнений с отклоняющимся аргументом. |
|
Дифференциальные уравнения с запаздывающим аргументом. ........................................... |
45 |
2.2. Тема 2. Постановка начальной задачи. Метод шагов решения |
|
дифференциальных уравнений с запаздывающим аргументом. Примеры........................... |
46 |
2.3. Тема 3. Дифференциальные уравнения с разделяющимися |
|
переменными и с запаздывающим аргументов. Примеры. .................................................... |
47 |
2.4. Тема 4. Линейные дифференциальные уравнения |
|
с запаздывающим аргументом. Примеры. ............................................................................... |
49 |
2.5. Тема 5. Дифференциальные уравнения Бернулли |
|
с запаздывающим аргументом. Примеры. ............................................................................... |
50 |
2.6. Тема 6. Дифференциальные уравнения в полных дифференциалах |
|
с запаздывающим аргументом. Необходимые и достаточные условия. Примеры.............. |
51 |
2.7. Тема 7. Периодические решения линейных однородных дифференциальных |
|
уравнений с постоянными коэффициентами и с запаздывающим аргументом. |
|
Примеры. ..................................................................................................................................... |
52 |
2.8. Тема 8. Периодические решения линейных неоднородных дифференциальных |
|
уравнений с постоянными коэффициентами и с запаздывающим аргументом. |
|
Примеры. ..................................................................................................................................... |
54 |
2.9. Тема 9. Комплексная форма ряда Фурье. Отыскание частного периодического |
|
решения линейных неоднородных уравнений с постоянными коэффициентами и с |
|
запаздывающим аргументом разложением правой части уравнения в ряд Фурье. |
|
Примеры. ..................................................................................................................................... |
55 |
2.10. Тема 10. Приближенное решение дифференциальных уравнений с |
|
запаздывающим аргументом методом разложения функции от запаздывания |
|
по степеням запаздывания. Примеры....................................................................................... |
56 |
2.11. Тема 11. Приближенный метод Пуанкаре нахождения периодического |
|
решения квазилинейных дифференциальных уравнений с малым параметром и |
|
с запаздывающим аргументом. Примеры. ............................................................................... |
57 |
2.12.Тема 12. Экономический цикл Колецкого. Дифференциальное уравнение
сзапаздывающим аргументом для функции К(t), показывающей запас наличного
основного капитала в момент t.................................................................................................. |
58 |
2.13. Тема 13. Анализ характеристического уравнения, отвечающего |
|
дифференциальному уравнению для функции K(t). ............................................................... |
59 |
2.14. Тема 14. Случай комплексных решений характеристического уравнения |
|
( ρ =α ±ιω ).................................................................................................................................. |
60 |
2.15. Тема 15. Дифференциальное уравнение для функции у(t), показывающего |
|
национальный доход в моделях с лагами капитальных вложений при условии, что |
|
функция потребления имеет вид c(t -τ ) = (1 - α ) у (t -τ ), где α - постоянная норма |
|
производственного накопления ................................................................................................ |
62 |
2.16. Тема 16. Дифференциальное уравнение для функции y(t), показывающего |
|
национальный доход в моделях с лагами капитальных вложений при условии, что |
|
функция потребителя имеет вид c(t −τ)= c(o)er (t −τ ) ............................................................... |
63 |
Сборник задач по дисциплине........................................................................................... |
65 |
Учебная программа по дисциплине................................................................................. |
77 |
4 |
|
Учебное пособие

ВВЕДЕНИЕ
Введение
Настоящее учебное пособие посвящено изложению методов интегрирования дифференциальных уравнений с запаздывающим аргументом, встречающихся в некоторых технических и экономических задачах.
Вышеуказанными уравнениями обычно описываются любые процессы с последействием (процессы с запаздыванием, с временной задержкой). Например, когда в исследуемом процессе значение интересующей нас величины в момент времени t зависит от величины x в момент времени t-τ, где τ – временной лаг (y(t)=f[x(t-τ)]). Или, когда значение величины y в момент времени t зависит от значения этой же величины в момент вре-
мени t-τ (y(t)=f[y(t-τ)]).
Процессы, описывающиеся дифференциальными уравнениями с запаздывающим аргументом встречаются и в естественных, и в экономических науках. В последних это связано как с существованием временного лага в большинстве связях цикла общественного производства, так и с наличием инвестиционных лагов (период от начала проектирования объектов до ввода в действие на полную мощность), демографических лагов (период от рождения до вступления в трудоспособный возраст и начала трудовой деятельности после получения образования).
Учет временного лага при решении технических и экономических задач имеет важное значение, так как наличие лага может существенно повлиять на характер получаемых решений (например, при определенных условиях может привести к неустойчивости решений).
6

I.МЕТОД ШАГОВ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
СЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ
ГЛАВА I. Метод шагов решения дифференциальных уравнений
сзапаздывающим аргументом
1.1.Классификация дифференциальных уравнений с отклоняющимся аргументом. Постановка начальной задачи
Определение 1. Дифференциальными уравнениями с отклоняющимся аргументом называются дифференциальные уравнения, в которых неизвестная функция X(t) входит при различных значениях аргумента.
Примеры:
.
X(t) = f {t, x(t), x[t - τ(t)]},
. |
|
|
|
|
X(t) = f [t, x(t), x(t - τ1 ), x(t −τ2 )], |
||||
.. |
|
. |
|
. |
X(t) = f t, x(t), x(t), x[t -τ(t)], x[t −τ |
||||
|
|
|
|
|
.. |
|
. |
. |
|
X(t) = f t, x(t), x(t), x(t/2), x(t/2) . |
||||
|
|
|
|
|
|
|
(1) |
|
|
(2) |
(t)] |
, |
(3) |
|
|
|
|
|
(4) |
Определение 2. Дифференциальным уравнением с запаздывающим аргументом называется дифференциальное уравнение с отклоняющимся аргументом, в котором производная наивысшего порядка от неизвестной функции входит при одинаковых значениях аргумента и этот аргумент не меньше, чем все аргументы неизвестной функции и ее производных, входящих в уравнение.
Заметим, что согласно определению 2, уравнения (1) и (3) при условиях τ(t) ≥ 0 , t −τ(t) ≥ 0 будут уравнениями с запаздывающим аргументом, уравнение (2) будет уравне-
нием с запаздывающим аргументом, если τ1 ≥ 0 , τ2 ≥ 0 , t ≥τ1 , t ≥τ2 , уравнение (4) есть уравнение с запаздывающим аргументом, так как t ≥ 0 .
Определение 3. Дифференциальным уравнением с опережающим аргументом называется дифференциальное уравнение с отклоняющимся аргументом, в котором производная наивысшего порядка от неизвестной функции входит при одинаковых значениях аргумента и этот аргумент не больше остальных аргументов неизвестной функции и ее производных, входящих в уравнение.
Примеры дифференциальных уравнений с опережающим аргументом:
.
X (t) =
.
X (t) =
..
X (t) =
f {t, x(t), x[t +τ(t)]},
f [t, x(t), x(t +τ1 ), x(t +τ2 )],
ft, x(t), x. (t), x[t +τ(t)], x. [t +τ
|
(5) |
|
(6) |
(t)] . |
(7) |
|
|
7
I.МЕТОД ШАГОВ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
СЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ
Определение 4. Дифференциальные уравнения с отклоняющимся аргументом, не являющиеся уравнениями с запаздывающим или опережающим аргументом называются дифференциальными уравнениями нейтрального типа.
Примеры дифференциальных уравнений с отклоняющимся аргументом нейтрального типа:
X (t)= f t, x(t), x(t −τ), x(t −τ) |
, |
(8) |
|
. |
. |
|
|
|
|
|
|
|
|
|
|
X (t)= f t, x(t), x[t −τ(t)], x[t −τ(t)], x[t −τ(t)] . |
(9) |
||
.. |
. |
.. |
|
|
|
|
|
Отметим, что аналогичная классификация применяется и для систем дифференциальных уравнений с отклоняющимся аргументом заменой слова "функция" словом "вектор функция".
Рассмотрим простейшее дифференциальное уравнение с отклоняющимся аргументом:
. |
(10) |
X (t)= f [t, x(t), x(t −τ)], |
где τ ≥ 0 и t −τ ≥ 0 (фактически рассматриваем дифференциальное уравнение с запаздывающим аргументом). Основная начальная задача при решении уравнения (10) заключается в следующем: определить непрерывное решение X (t) уравнения (10) для t > t0 (t0 –
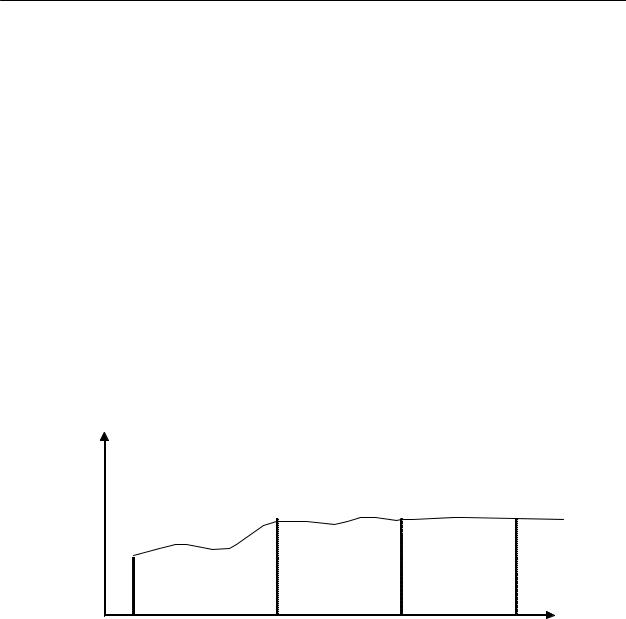
фиксированное время) при условии, что X (t)=ϕ0(t), когда t0 −τ ≤ t ≤ t0 , где ϕ0(t) – заданная непрерывная начальная функция. Сегмент [t0 − τ, t0]называется начальным множеством, t0 называется начальной точкой. Предполагается, что X (t0 + 0)=ϕ0(t0 ) (рис. 1).
X(t)
X (t )=ϕ0(t)
0 |
t0 −τ |
t0 |
t0 +τ |
t |
0 + τ |
t |
|
|
|
|
2 |
|
|
|
|
|
Рис. 1. |
|
|
|
Если запаздывание τ |
в уравнении (10) зависит от времени t |
(τ =τ(t )), то началь- |
||||
ная задача ставится следующим образом: найти решение уравнения (10) при t > t0 , если известна начальная функция X (t)=ϕ0 t при t0 − τ(t0 )≤ t ≤ t0 .
Пример. Найти решение уравнения.
. |
(11) |
|
X (t)= f [t, x(t), x(t −cos2 t)] |
|
|
при t > t0 = 0 , если начальная функция X (t)=ϕ0(t) при (t0 −cos2 t0 ) | |
t ≤t0 |
| (или |
t0 =0 |
t0 |
=0 |
−1 ≤ t ≤ 0 ).
8

I.МЕТОД ШАГОВ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
СЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ
Пример. Найти решение уравнения
|
. |
|
|
|
|
|
(12) |
|
|
при |
X (t)= f [t, x(t), x(t / 2)] |
|
|
при (t |
−t |
/ 2) | |
|
| (или |
|
t > t0 =1 , если начальная функция X (t)= ϕ t |
≤t ≤t |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
t =1 |
|
0 |
t =1 |
|
|
|
|
|
|
0 |
|
|
0 |
1/ 2 ≤ t ≤1).
Отметим, что начальная функция обычно задается или находится экспериментально (в основном в технических задачах).
1.2. Дифференциальные уравнения с запаздывающим аргументом. Метод шагов
Рассмотрим дифференциальное уравнение с запаздывающим аргументом.
. |
|
(13) |
X (t)= f [t, x(t), x(t −τ)], |
|
|
где τ ≥ 0 , t −τ ≥ 0 , с заданной начальной функцией X (t)=ϕ0 t |
при t0 −τ ≤ t ≤ t0 . |
|
|
|
|
|
|
|
Требуется найти решение уравнения (13) при t ≥ t0 .
Для нахождения решения уравнения (13) при t ≥ t0 будем пользоваться методом шагов (метод последовательного интегрирования).
Суть метода шагов состоит в том, что сначала найдем решение уравнения (13) для t0 ≤ t ≤ t0 + τ , потом для t0 +τ ≤ t ≤ t0 +2τ и т.д. При этом заметим, например, что так как в области t0 ≤ t ≤ t0 + τ аргумент t − τ меняется в пределах t0 −τ ≤ t −τ ≤ t0 , то в уравнении
(13) в данной области вместо x(t −τ) можно взять начальную функцию ϕ0(t −τ). Тогда
получим, что для нахождения решения уравнения (13) в области t0 ≤ t ≤ t0 |
+ τ нужно ре- |
|
шить обыкновенное дифференциальное уравнение без запаздывания в виде: |
|
|
. |
[t, x(t),ϕ0(t −τ)], |
(14) |
X (t)= f |
||
при t0 ≤ t ≤ t0 + τ |
с начальным условием X (t0)=ϕ(t0) (см. рис. 1). |
|
Теперь, |
найдя решение этой начальной задачи в виде X (t)=ϕ1 (t), |
можем поста- |
вить задачу нахождения решения на отрезке t0 +τ ≤ t ≤ t0 +2τ и т.д.
Итак имеем:
|
. |
|
0 (t −τ)], |
|
|
X (t)= f [t, x(t),ϕ |
(15) |
||
при t0 |
≤ t ≤ t0 + τ , X (t0 ) |
= ϕ0 (t0 ), |
|
|
|
. |
|
|
|
|
X (t)= f [t, x(t),ϕ1(t −τ)], |
(16) |
||
при t0 +τ ≤ t ≤ t0 + 2τ , |
X (t0 +τ)= ϕ1(t0 +τ), |
|
||
|
. |
|
|
|
|
X (t)= f [t, x(t),ϕ2 (t −τ)], |
(17) |
||
при t0 + 2τ ≤ t ≤ t0 +3τ , |
X (t0 + 2τ)= ϕ2 (t0 + 2τ), |
|
||
|
. |
|
|
|
|
X (t)= f [t, x(t),ϕn (t −τ)], |
(18) |
||
при t0 + nτ ≤ t ≤ t0 + (n +1)τ , X (t0 + nτ)= ϕn (t0 + nτ), |
|
|||
где |
ϕi(t) есть |
решение рассматриваемой начальной |
задачи на отрезке |
|
t0 + (i −1)τ ≤ t ≤ t0 +iτ |
(I=1,2,3…n,…). |
|
||
9

I.МЕТОД ШАГОВ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
СЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ
Такой метод шагов решения дифференциального уравнения с запаздывающим аргументом (13) позволяет определить решение X (t) на некотором конечном отрезке изменения t.
Пример 1. Методом шагов найти решение дифференциального уравнения 1-го порядка с запаздывающим аргументом
. |
(t)= 6 X (t −1) |
|
|
(19) |
X |
|
|
||
в области 1 ≤ t ≤ 3 , если начальная функция при 0 ≤ t ≤1 имеет вид X (t)= ϕ0 (t)= t . |
||||
Решение. Сначала найдем решение уравнения (19) в области 1 ≤ t ≤ 2 . Для этого в |
||||
(19) заменим X (t −1) на ϕ0(t −1), т.е. |
|
|||
X (t −1)=ϕ0 (t −1)= t|t→t −1 = t −1 |
|
|||
и учтем X (1)= ϕ0 (1)= t| |
=1 |
=1 . |
(20) |
|
|
t |
|
|
|
Итак в области 1 ≤ t ≤ 2 получим обыкновенное дифференциальное уравнение вида |
||||
. |
(t)= 6 (t −1) |
|
|
(21) |
X |
|
|
||
или dx(t) |
= 6(t −1). |
|
|
|
dt |
|
|
|
|
Решая его с учетом (20), получим решение уравнения (19) при 1 ≤ t ≤ 2 в виде |
||||
X (t)= 3t 2 −6t +4 = 3(t −1)2 +1. |
(22) |
|||
Для нахождения решения в области 2 ≤ t ≤ 3 в уравнении (19) заменим X (t −1) на |
||||
ϕ1(t −1)= 3(t −1)2 +1|t→t−1 |
= 3(t −2)2 +1. Тогда получим обыкновенное |
дифференциальное |
||
уравнение: |
|
|
|
|
. |
(t)= 6[3(t −2)2 +1], X (2)=ϕ1 (2)= 4 , |
|
||
X |
|
|||
решение которого имеет вид (Рис. 2) |
|
|||
X (t)= 6(t − 2)3 + 6t −8 . |
(23) |
|||
X(t)
4
3
2
1
0 1 2 |
t |
Рис. 2
10
