6.7 Обыкновенные дифференциальные уравнения

Задача Коши для дифференциального уравнения первого порядка

Задача Коши для дифференциального уравнения первого порядка включает уравнение вида:

и начальное условие: .

Существуют различные методы численного решения задачи Коши: методы рядов Тейлора, одношаговые методы Рунге-Кутта, многошаговые разностные методы. При решении уравнения численными методами значения функции находятся приближенно в виде дискретной числовой последовательности {y_i}, где .

Методы Рунге-Кутта.

Простейшим вариантом методов Рунге-Кутта является метод Эйлера, при котором производная заменяется конечной разностью.

В случае ,, тогда,

где ,,,.

Данный метод имеет первый порядок точности по h, погрешность нарастает с удалением от точки . Метод Эйлера является методом Рунге-Кутта первого порядка.

Общий вид методов Рунге-Кутта (при ) записывается с помощью формулы:

, где  порядок метода, ,

,

,

,

. . . . . . . . ,

.

Коэффициенты ,,выбираются из соображений точности.

Метод Эйлера получается при .

Для имеется уже семейство методов Рунге-Кутта второго порядка, для которых должно выполнятся условие.

В частности при иполучается, так называемый,исправленный метод Эйлера:

.

При ,,, получаетсямодифицированный метод Эйлера:

.

Большое распространение получили методы Рунге-Кутта четвертого () порядка точности. Ниже приведены примеры методов четвертого порядка:

Пример 1.

, ,

, ,

.

Пример 2.

, ,

, ,

.

Для повышения точности вычислений можно воспользоваться итерационным методом уточнения. Он заключается в том, что каждое значение вычисляется с помощью последовательных приближений. Например, для метода Эйлера за начальное приближение берется, найденное значение уточняется по формуле, где

Уточнение продолжают до тех пор, пока в пределах требуемой точности два последовательных приближения не совпадут.

Задача Коши для дифференциального уравнения n-го порядка.

Каноническая форма обыкновенного дифференциального уравнения n-го порядка имеет вид: . Начальные условия для задачи Коши:

.

Уравнение порядка n сводится к эквивалентной системе n уравнений первого порядка путем замены переменных:

. Задача Коши сводится к решению системы n уравнений с начальными условиями: 

 

 

Для ее решения применимы те же методы, о которых говорилось выше. Численное решение этой задачи состоит в построении таблицы приближенных значений y_i, y_1,i, y_2,i,…, y_n-1,i, i=1,2,…,k решения u(x) и его производных: u₁(x),…, u_n-1(x) на отрезке [ x₀, x_k] в точках x₀,x₁,…,x_k.

Например, дано уравнение 2-го порядка , удовлетворяющее начальным условиям,. Введение дополнительной функциисводит задачу к эквивалентной системе двух уравнений с начальными условиями

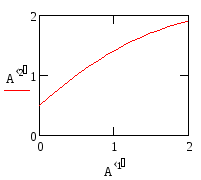
Ниже показано решение этой задачи с помощью встроенной в MathCAD функции rkfixed. Здесь вектор-функция {u(x), u₁(x)} обозначена как {y₁(x), y₂(x)}. При вычислении решения на отрезке , на сетке с 15-ю равноотстоящими узлами получается:

Функция rkfixed имеет пятьаргументов. Первый аргумент  вектор начальныхусловий. Два вторых аргумента задают начальное и конечное значение x. Четвертый определяет количество шагов интегрирования. Последний аргумент  это вектор-функция, составленный из правых частей системы уравнений. Результатом вычислений является матрица, первый столбец которой задает координату х, следующие столбцы соответственно y, y’…