3

ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Лабораторная работа № 4

Параллельное соединение активного и реактивного элементов

(исследование разветвленной цепи переменного тока)

Ответы на вопросы

1. По каким формулам определяется активная и реактивная проводимости ветвей?

2. Что такое емкостное сопротивление и как оно определяется?

3. Какой режим цепи при параллельном соединении элементов называется резонансом токов?

Перечень приборов

1. Источник энергии переменного тока – 30 В

2. Реостат – 1 шт.

3. Мультиметр – 3 шт.

4. Ваттметр – 1 шт. (0 –1200 Вт)

5. Катушка индуктивности – 1 шт.

6. Магазин сопротивлений – 1 шт. (R = 410 Ом)

7. Магазин емкостей – 1 шт. (С = 121 мкф)

Краткие теоретические сведения

Резонансом токов называют такой режим работы разветвленной электрической цепи, состоящей включенных параллельно катушки индуктивности и конденсатора, при которых реактивные проводимости элементов становятся равными:

B_L = B_C

где B_L = 1/ωL – реактивная проводимость катушки;

B_С = ωС – реактивная проводимость конденсатора.

Равенство реактивных проводимостей может быть достигнута изменением емкости, индуктивности или частоты напряжения питания. В данной работе резонанс токов достигается изменением емкости.

Действующее значение тока в электрической схеме (рис. 3) определяется выражением:

I = UY = U√G² + (B_L – B_C)²

где U – напряжение питания схемы;

Y – полная проводимость схемы;

G – активная проводимость схемы;

B_L и B_C – реактивные проводимости элементов схемы.

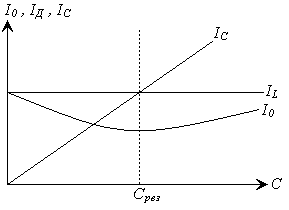
При плавном увеличении емкости (от минимального значения) к моменту, когда ее значение становится близким к резонансному, ток емкостной ветви увеличивается и стремится к равенству с током катушки индуктивности.

Общий ток схемы непрерывно уменьшается и при резонансе становится минимальным, так как реактивная проводимость схемы равна нулю и действует лишь активная проводимость:

I = UY = U√G² + (B_L – B_C)² = UG

Дальнейшее изменение приводит к росту общего тока и тока в ветви, где включен конденсатор (рис. 1).

Рис. 1 Графики зависимости общего тока и токов, протекающих через катушку индуктивности и конденсатор от величины емкости.

Следует отметить, что в рассматриваемой разветвленной цепи, токи в ветвях с реактивными элементами могут превышать общий ток до разветвления.

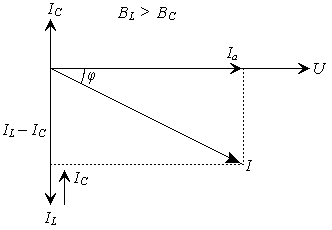
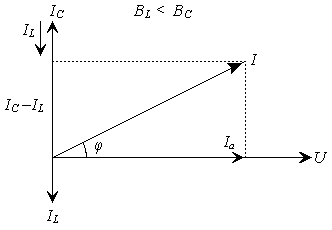
При B_L > B_C (I_L > I_C) электрическая цепь имеет индуктивный характер; при B_L > B_C (I_L < I_C) электрическая цепь имеет емкостной характер; при резонансе токов B_L = B_C (I_L = I_C) и cos φ = 1. Векторные диаграммы для этих случаев представлены на рис. 2.

Рис. 2 Векторная диаграмма для электрической цепи при параллельном включении катушки индуктивности и конденсатора

План работы

1. Определить размещение приборов на столе.

2. Собрать электрическую схему цепи (рис. 3).

3. Предъявить собранную схему для проверки.

4. Включить автомат переменного тока, установить с помощью реостата заданное напряжение U и удерживать его в течении опыта постоянным.

5. С помощью приборов измерить все необходимые для расчетов величины.

6. Записать показания амперметра, вольтметра и ваттметра в таблицу № 1.

7. По измеренным и вычисленным данным для трех режимов, построить векторные диаграммы напряжений. Диаграммы строить на миллиметровой бумаге в масштабе.

Масштаб напряжения М_U = В/см

Масштаб тока М_I = А/см

Расчетные формулы

Сделать вывод.

Таблица № 1

Участок цепи

U

I

P

R

Z

X

IA

IP

S

Q

sinφ

cosφ

φ

В

А

Вт

Ом

Ом

Ом

А

А

В

Вар

град

Резистор

Х

Катушка

Х

Х

Конденсатор

Х

Х

Х

Вся цепь

Х

Х

Х

Х

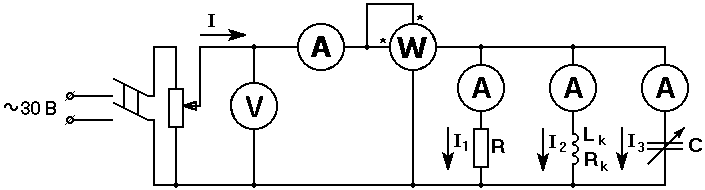
Рис. 3 Электрическая схема с катушкой индуктивности, конденсатором и сопротивлением, включенными параллельно.