Алгебра логики - булева алгебра
итехническая реализация процесса вычисления.
Булева алгебра (основные понятия)
Алгебра (или алгебра логики). В ней логические выражения принимают только два значения:
ИСТИНА - 1 или ЛОЖЬ - 0
Логические выражения являются функциями логических переменных: A, B, C ..., каждая из которых принимает значение 0 или 1.
Булева алгебра (основные понятия)
Любая функция логических переменных может быть образована посредством 3-х основных логических операций:
Логическое И - *
Логическое ИЛИ - +.
Логическое НЕ - .
Таблица основных логических 
операций
А |
B |
F= |
|
|
F= |
|
|
F=A B |
F=AB |
А |
B |
||||||||
0 |
0 |
1 |
|
1 |
|
0 |
0 |
||
0 |
1 |
1 |
|
0 |
|
1 |
0 |
||
1 |
0 |
0 |
|
1 |
|
1 |
0 |
||
1 |
1 |
0 |
|
0 |
|
1 |
1 |
||
Алгебраические выражения.
А к с |
и |
о |
м |
ы |
и |
|
з |
а к о |
н |
ы |
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
л |
г |
е |
б |
р |
а |
и |
ч |
е |
с к |
и |
е |
в |
ы |
р а |
ж |
е |
н и |
я |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
б у л е |
|
в |
о й |
а |
л |
г |
е б |
р ы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А к с и |
о м |
ы |
|
( т |
о |
ж |
д е |
с т |
в а ) |
|
1 |
|
A |
|
1 |
|
|
0 |
|
|
A |
|
A |
|
|
|
|
|
|
|
|
|
|
|
A |
|
A |
|
|
A |
|
|
|
|
|
|
|
|
|
A |
|
|
|
A |
|
1 |
|
|
|
A |
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
A |
|
0 |
|
|
1 |
|
A |
|
A |
|
|
|
|
|
|
|
|
|
|
|
A |
|
A |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З а |
к о |
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
A |
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
B |
|
|
|
B |
|
|
|
|
A |
|
и |
л |
и |
|
|
A |
|
B |
|
|
|
B |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|||||||
к о м |
м |
|
у |
т |
а т |
и |
в |
н о с т |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
З а |
к о |
н |
|
|
|
|
|
|
|
|
|
|
A |
B |
|
|
С |
|
A |
|
|
|
( B |
|
|
|
С |
|
) |
|
|
и |
л |
и |
A |
|
|
B |
|
|
C |
|
|
|
|
|
A |
|
( B |
C |
) |
|
|
|
||||||
а с с |
о |
|
ц |
и а |
т и |
в |
н |
о с |
т и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
З а |
к о |
н |
|
|
|
|
|
|
|
|
A |
( B |
С |
) |
( |
A |
|
|
B |
) |
( |
A |
|
|
|
|
С |
|
|
) |
|
|
и |
л |
и |
|
A |
|
|
|
( B |
|
|
C |
) |
|
|
( |
A |
|
B ) |
( A |
C |
) |
||||||
д и с |
т р |
и |
б |
у т |
и |
в |
н о |
с т |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
З а к |
о |
н |
|
д |
у а |
л |
ь |
н о с т |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(т |
е |
о |
р е |
м |
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
л |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Д |
е |
н а ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
B |
|
|
A |
|
|
|
B |
|
|
|
|
A |
|
B |
|
A |
|
|
|
B |
|
|
|
|
|
|
|
|||||||||||||||||||
|
' М |
|
о р |
г |
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
З а к |
о н |
|
|
п о |
г л |
о |
щ |
е |
н и |
я |
|
|
|
|
|
|
|
|
|
|
A |
|
A |
|
B |
|
|
|
|
A |
|
|
|
и |
л |
и |
|
A |
( |
A |
|
|
B |
|
) |
|
|
|
A |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Применение |
|
этих законов и аксиом позволяет упростить |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
логические функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
A A B по закону дистрибутивности (A A) (A B) A B
Таблицы истинности
Булевы выражения - это удобный инструмент для описания принципа работы логической схемы.
Другой точный метод описания того, как работает логическая схема - таблица
истинности.
Можно легко преобразовать информацию из таблицы истинности в логическое выражение и обратно.
Таблицы истинности
A B C 1
A B C A B C Y
A B C 1
Только 2 из 8 комбинаций дают 1. Эти две комбинации
|
|
|
|
|
|
связаны логической |
A |
B C или A B |
C |
||||
функцией 'ИЛИ' (+) |
|
|||||
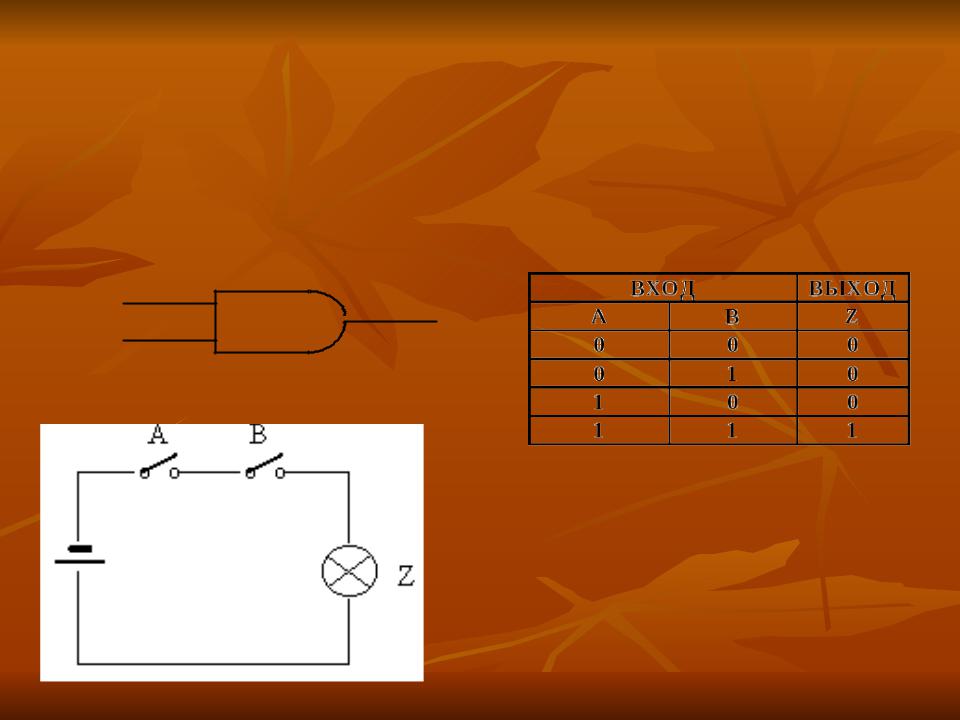
Простейшие логические
элементы
Элемент AND -И
Таблица истинности
Вход |
A |
|
Z |
|
|
Z=A*B |
|
|
|
Выход |
|
Вход |
B |
|
|
|
|
Лампочка загорится, когда оба ключа включены:A 'И'. B
Простейшие логические
Элемент OR - ИЛИ элементы
Таблица истинности
Лампочка загорится, когда оба ключа включены:A 'И'. B
Простейшие логические
элементы
Элемент NOT - НЕ (инвертор)
Таблица истинности
Сигнал на выходе всегда противоположен сигналу на входе