
Лабораторная работа № 4
Переходный процесс при несимметричном коротком замыкании в электрической сети, питающейся от источника практически бесконечной мощности
Продолжительность работы: 4 часа.
Цель работы: Изучение переходного процесса в электрической сети при нессиметричном коротком замыкании.
Программа изучения переходных процессов при несимметричном коротком замыкании:
-
Ознакомиться с теоретической частью.
-
Ознакомиться с конструкцией стенда.
-
Ознакомится с порядком выполнения работы.
-
Собрать схему лабораторной работы согласно указаниям.
-
Провести необходимые испытания.
-
Составить отчет по проделанной работе.
Краткие теоретические сведения:
Несимметричные переходные процессы в электрических системах
Несимметричные режимы возникают вследствие несимметричных коротких замыканий или обрыва одной-двух фаз линии. В первом случае в электрической сети появляется поперечная несимметрия, во втором – продольная. Строгий математический анализ переходных процессов при несимметрии затруднён тем, что в электрических машинах возникает пульсирующее магнитное поле ротора, которое образует полный спектр высших гармонических составляющих тока. Замена координатных осей А, В, С на систему d, q, 0 не освобождает дифференциальные уравнения от периодических коэффициентов. Поэтому в большинстве практических расчётов учитывается лишь основная гармоника токов или напряжений. Только при таком ограничении возможно использование метода симметричных составляющих, который наиболее часто применяется для анализа несимметричных КЗ [2, глава 6].
Метод симметричных составляющих
Метод симметричных составляющих базируется на математической теории многофазных электрических систем при неодинаковых условиях работы фаз. Математическое обоснование метода было разработано К. Фортескью (С. L. Fortescue), а затем Р. Эвансом и К. Вагнером (R. Evans и С. Wagner), которые применили его для решения задач, возникающих при анализе несимметричных КЗ.
Сформулируем основные положения метода симметричных составляющих.
1. Любую несимметричную систему токов можно разложить на три симметричные, называемые системами прямой, обратной и нулевой последовательностей. Эти системы получили название «симметричные составляющие». Предполагается, что они одновременно циркулируют в рассматриваемой сети в несимметричном режиме.
Симметричная система токов прямой
последовательности (рис. 1.42, а) представляет
собой три одинаковых по величине вектора,
расположенных под углом 120°, вращающихся
против часовой стрелки так, что соблюдается
нормальное чередование фаз: А – В
– С. Соотношения между фазными
значениями устанавливаются с помощью
оператора
![]()

Рис. 4.1. Система токов прямой (а), обратной (б) и нулевой (в) последовательностей.
Любой из трёх одинаковых векторов единичной длины имеет аргумент, равный 120°. Если некоторый вектор, например IА1 , умножить на a , то это означает повернуть IА1 на 120° против часовой стрелки. С помощью оператора a можно выразить токи фаз В и С через ток фазы А:
![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
Симметричная система токов обратной последовательности (рис. 4.1, б) представляет собой три одинаковых по величине вектора, расположенных под углом 120° и вращающихся против часовой стрёлки так, что соблюдается обратное чередование фаз: А–С–В. При этом токи фаз В и С связаны с током фазы А следующим образом:
![]() (4.3)
(4.3)
![]() (4.4)
(4.4)
Симметричная система токов нулевой последовательности (рис. 4.2, в) существенно отличается от прямой и обратной. Она представляет собой систему трёх переменных токов, совпадающих по фазе и имеющих одинаковую амплитуду. Эти токи являются, по существу, разветвлением однофазного тока, для которого три провода трёхфазной цепи составляют один прямой провод, а обратным служит земля или четвертый (нулевой) провод. Появление токов нулевой последовательности в сети означает возникновение в ней несимметричного замыкания на землю. Рассматриваемая несимметричная система токов допускает только одно разложение на симметричные составляющие. Действительно, представив ток каждой фазы через его симметричные составляющие, получим:
![]() (4.5)
(4.5)
![]() (4.6)
(4.6)
![]() (4.7)
(4.7)
Если IА , IВ
, IС заданы, то
искомыми являются три величины
![]() .
Они определяются тремя линейными
уравнениями, которые допускают только
одно решение:
.
Они определяются тремя линейными
уравнениями, которые допускают только
одно решение:
![]() (4.8)
(4.8)
![]() (4.9)
(4.9)
![]() (4.10)
(4.10)
Все соотношения для симметричных составляющих токов справедливы и для напряжений.
Рассмотрим разложение на составляющие несимметричной системы токов (рис. 4.2, а).

Рис. 4.2. Разложение несимметричной системы токов на симметричные составляющие
С помощью геометрических построений, соответствующих выражениям (4.8) – (4.10), найдём ток нулевой, прямой и обратной последовательностей (рис. 4.2, б–г). Если сложить симметричные составляющие в соответствии с выражениями (4.5) – (4.7), то получим исходную систему.
2. В трёхфазной цепи в месте КЗ наряду с напряжениями прямой последовательности возникают напряжения обратной и нулевой последовательностей. В ветвях схемы вместе с токами прямой последовательности начинают циркулировать токи обратной и нулевой последовательностей.
3. В симметричных электрических системах токи и напряжения схем отдельных последовательностей могут рассматриваться независимо друг от друга и быть связаны между собой законами Ома и Кирхгофа.
Если какой-либо элемент цепи симметричен и при протекании по нему токов I1, I2, I0 обладает некоторыми сопротивлениями Z1 , Z2 , Z0 , то симметричные составляющие падения напряжения в этом элементе будут равны
![]() (4.14)
(4.14)
4. Элементы трёхфазной сети для токов прямой, обратной и нулевой последовательностей имеют неодинаковые сопротивления. ЭДС генераторов симметричны, т.е. не содержат обратной и нулевой составляющих. Отсюда следует, что:
а) в электрических системах существуют только ЭДС прямой последовательности;
б) токи обратной и нулевой последовательностей определяются только напряжениями в точке КЗ.
5. Между системами трёх симметричных составляющих всегда существует связь, задаваемая условиями короткого замыкания. Эта связь легко устанавливается путём перевода граничных условий короткого замыкания, заданных через действительные токи и напряжения, в условия, заданные через симметричные составляющие.
Подробнее с теорией о методе симметричных составляющих можно ознакомится, используя пособия указанные в списке литературы [2, глава 6].
Однократная поперечная несимметрия
Рассмотрим три вида несимметричных КЗ: однофазное, двухфазное и двухфазное на землю. Токи и напряжения в месте КЗ определяют с учётом граничных условий в этом месте. При их записи принимается, что фаза А находится в условиях, отличных от условий для фаз В и С, т.е. является особой фазой. Выражения для токов получены при условии, что короткие замыкания – металлические. [3, раздел 1] Учёт сопротивления дуги не приводится.
Однофазное короткое замыкание
Граничные условия в месте КЗ (рис.4.6):
![]() (4.18)
(4.18)
![]() (4.19)
(4.19)
![]() (4.20)
(4.20)

Рис. 4.6. Токи в месте однофазного КЗ
В дальнейшем индекс вида КЗ опускаем. Условия (4.19) и (4.20) позволяют получить следующие соотношения токов различных последовательностей (с учётом(4.8)–(4.10):
![]() (4.21)
(4.21)
С учётом (4.18) напряжение фазы А в месте КЗ будет равно:
![]() (4.22)
(4.22)
Подставляя в (4.22) выражения для напряжений различных последовательностей и учитывая (4.21), получим:
![]()
![]()
откуда выражение для тока прямой последовательности будет иметь вид:
![]() (4.23)
(4.23)
Входящие в это выражение результирующие
ЭДС EА∑ и сопротивления
![]() определяются относительно начала и
конца схемы. Преобразования схем прямой,
обратной и нулевой последовательностей
позволяют получить эквивалентные схемы.
определяются относительно начала и
конца схемы. Преобразования схем прямой,
обратной и нулевой последовательностей
позволяют получить эквивалентные схемы.
Зная ток прямой последовательности, определяем полный ток в повреждённой фазе:
![]() (4.24)
(4.24)
Симметричные составляющие напряжений в месте КЗ вычисляются по формулам:
![]()
![]()
![]() ,
,
а напряжения фаз В и С в месте КЗ – по формулам:
![]()
![]()
Векторные диаграммы напряжений и токов в месте КЗ показаны на рис. 1.54.

Рис. 4.7. Векторные диаграммы напряжений (а), токов (б) в месте однофазного КЗ
Двухфазное короткое замыкание
Граничные условия в месте КЗ (рис. 1.55) имеют вид
![]()
![]() (4.25)
(4.25)
![]()

Рис. 4.8. Токи в месте двухфазного КЗ
Поскольку место КЗ не связано с землей и нет пути для протекания тока нулевой последовательности, условие (4.25) можно записать в виде
IКA = IКA1 + IКA2 = 0. IКA1 = -IКA2. (4.26)
Выразим напряжения повреждённых фаз через симметричные составляющие напряжения фазы А и с учётом (4.26) получим:
![]()
Так как (a2 - a)
![]() 0
, то U КA1 =U
КA2 .
0
, то U КA1 =U
КA2 .
Это равенство позволяет приравнять правые части,
т.е. EА∑- jx 1∑IКА=- jx 2∑ I КА2, откуда, учитывая (4.26), получим:
![]()
Токи повреждённых фаз в месте КЗ
вычисляются с учетом значения
![]() .
.
Напряжения повреждённых фаз в месте КЗ определяются по формулам
![]()
![]()

Рис. 4.9. Векторные диаграммы напряжений (а) и токов (б) в месте двухфазного КЗ
Двухфазное короткое замыкание на землю
Граничные условия в месте КЗ (рис. 1.57) имеют вид
![]()
![]() (4.27)
(4.27)
![]()
эти условия можно записать в ином виде:
![]()

Рис. 4.10. Токи в месте двухфазного КЗ на землю
Условия (4.27) позволяют записать соотношение:
![]()
 (4.28)
(4.28)
Токи повреждённых фаз в месте КЗ
определяются с учетом значения
![]()
Ток в земле вычисляется по формуле:
![]() (4.29)
(4.29)
Векторные диаграммы напряжений и токов в месте КЗ показана на рис. 4.11.
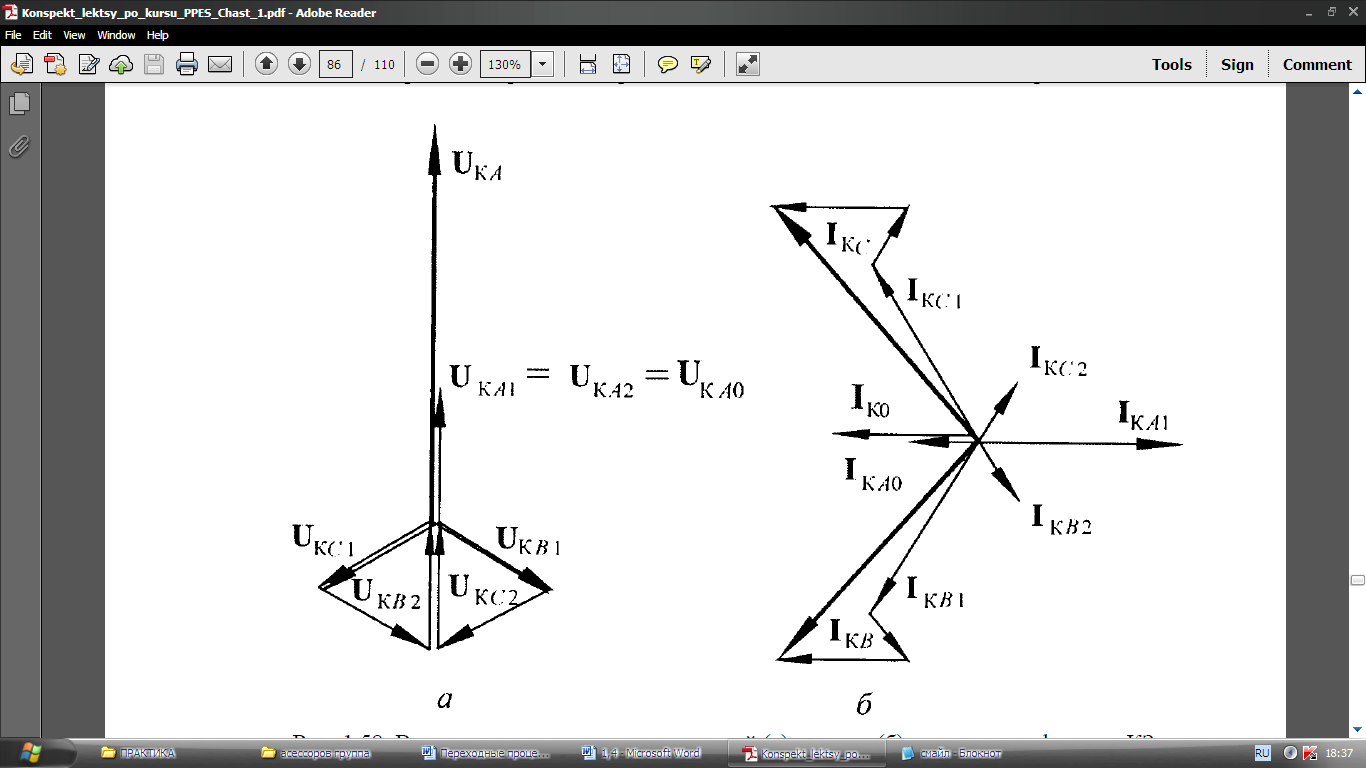
Рис. 4.11. Векторные диаграммы напряжений (а) и токов (б) в месте двухфазного КЗ на
Землю
Данные для выполнения работы:

![]()
![]()

