19

2. Элементы теории множеств

1. . Основные понятия

Под множеством обычно понимают некоторый набор (совокупность) элементов произвольной природы. Например, совокупность короткозамкнутых асинхронных двигателей серии 4A, набор сопротивлений и т.д. Множества вещественных, натуральных и целых чисел являются примером числовых множеств.

Каждый из таких элементов в отдельности есть элемент множества. Фразу «е является элементом множества Е» («е принадлежит множеству Е») записывают, кратко в виде еЕ. Если е не принадлежит множеству Е, то пишут е Е.

Пусть a, b, c… – элементы множества E. Используя фигурные или круглые скобки можно записать

E = {a, b, c,...} = (a, b, c,...).

Если элементы множества E суть все целые числа от k до l (kl), то для обозначения e можно использовать более простую запись:

e = {k, k+1,..., l–1, l} = k:l.

Например, множество натуральных чисел от 1 до n можно записать так:

{1, 2, ..., n} = 1:n.

Элементы множества могут быть пронумерованы или каждому элементу множества может быть прописан некоторый индекс, причем так, что все элементы имеют разные индексы. Например, E = {e₁, e₂, ..., e_n}. Используя обозначение 1:n, множество E запишем в виде:

E = e[1:n],

где e_i = e[i] – элемент множества E.

Если множество E состоит из элементов e, обладающих определенным свойством P(e), то пишут E = {eP(e)}.Например (0, 1] = {e0 x 1}. Для указания множества E₁, элементы e которого принадлежат E₂ и, кроме того, обладают свойством P(e), используют обозначение:

E₁ = {eE₂P(e)}.

Множество можно изобразить кругом Эйлера – считать его множеством точек, ограниченных окружностью: на рис. 2.1 показано включение eE.

Рис. 2.1. Включение е в E Рис. 2.2. Включение подмножества

Ē в множество Е

Множество Ē представляет собой некоторое подмножество множества E (Ē  E), если каждый элемент e, принадлежащий Ē, одновременно принадлежит и E. (рис. 2.2). В случае, когда Ē не содержит ни одного элемента (т.е. является пустым множеством, Ē = Ø), оно может рассматриваться как подмножество любого множества. Ē является истинным или собственным подмножеством E при условиях Ē  Ø, Ē  E (обозначается Ē E).

Знаки « », « » называют знаками включения (соответственно строго и не строго) одного множества в другое. Равенство E₁ = E₂ имеет место тогда и только тогда, когда одновременно E₁E₂ и E₂E₁, т.е. состоят из одних и тех же элементов.

Пересечение множеств E₁ и E₂ (E₁E₂) есть множество всех элементов e, содержащихся в E₁ и в E₂ (рис. 2.3, а). Множества E₁ и E₂ являются непересекающимися, если E₁E₂ = Ø. Например, множества малых и больших ЭВМ вычислительного центра.

Операция пересечения множеств обладает сведущими свойствами:

1⁰) E₁E₂ = E₂E₁,

2⁰) (E₁E₂)E₃ = E₁(E₂E₃),

3⁰) E₁E₁=E₁; E₁ Ø = Ø,

где E₁, E₂, E₃ – произвольные множества.

Объединение множеств E₁ и E₂ (E₁E₂) есть множество всех элементов e, содержащихся либо в E₁, либо в E₂, либо и в E₁ и в E₂ (рис. 2.3, б), т.е. в объединении находятся элементы, принадлежащие E₁, E₂ и обоим множествам вместе. Операция объединения множеств обладает следующими свойствами:

1⁰) E₁E₂ = E₂E₁,

2⁰) (E₁E₂)E₃ = E₁(E₂E₃),

3⁰) E₁E₁ = E₁; E₁ Ø = E₁.

Разностью множеств E₁ и E₂ называют множество, состоящее из элементов, которые принадлежат множеству E₁, но не принадлежат множеству E₂ (E₁\E₂) т.е. совокупность всех eE₁, таких что eE₂ (рис. 2.3, в).

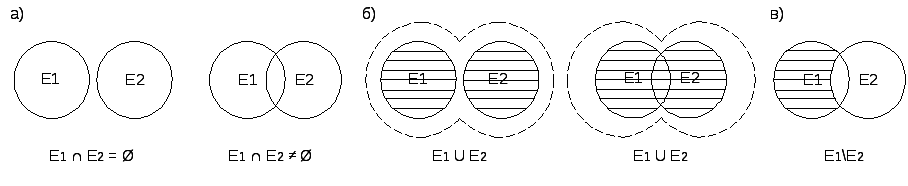
Рис. 2.3. Пересечение (а), объединение (б), разность (в) множеств

Если E₂ – одноэлементное множество, т.е. E₂ = {e}, то E₁\{e} будем записывать и проще: E₁–e. Число элементов во множестве E₁ (обозначается E₁ = e) называется мощностью конечного множества. Для бесконечного множества E₂ мощность считается равной бесконечности (E₂ = ∞).

Отношением, существующем на множестве E, называется форма связи между элементами или подмножествами этого множества. Отношения определяются словами («быть меньше, чем ...», «обладать свойствами делимости на ...», «быть одинаковым с ...») или символами(«=», « », «»).

Важнейшую роль играет отношение «быть функцией». Говорят, что на множестве E задана функция f со значениями во множестве Э, если каждому элементу eE сопоставлен элемент эЭ (обозначается э = f(e)). Если при этом из e₁  e₂ следует f(e₁)  f(e₂) и каждый эЭ является образом некоторого eE, то между E и Э существует взаимно однозначное соответствие. В случае, когда Э есть множество действительных чисел, т.е. чисел, используемых в практических расчетах и измерениях, то функция э = f(e) называется скалярной. Часто E является множеством каких- либо функцией, тогда э называют функционалом.

Два множества имеют одинаковую мощность тогда, когда можно установить взаимно однозначное соответствие между их элементами. Множество E является бесконечным, если оно имеет ту же мощность, что и хотя бы одно из его собственных подмножеств (в противном случае E конечно). Мощность конечного множества определяется числом его элементов.

Бесконечное множество E называют счетным, т.е. допускающим принципиальную возможность пересчитать его элементы, если устанавливается взаимно однозначное соответствие между элементами E и элементами множества натуральных чисел.

Числовое множество E называется упорядоченным, если любые два его элемента e₁, e₂ связаны либо отношением e₁  e₂, либо отношением e₁  e₂ (например, множество всех действительных чисел). В этих условиях ê называется верхней границей множества E, если ê  e для всех eE. Наименьшей из имеющихся ê называется точной верхней границей (супремум) sup E. Аналогично определяют нижнюю и точную нижнюю границу множеств (инфимум) inf E. Когда Ē E неограниченно сверху sup Ē = , снизу inf Ē = - .

Пример: принципиально достижимое и реально достигнутое быстродействие ЭВМ при существующем уровне развития техники (второе оказывается точной границей).