8.2. Метод Франка-Вульфа

Пусть требуется найти максимальное значение вогнутой функции

(х₁, х₂, х₃,…, х_n) (8.3)

при условиях

(8.4)

x_j  0, j = 1: n. (8.5)

Характерной особенностью этой задачи является то, что ее система ограничений содержит только линейные неравенства. Эта особенность является основой для замены в окрестности исследуемой точки нелинейной целевой функции линейной, благодаря чему решение исходной задачи сводится к последовательному решению задач линейного программирования.

Процесс нахождения решения задачи начинают с определения точки, принадлежащей области допустимых решений задачи. Пусть это точка х^(k) , тогда в этой точке вычисляют градиент функции (8.3)

(х^(k) ) = (х^(k))/х₁, (х^(k))/х₂, …, (х^(k))/х_n

и строят линейную функцию

F = ((х^(k))/х₁)·x₁ + ((х^(k))/х₂)·x₂ + … + ((х^(k))/х_n)·x_n. (8.6)

Затем находят максимальное значение этой функции при ограничениях (8.4) и (8.5).

Пусть решение данной задачи определяется точкой z^(k). Тогда за новое допустимое решение исходной задачи принимают координаты точки х^(k+1):

х^(k+1) = х^(k) + _k(z^(k) – х^(k) ), (8.7)

где _k – некоторое число, называемое шагом вычислений и заключенное между нулем и единицей (0  _k  1). Это _k берут произвольно или определяют таким образом, чтобы значение функции в точке х^(k+1)(х^(k+1)), зависящее от _k , было максимальным. Для того необходимо найти решение уравнения d/d_k = 0 и выбрать его наименьший корень. Если его значение больше единицы, то следует положить _k = 1. После определения числа _k находят координаты точки х^(k+1), вычисляют значение целевой функции в ней и выясняют необходимость перехода к новой точке х^(k+2). Если такая необходимость имеется, то вычисляют в точке х^(k+1) градиент целевой функции, переходят к соответствующей задаче линейного программирования и находят ее решение. Определяют координаты точки х^(k+2) и исследуют необходимость проведения дальнейших вычислений. После конечного числа шагов получают с необходимой точностью решение исходной задачи.

Итак, процесс нахождения решения задачи (8.3) … (8.5) методом Франка-Вульфа включает следующие этапы:

1. Определяют исходное допустимое решение задачи.

2. Находят градиент функции (8.3) в точке допустимого решения.

3. Строят функцию (8.6) и находят ее максимальное значение при условиях (8.4) и (8.5).

4. Определяют шаг вычислений.

5. По формулам (8.7) находят компоненты нового допустимого решения.

6. Проверяют необходимость перехода к последующему допустимому решению. В случае необходимости переходят к этапу 2, в противном случае найдено приемлемое решение исходной задачи.

Пример 8.1. Методом Франка-Вульфа найти решение задачи, состоящей в определении максимального значения функции

 = 2х₁ + 4х₂ – х₁² – 2х₂² (8.8)

при условиях

(8.9)

х₁, х₂  0. (8.10)

Решение. Найдем градиент функции

 = [/х₁, /х₂] = (2 – 2х₁, 4 – 4х₂)

и в качестве исходного допустимого решения задачи возьмем точку х⁽⁰⁾ = (0, 0), а в качестве критерия оценки качества получаемого решения – неравенство

(х^(k+1) ) - (х^(k) ) < , где  = 0,01.

I и т е р а ц и я. В точке х⁽⁰⁾ градиент (х⁽⁰⁾ ) = (2, 4). Находим максимум функций

F₁ = 2х₁ + 4х₂ (8.11)

при условиях (8.9) и (8.10)

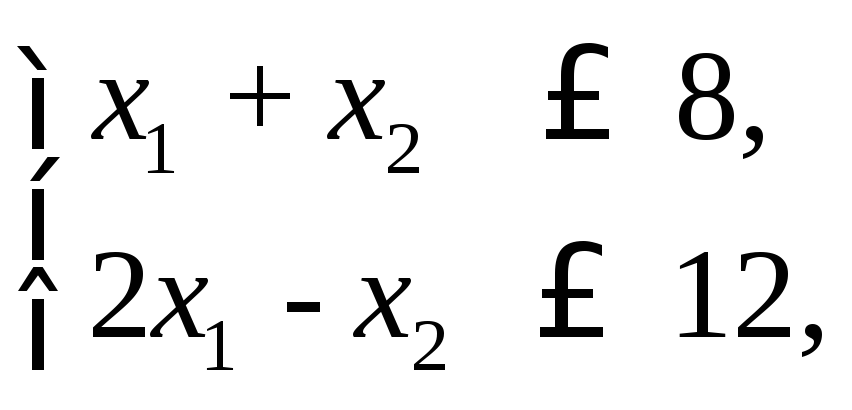(8.12)

х₁, х₂  0. (8.13)

З

х₁ + 2х₂ = 8 х₂

8

2х₁ – х₂ =12

4

-8 -4 0 4 8 12 х₁

-4

-8

-12

адача (8.11) … (8.13) имеет оптимальный план (см. рис. 8.2)z⁽⁰⁾ = (0; 4, т. А).

Рис. 8.2. Оптимальный план z⁽⁰⁾

Найдем новое допустимое значение исходной задачи по формуле (8.7):

х⁽¹⁾ = х⁽⁰⁾ + ₁(z⁽⁰⁾ – х⁽⁰⁾), (8.14)

где 0  ₁  1.

Подставив вместо х⁽⁰⁾ и z⁽⁰⁾ их значения, получим

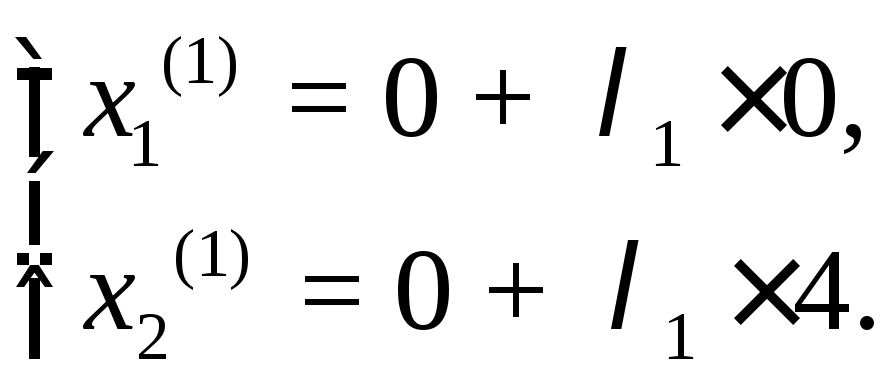(8.15)

Определим теперь число ₁. Подставив в равенство (8.8) вместо х₁ и х₂ их значения в соответствии с соотношениями (8.15) (_) = 16_ - 32_², найдем производную этой функции по _ и приравняем ее нулю (_) = 16 - 64_ = 0. Решая это уравнение, получим _ = 1/4 = 0,25. Поскольку найденное значение _ заключено между 0 и 1, принимаем его за величину шага. Таким образом, х⁽¹⁾ = (0, 1), (х⁽¹⁾) = 2, (х⁽¹⁾) - (х⁽⁰⁾) = 2 >  = 0,01.

II и т е р а ц и я. Градиент целевой функции исходной задачи в точке х⁽¹⁾ есть (х⁽¹⁾) = (2, 0). Находим максимум функции F₂ = 2х₁ при условиях (8.9) и (8.10). Решением является (см. рис. 8.2) z⁽¹⁾ = (6,4; 0,8, т. В). Определяем теперь х⁽²⁾ = х⁽¹⁾ + ₂(z⁽¹⁾ – х⁽¹⁾). Последнее равенство перепишем следующим образом:

(8.16)

Подставляя теперь в функцию (8.8) вместо х₁ и х₂ их значения в соответствии с соотношениями (8.16), получаем

(₂) = 2 + 12,8₂ - 41,04₂²,

откуда (₂) = 12,8 - 41,04₂. Приравнивая (₂) нулю и решая полученное уравнение, находим ₂ 0,16. Таким образом,

т.е. х⁽²⁾ = (1,02; 0,97), (х⁽²⁾) = 2,9978, (х⁽²⁾) - (х⁽¹⁾) = 2,9978 – 2 = 0,9978 >  = 0,01.

III и т е р а ц и я. Градиент функции  в точке х⁽²⁾ есть (х⁽²⁾) = (-0,04; 0,12). Находим максимум функции F₃ = -0,04х₁ + 0,12х₂ при условиях (8.9) и (8.10). Решением является (см. рис. 8.2) z⁽²⁾ = (0; 4, т. А).

Определяем х⁽³⁾ = х⁽²⁾ + ₃(z⁽²⁾ – х⁽²⁾). Имеем

(₃) = 2,9978 + 0,4044₃ – 19,4022₃²,

(₃) = 0,4044 – 38,8044₃.

Решая уравнение (₃) = 0, находим ₃  0,010. Следовательно,

х⁽³⁾ = (1,0098; 1,0003), (х⁽³⁾) = 2,99991,

(х⁽³⁾) - (х⁽²⁾) = 2,99991 – 2,9978 = 0,00211 <  = 0,01.

Таким образом, х⁽³⁾ = (1,0098; 1,0003) является искомым решением исходной задачи. Задав меньшую величину , можно было бы, совершив дополнительные приближения, еще ближе подойти к точке максимального значения целевой функции.

Пример 8.2. Определить градиентным методом максимум функции

 = 4х₁ + 2х₂ – х₁² – х₂² + 5,

начав итерационный процесс с точки х⁽⁰⁾ = (4, 5).