7. Главный минор и ранг матрицы

Если А – матрица порядка nn, то ее главный минор (M(i, j)) порядка k есть подматрица порядка kk, полученная путем исключения из матрицы А произвольных n-k строк (i) и соответствующих этим строкам столбцов (j), т. е. строк и столбцов с одинаковыми номерами. Например,

.

Главными минорами порядка 1 являются диагональные элементы 1, 5 и 9. Главные миноры порядка 2 представляют собой следующие матрицы порядка (2∙2):

.

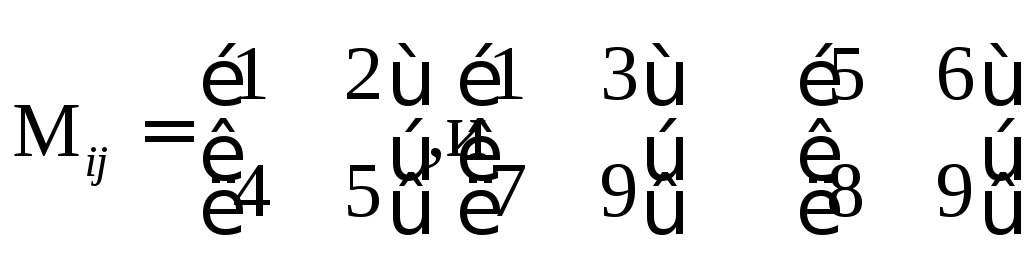Главным минором порядка 3 является сама матрица А. Если удаляются строки и столбцы с некоторого до n, то главный минор называется угловым. Например, − сам определитель.

Определитель главного минора называется главным определителем. Общее количество главных определителей для квадратной матрицы порядка nхn равно 2ⁿ-1.

Ведущий главный минор порядка k матрицы порядка nn строится путем исключения последних n-k строк и соответствующих этим строкам столбцов. В примере ведущий главный минор порядка 1 равен 1 (следует исключить последние две строки и два столбца). Ведущий главный минор порядка 2 есть матрица , а ведущий главный минор порядка 3 – сама матрицаА. Количество ведущих главных определителей матрицы порядка nn равно n.

Выделим в определителе (1.6) некоторый элемент a_ij. Соберем в сумме все члены определителя, в которые в качестве множителя входит выделенный нами элемент a_ij и вынесем его за скобки. Оставшееся в скобках выражение обозначается через A_ij и называется алгебраическим дополнением элемента a_ij в определителе D.

Пусть роль элемента а_ij играет, например, элемент а₂₃. Его алгебраическим дополнением является выражение А₂₃ = а₁₂а₃₁-а₁₁а₃₂.

Таким же путем можно найти алгебраические дополнения остальных элементов определителя:

D = а₁₃А₁₃+а₂₃А₂₃+а₃₃А₃₃

В общем виде алгебраическое дополнение элемента с индексом (i, j) будет иметь вид

А_ij = (-1)^i+jM_ij, i, j = 1, 2, . . . , n (1.7)

С учетом (1.7) можно сказать, что определитель матрицы является разложением по алгебраическим дополнениям

, j = 1, 2, . . . , n (разложение по столбцу)

, i = 1, 2, . . . , n (разложение по строке)

Если А – матрица порядка nхn, то

,

где М_i1 представляет собой подматрицу матрицы А, полученную путем исключения строки i и столбца 1. Например, если

, то

Определитель равен сумме произведений всех элементов любого из его столбцов на их алгебраические дополнения. Порядок наибольшего отличного от нуля минора данной матрицы называется рангом R(A).

R(A) ≤ min(m, n).

Рангом квадратной матрицы А называют наибольший порядок не обращающегося в ноль минора этой матрицы.

Матрица называется невырожденной (неособенной или несингулярной), если R(A) = n , т. е. Det(A) ≠ 0. Матрица называется вырожденной, если Det(A) = 0.

8. Линейные комбинации

Рассмотрим два n – мерных вектора а = (а₁, а₂, . . . , а_n)^Т и b = (b₁, b₂, . . . , b_n)^T. Вектор а называется пропорциональным вектору b , если существует число k, такое что a = kb, т. е. если компоненты вектора а пропорциональны компонентам вектора b.

Согласно определению, нуль-вектор пропорционален любому вектору, так как справедливо равенство 0_n = 0_n∙a.

Понятие пропорциональности двух векторов является частным случаем более общего понятия – линейной комбинации.

Имея набор, состоящий из n векторов (а₁, а₂, . . . , а_n)^Т, и набор из n чисел (k₁, k₂, . . . , k_n) можно составить линейную комбинацию векторов (а_i) с коэффициентами (k_i). Для этого надо i-й вектор умножить на i-й скаляр и все полученные таким образом произведения сложить, т. е. линейной комбинации векторов (а_i) с коэффициентами (k_i) называется вектор b, определенный равенством

b = k₁a₁+k₂a₂+ . . . +k_na_n.

Эта процедура есть не что иное, как умножение матрицы А со столбцами (а_i) на вектор с компонентами (k_i), т. е. b = (а₁, а₂, . . . , а_n) (k₁, k₂, . . . , k_n)^T.

Таким образом, любое произведение матрицы и вектора есть линейная комбинация столбцов матрицы с коэффициентами, равными компонентам вектора.

Линейную комбинацию с нулевыми коэффициентами принято называть тривиальной, а если хотя бы один из коэффициентов в линейной комбинации отличен от нуля, ее называют нетривиальной.

Например, вектор b = (12; 46) является линейной комбинацией векторов

а₁ = (12; 12) и а₂ = (0; 34): b = а₁+а₂.

Частным случаем линейной комбинации является неотрицательная комбинация (k_i 0), в которой выполняется условиеk₁+k₂+ . . . +k_n = 1 . Тогда линейная комбинация называется выпуклой комбинацией.