6.1.2. Метод исключения переменных Пусть дана задача линейного программирования в канонической форме

f(x) = ,

а_ij x_j = b_{i ,} i  :m, (6.8)

x_j ≥ 0, j = 1:n,

где число переменных на два больше числа ограничений − равенств, т.е. n -m= 2, причем ранг матрицыА =m. Тогда две переменные в указанной системе уравнений, скажемх₁их₂, являются свободными, т.е. через них можно выразить все остальные переменные:

, (6.9)

где − некоторые числа. Подставляя эти выражения в целевую функцию, получаем

f=γ₁х₁+γ₂х₂+δ, (6.10)

где γ₁, γ₂, δ − некоторые числа.

Рассмотрим задачу линейного программирования с двумя переменными:

f=γ₁х₁+γ₂х₂ →max,

Используя геометрические построения, находим ее решение (). Подставляя эти числа в (6.9), (6.10), получаем решение и значение исходной задачи (6.8).

Пример6.2.Используя графический метод, найти решение

хх₁ х₂ min,

х₁+х₂ ,

2х₁+х₂ 8,

х₂ 3,

х₁, х₂  0.

Рис. 6.2. Допустимое множество задачи 6.2

Решение. Изобразим на плоскости (х₁, х₂) допустимое множество  данной задачи (многоугольник ABCDE, рис. 6.2) и одну из линий уровня -х₁ -2х₂ = - 3 целевой функции х. Направление убывания (x) указывает вектор l = (1,2). Совершая параллельный перенос линии уровня вдоль направления l, находим ее крайнее положение. В этом положении прямая -х₁ - 2х₂ = - 3 проходит через сторону CD полиэдра ABCDE. Таким образом, все точки отрезка CD являются точками минимума функции х на множестве X. Так как концы C и D этого отрезка имеют координаты (1,3) и (3,2) соответственно, то любая точка минимума функции х представима в виде

где . Минимальное значение целевой функции^*=(х*) = –7.

Пример 6.3.Решить графическим методом задачу линейного программирования:

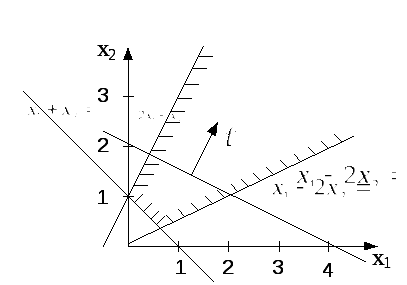
Рис. 6.3. Неограниченное многоугольное множество

Решение. Допустимое множество этой задачи представляет собой неограниченное многоугольное множество (рис. 6.3). Функцияf(x) убывает в направленииl= (1,2). При параллельном переносе линии уровнявдоль направленияlона всегда пересекает множествоХ, а целевая функцияf(x) неограниченно убывает. Поэтому рассмотренная задача не имеет решений.

Пример 6.4.Найти максимальное значение функции

f(x) =-16x₁ - x₂+x₃ + 5x₄+ 5x₅

при условиях:

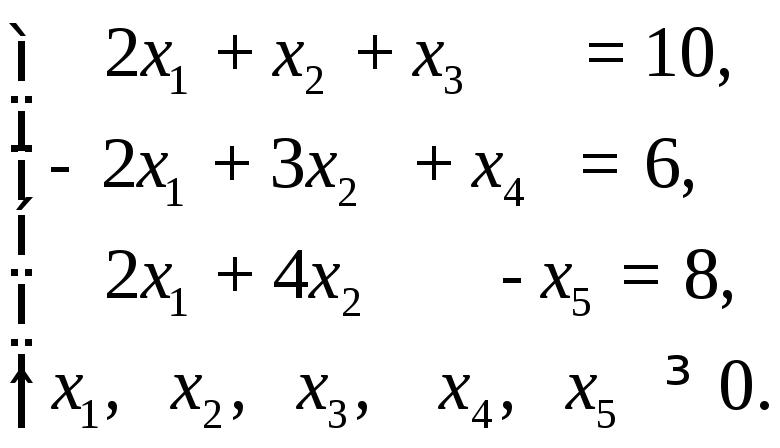
Решение.В отличие от рассмотренных выше задач в исходной задаче ограничения заданы в виде уравнений. При этом число неизвестных равно пяти. Поэтому данную задачу следует свести к задаче, в которой число неизвестных было бы равно двум. В рассматриваемом случае это можно сделать путем перехода от исходной задачи, записанной в форме основной, к задаче, записанной в форме стандартной.

Из целевой функции исходной задачи исключаем переменные x₃, x₄, x₅ с помощью подстановки их значений из соответствующих уравнений системы ограничений. Получаем постановку задачи в стандартной форме:

f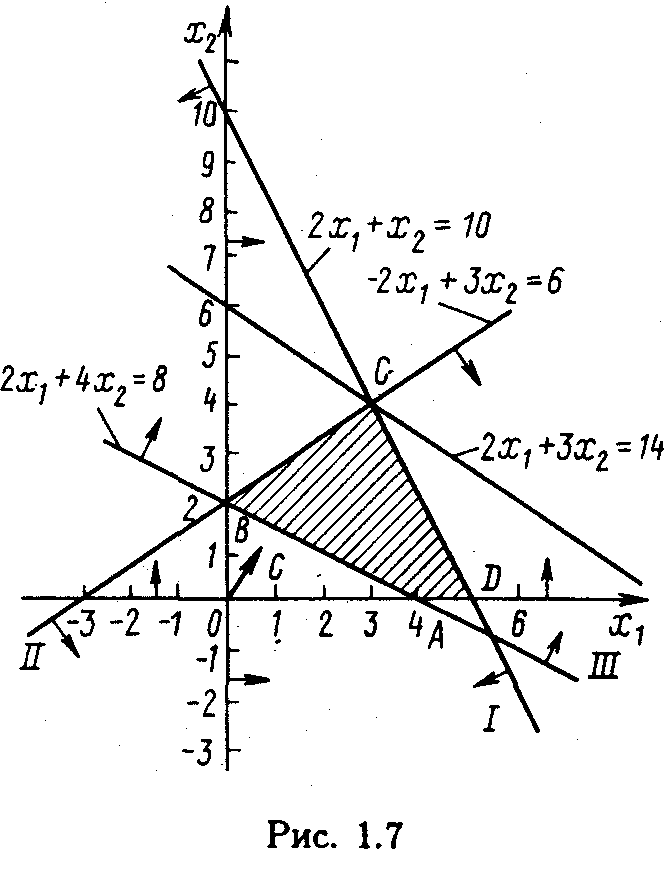(x) = 2x₁ +3x₂,

при условиях:

Рис. 6.4. Многоугольник решений

Построим многоугольник решений полученной задачи (рис. 6.4). Как видно из рис. 6.4., максимальное значение целевая функция задачи принимает в точке С пересечения прямыхIиII.Вдоль каждой из граничных прямых значение одной из переменных, исключенной при переходе к соответствующему неравенству, равно нулю. Поэтому в каждой из вершин полученного многоугольника решений последней задачи по крайней мере две переменные исходной задачи принимают нулевые значения. Так, в точкеС имеемx₃ = 0 иx₄ = 0. Подставляя эти значения в первое и второе уравнения системы ограничений исходной задачи, получаем систему двух уравнений

решая которую, находим x₁* =3,x₂* = 4.

Подставляя найденные значения x₁иx₂в третье уравнение системы ограничений исходной задачи, определяем значение переменнойx₅ равное 14.

Следовательно, оптимальным планом рассматриваемой задачи является x* = (3; 4; 0; 0; 14). При этом плане значение целевой функции есть _max = 18.