4.4. Теорема Вейерштрасса

Сформулированная выше задача оптимизации (4.1) имеет решение при любых целевых функциях и допустимых множествах. Существуют задачи, в которых невозможно найти оптимальную точку и оптимальное значение. Например, не существует точек минимума у функции одной переменной  на множестве Х в случаях изображённых на рис.4.7.

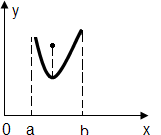
Х=[a,b) Х=[a,+) Х=[a,b]

Рис. 4.7. Графики функций, не имеющие минимума

В первом случае точка минимума не существует, поскольку множество Х не замкнутое. Во втором случае – вследствие неограниченности Х. В третьем случае минимум не достигается из-за того, что функция f не является непрерывной.

Итак, при изучении задач оптимизации в первую очередь возникает вопрос о существовании решения. В этом случае имеет место, следующее утверждение, которое называют теоремой Вейерштрасса.

Теорема 4.5. Пусть Х – компакт в (замкнутое ограниченное множество), f – непрерывная функция на Х. Тогда точка глобального минимума функции f на Х (глобальное решение задачи (4.1)) существует.

В дальнейшем окажется полезной и несколько иная форма данной теоремы.

Теорема 4.6. Пусть Х – замкнутое множество в ,  – непрерывная функция на Х, причём существует такая точка х’Х, что множество вида N(x’)={xХ| (x)(x’)} ограничено. Тогда точка глобального минимума функции  на Х существует (рис. 4.8)

Следствие:

Если функция  (х) непрерывна на и , то (x) достигает своего абсолютного минимума (наименьшего значения) на любом замкнутом подмножестве .

Рис. 4.8. График функции, имеющий глобальный минимум

Пример 4.7.

f(x) = x₁⁴+x₂⁴-x₁²-2x₁x₂-x₂² →extr.

Решение. Запишем необходимое условие экстремума I порядка:

Решая эту систему уравнений, находим стационарные точки x¹=(x₁,x₂) = (1,1), х² = (-1,-1), х³ = (0,0). Для проверки условий второго порядка выписываем матрицу вторых производных:

==

,.

Матрица по критерию Сильвестра положительно определена. По достаточному условию локального экстремума функции нескольких переменных точки (1,1) и (-1,-1) доставляют локальный минимум функцииf.

Поскольку f(x)= =+, то по следствию из теоремы Вейерштрасса она достигает своего абсолютного минимума. Следовательно, (1,1), (-1,-1)absmin, S_min = f(1,1) = f(-1,-1) = -2.

Матрица по критерию Сильвестра не является ни положительно, ни отрицательно определенной. Она является неположительно определенной матрицей (А ≤ 0) и не является неотрицательно определенной матрицей (A < 0). Следовательно, не выполняется необходимое условие локального минимума. Поэтому х³ = (0,0) locmin f. Поскольку

f(h,-h) = 2h⁴ > 0 = f (x³)

при малых h ≠0, то х³ locmax f. Очевидно, что f_max = + .

4.5. Обобщенная задача оптимизации

В теории оптимизации иногда более удобно рассматривать общую задачу оптимизации, в которой понятие решение определяется таким образом, что оно всегда существует. Для того чтобы сформулировать эту обобщённую задачу, понадобится определение точной нижней грани.

Число (или символ – ) называют точной нижней гранью или инфимумом функции  на множестве X, если неравенство   (x) имеет место для всех хХ и, кроме того, для любого числа ’> найдётся точка х’Х такая, что верно неравенство (x’)<’. Тот факт, что– точная нижняя грань функциина множествеХ, записывают в виде

(4.8)

Аналогично вводится понятие точной верхней грани. Число (или символ +) называют точной верхней гранью или супремумом функции  на множестве Х, если неравенство f ⁰⁰ (x) справедливо для всех хХ и для любого числа ’ < f ⁰⁰ найдётся точка х’Х такая, что верно неравенство (x’) >’. Для точной верхней грани используется обозначение

Как указано выше, не всегда можно указать точку, в которой точная грань достигается, т.е. точку , для которой . Поэтому в обобщённой задаче минимизации под решением понимают не отдельную точку, как это имеет место в обычной задаче оптимизации, а последовательность точек , , k =1,2,…,такую, что

(4.9)

Эта последовательность всегда существует и называется, минимизирующей последовательностью.

Таким образом, обобщённая задача минимизации целевой функции  на множестве Х заключается в отыскании числа (или символа -)и последовательности точек , , k = 1,2,…, таких, что выполняются равенства (4.8) ... (4.9).