
- •5. Численные методы решения задач одномерной оптимизации
- •Прямые методы
- •Метод перебора
- •Методы исключения интервалов
- •Этап установления границ интервала
- •Этап уменьшения интервала. Метод деления интервала пополам (дихотомии)
- •Метод золотого сечения
- •5.2. Методы, использующие производные функции
- •Условие Липшица
- •5.2.2. Метод Ньютона – Рафсона
- •5.2.3.Метод секущих
Метод золотого сечения
Метод золотого
сечения также являетсяпоследовательным
методом минимизации. Этот метод
использует найденные значения ¦(x)
более рационально, чем метод деления
интервала пополам, что позволяет
переходить к очередному интервалу,
содержащему x![]() после вычисления одного, а не двух
значений ¦(x).
после вычисления одного, а не двух
значений ¦(x).
Метод золотого сечения тесно связан с числами Фибоначчи, которые определяются с помощью рекуррентного соотношения:
F0 = 0, F1 = 1, Fi = Fi-1 + Fi-2, i ≥ 2.
Таким образом, числа Фибоначчи образуют последовательность, в которой каждое очередное число представляет собой сумму двух предыдущих:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…
Рассмотрим на
исходном отрезке [a;
b]
точку x![]() и вычислим ¦(x
и вычислим ¦(x![]() ).
Зная значение целевой функции в одной
точке, невозможно сузить область поиска
точки x*.
Поэтому выберем вторую точку x
).
Зная значение целевой функции в одной
точке, невозможно сузить область поиска
точки x*.
Поэтому выберем вторую точку x![]() так, чтобы a
< x
так, чтобы a
< x![]() <
x
<
x![]() <
b,
и вычислим ¦(x
<
b,
и вычислим ¦(x![]() ).
Возможен один из следующих двух случаев:
¦(x
).
Возможен один из следующих двух случаев:
¦(x![]() )
£
¦(x
)
£
¦(x![]() )
или ¦(x
)
или ¦(x![]() )
³
¦(x
)
³
¦(x![]() ).
).
Согласно свойству
унимодальной функции: если ¦(x![]() )
£
¦(x
)
£
¦(x![]() ),
то x
),
то x![]() < x
< x![]() ;
если же ¦(x
;
если же ¦(x![]() )
³
¦(x
)
³
¦(x![]() ),
то x
),
то x![]() > x
> x![]() ;
в первом случае искомая точка x
;
в первом случае искомая точка x![]() не может быть на отрезке [x
не может быть на отрезке [x![]() ;
b],
а во втором − на отрезке [a;
x
;
b],
а во втором − на отрезке [a;
x![]() ]
(эти отрезки на рис. 5.3. отмечены
штриховкой). Следовательно, теперь
область поиска сужается и следующую
точку x
]
(эти отрезки на рис. 5.3. отмечены
штриховкой). Следовательно, теперь
область поиска сужается и следующую
точку x![]() следует брать в одном из укороченных
отрезков [a;
x
следует брать в одном из укороченных
отрезков [a;
x![]() ]
или [x
]
или [x![]() ;
b].
;
b].

Рис. 5.3. Уменьшение интервала поиска точки минимума методом золотого сечения
Установим, где на
исходном отрезке лучше всего выбрать
точки x![]() и x
и x![]() .
Так как первоначально ничего неизвестно
о положении точки x
.
Так как первоначально ничего неизвестно
о положении точки x![]() ,
то оба указанных выше случая равновозможны,
т.е. “лишним” может оказаться любой из
отрезков [x
,
то оба указанных выше случая равновозможны,
т.е. “лишним” может оказаться любой из
отрезков [x![]() ;
b]
и [a;
x
;
b]
и [a;
x![]() ].
Отсюда ясно, что точки x
].
Отсюда ясно, что точки x![]() и x
и x![]() должны быть расположены симметрично
относительно середины отрезка [a;
b].
Чтобы максимально сузить область поиска,
эти точки должны быть “поближе” к
середине исходного отрезка. Если их
взять рядом с серединой исходного
отрезка, то на втором этапе сужение
области поиска будет незначительным
(рис. 5.4). На втором этапе сужения области
поискапотребуется вычислить лишь одно
значение ¦(x
должны быть расположены симметрично
относительно середины отрезка [a;
b].
Чтобы максимально сузить область поиска,
эти точки должны быть “поближе” к
середине исходного отрезка. Если их
взять рядом с серединой исходного
отрезка, то на втором этапе сужение
области поиска будет незначительным
(рис. 5.4). На втором этапе сужения области
поискапотребуется вычислить лишь одно
значение ¦(x![]() ),
которое будем сравнивать с уже имеющимся
значением ¦(x
),
которое будем сравнивать с уже имеющимся
значением ¦(x![]() )
или ¦(x
)
или ¦(x![]() )
в зависимости от того, какой из двух
случаев реализовался.
)
в зависимости от того, какой из двух
случаев реализовался.

Рис.
5.4. К выбору пробных точек x![]() и x
и x![]()
Поэтому, с одной
стороны, точки x![]() и x
и x![]() следует выбирать рядом с серединой
отрезка, а с другой – слишком близкими
их брать нельзя. Для того чтобы найти
“золотую середину” используется метод
“золотого сечения”.
следует выбирать рядом с серединой
отрезка, а с другой – слишком близкими
их брать нельзя. Для того чтобы найти
“золотую середину” используется метод
“золотого сечения”.
Поиск с помощью метода золотого сечения основан на разбиении отрезка прямой на две части, известном как “золотое сечение” – отношение длины всего отрезка к большей части равно отношению большей части к меньшей.
Рассмотрим
симметричное расположение двух пробных
точек на исходном интервале единичной
длины (рис. 5.5). Пробные точки x
·![]() ,
x
,
x![]() отстоят от
отстоят от 

 расстоянииF.
При таком симметричном расположении
длина остающегося после исключения
интервала всегда равна F
независимо от того, какое из значений
функции в пробных точках оказывается
меньшим.
расстоянииF.
При таком симметричном расположении
длина остающегося после исключения
интервала всегда равна F
независимо от того, какое из значений
функции в пробных точках оказывается
меньшим.
![]()

Рис. 5.5. Поиск пробных точек с помощью метода золотого сечения
Предположим, что
исключается правый подынтервал. На рис.
5.6. показано, что оставшийся подынтервал
длины F
содержит одну пробную точку x![]() ,
расположенную на расстоянии (1 − F)
от левой граничной точки. Чтобы точки
x
,
расположенную на расстоянии (1 − F)
от левой граничной точки. Чтобы точки
x![]() =
1 − F
и x
=
1 − F
и x![]() =
F
де лили отрезки [0; F]
и [0; 1] в одном и том же отношении должно
выполняться равенство
=
F
де лили отрезки [0; F]
и [0; 1] в одном и том же отношении должно
выполняться равенство
![]() =
=
![]() или F
или F![]() =1
− F,
находим положительное значение F
=
=1
− F,
находим положительное значение F
=
![]() »
0,62.
»
0,62.

Рис. 5.6. Интервалы, полученные методом золотого сечения
Таким образом,
x![]() =
1 − F=
=
1 − F=
![]() »
0,38, x
»
0,38, x![]() =
F=
=
F=
![]() .
Дроби F
.
Дроби F![]() =
=
![]() и F
и F![]() =
=
![]() называются дробями
Фибоначчи
или числа Фибоначчи (Bonaccio(итал.),
сын Боначио − добродушный, простодушный,
т.е. сын добряка, сын удачника). Это
название им дал Леонардо Фибоначчи из
Пизы, который первым открыл их еще в
1202 г., подсчитывая, сколько пар потомства
могут дать в год пара кроликов и их
последующее потомство.
называются дробями
Фибоначчи
или числа Фибоначчи (Bonaccio(итал.),
сын Боначио − добродушный, простодушный,
т.е. сын добряка, сын удачника). Это
название им дал Леонардо Фибоначчи из
Пизы, который первым открыл их еще в
1202 г., подсчитывая, сколько пар потомства
могут дать в год пара кроликов и их
последующее потомство.
Для того чтобы
симметрия поискового образа сохранялась,
расстояние (1 - F)
должно составлять F-
ю часть длины интервала (которая равна
F).
При таком выборе F
следующая пробная точка x![]() размещается на расстоянии, равномF-
й части длины интервала, от правой
граничной точки интервала (рис. 5.7.).
Отсюда следует, что при выборе F
в соответствии с условием 1 − F=
F
размещается на расстоянии, равномF-
й части длины интервала, от правой
граничной точки интервала (рис. 5.7.).
Отсюда следует, что при выборе F
в соответствии с условием 1 − F=
F![]() симметрия поискового образца (рис. 5.5)
сохраняется при переходе к уменьшенному
интервалу (рис. 5.7.). Схема поиска, при
которой пробные точки делят интервал
в этом отношении, известна под названиемпоиска с
помощью метода золотого сечения.
симметрия поискового образца (рис. 5.5)
сохраняется при переходе к уменьшенному
интервалу (рис. 5.7.). Схема поиска, при
которой пробные точки делят интервал
в этом отношении, известна под названиемпоиска с
помощью метода золотого сечения.

Рис. 5.7. Симметрия золотого сечения интервала
Для произвольного отрезка [a; b] выражения для пробных точек примут вид
x![]() =a
+ F
=a
+ F![]() (b
− a),
x
(b
− a),
x![]() =a
+ F
=a
+ F![]() (b
− a)
(5.3)
(b
− a)
(5.3)
Зная одну из точек золотого сечения отрезка [a; b], другую можно найти по одной из формул
x![]() =
a+
b
− x
=
a+
b
− x![]() ,
x
,
x![]() = a+
b
− x
= a+
b
− x![]() (5.4)
(5.4)
Пусть ¦(x)Î
Q[a;
b]
и требуется найти точку минимума x![]() функции ¦(x)
на [a;
b].
Построим последовательности {a
функции ¦(x)
на [a;
b].
Построим последовательности {a![]() },
{b
},
{b![]() }
и {
}
и {![]()
![]() },
n
= 1,2,…, следующим образом:
},
n
= 1,2,…, следующим образом:
a![]() =a
=a![]() ,b
,b![]() =x
=x![]() ,
,
![]()
![]() =x
=x![]() ,если
¦(x
,если
¦(x![]() )£
¦(x
)£
¦(x![]() );
(5.5)
);
(5.5)
a![]() = x
= x![]() ,
b
,
b![]() = b
= b![]() ,
,
![]()
![]() = x
= x![]() ,
если ¦(x
,
если ¦(x![]() )
>
¦(x
)
>
¦(x![]() ),
n
= 2,3,…,
),
n
= 2,3,…,
где
a![]() = a,
b
= a,
b![]() = b,
x
= b,
x![]() и x
и x![]() − первая и вторая точки золотого сечения
(5.3) отрезка [a
− первая и вторая точки золотого сечения
(5.3) отрезка [a![]() ;
b
;
b![]() ].
].
Для определения
чисел a![]() ,
b
,
b![]() ,
,
![]()
![]() ,
по найденным a
,
по найденным a![]() ,
b
,
b![]() ,
,
![]() необходимо выполнить следующие операции:
необходимо выполнить следующие операции:
найти одну из точек золотого сечения отрезка [a
 ;
b
;
b ]
по известной другой точке
]
по известной другой точке
 ,
используя формулы (5.4). При определенииx
,
используя формулы (5.4). При определенииx с большой точностью, чтобы избежать
накопления ошибок округления, обычно
точки золотого сечения отрезка [a
с большой точностью, чтобы избежать
накопления ошибок округления, обычно
точки золотого сечения отрезка [a ;
b
;
b ]
находят по формулам (5.3) и в качестве
x
]
находят по формулам (5.3) и в качестве
x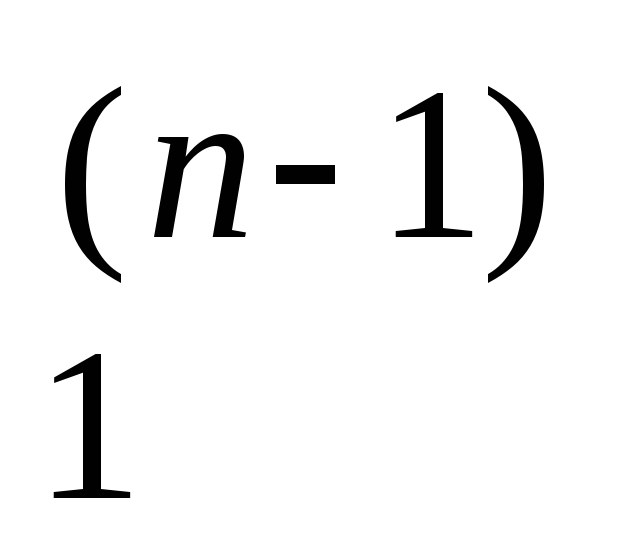 и x
и x используют
используют
 и ту из найденных точек, которая больше
отличается от
и ту из найденных точек, которая больше
отличается от ;
;вычислить значение ¦(x) во вновь найденной точке золотого сечения (значение в другой точке
 уже вычислено на одном из предыдущих
шагов);
уже вычислено на одном из предыдущих
шагов);сравнить значения ¦(x
 )
и ¦(x
)
и ¦(x )
и найти a
)
и найти a ,
b
,
b и
и
 по формулам (5.5).
по формулам (5.5).
Таким образом, на
каждом шаге определения a![]() ,
b
,
b![]() и
и
![]() n
= 2,3,…, требуется вычисление одного
значения ¦(x).
Положив x
n
= 2,3,…, требуется вычисление одного
значения ¦(x).
Положив x![]() »
»
![]() найдем точку минимумаx
найдем точку минимумаx![]() с точностьюe
с точностьюe![]() :
:
½x![]() -
-
![]() ½
£
e
½
£
e![]() = [(
= [(![]() -
1)/2]n∙(b
− a),
-
1)/2]n∙(b
− a),
отсюда
следует, что число шагов n
метода золотого сечения, обеспечивающее
заданную точность e
нахождения точки x![]() ,
должно удовлетворять неравенству
,
должно удовлетворять неравенству
n
³
ln(![]() )
/ln(
)
/ln(![]() )
»
− 2,1 ln(
)
»
− 2,1 ln(![]() )
(5.6)
)
(5.6)
Пример 5.4. Решить пример 5.2. методом золотого сечения.
Вычисления проведем по формулам (5.5), представив результаты в таблице 5.3, где стрелками отмечены сохраняющиеся при переходе к следующему шагу значения.
Таблица 5.3
Значения пробных точек и функции ¦(x)
|
N |
e |
a |
B |
x |
x |
¦(x |
¦(x |
Примечание |
|
|
0,309 |
1,5 |
2,0 |
1,691 |
1,809 |
-92,049 |
-91,814 |
¦(x |
|
|
0,191 |
1,5 |
1,809 |
1,618 |
1,691 |
-91,464 |
-92,049 |
¦(x |
|
|
0,118 |
1,618 |
1,809 |
1,691 |
1,736 |
-92,049 |
-92,138 |
¦(x |
|
|
0,073 |
1,691 |
1,809 |
1,736 |
1,764 |
-92,138 |
-92,083 |
¦(x |
|
5 |
0,045 |
|
|
|
1,736 |
|
-92,138 |
e
|
Из таблицы 5.3
получаем x![]() »
»
![]() = 1,736, ¦
= 1,736, ¦![]() »
¦(
»
¦(![]() )=
− 92,138. Если воспользоваться формулой
(5.6), то n
можно определить заранее. В нашем случае
n
³
4,79, т.е. n
= 5.
)=
− 92,138. Если воспользоваться формулой
(5.6), то n
можно определить заранее. В нашем случае
n
³
4,79, т.е. n
= 5.


 1
1
 2
2
 3
3
 4
4