Расчет дисперсии по формуле по индивидуальным данным и в рядах распределения.

Техника вычисления дисперсии сложна, а при больших значениях вариант и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.

Свойства дисперсии.

1. Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.

2. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.

3. Уменьшение или увеличение каждого значения признака в какое-то число раз к соответственно уменьшает или увеличивает дисперсию в раз, а среднее квадратическое отклонение - в к раз.

4. Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной: . Если А равна нулю, то приходим к следующему равенству:, т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.

Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.

Порядок расчета дисперсии простой:

1) определяют среднюю арифметическую ;

2) возводят в квадрат среднюю арифметическую;

3) возводят в квадрат каждую варианту ряда ;

4) находим сумму квадратов вариант ;

5) делят сумму квадратов вариант на их число, т.е. определяют средний квадрат ;

6) определяют разность между средним квадратом признака и квадратом средней .

Пример 5.

Имеются следующие данные о производительности труда рабочих:

Таблица 6.4

Табельный номер рабочего	Произведено продукции, шт.
1	8	64
2	9	81
3	10	100
4	11	121
5	12	144
ИТОГО	50	510

Произведем следующие расчеты:

шт.

Пример 6.

Определить дисперсию в дискретном ряду распределения, используя табл. 6.5.

Таблица 6.5.

Произведено продукции 1 рабочим, шт. (х)	Число рабочих, n
8	7	56	64	448
9	10	90	81	810
10	15	150	100	1500
11	12	132	121	1452
12	6	72	144	864
ИТОГО	50	500	510	5074

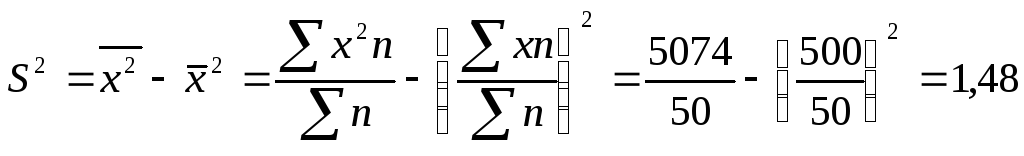
Получим тот же результат, что в табл. 6.3.

Рассмотрим расчет дисперсии в интервальном ряду распределения.

Порядок расчета дисперсии взвешенной (по формуле ):

1. определяют среднюю арифметическую ;

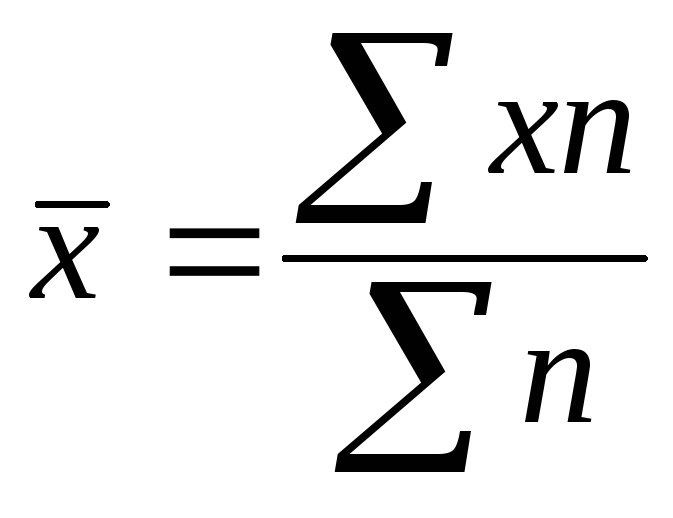2. возводят в квадрат полученную среднюю ;

3. возводят в квадрат каждую варианту ряда ;

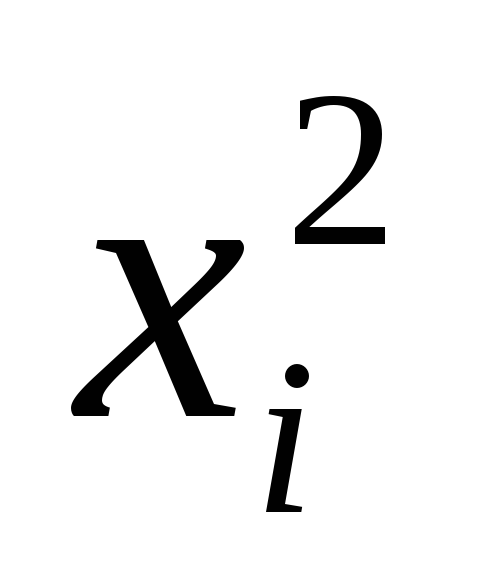4. умножают квадраты вариант на частоты ;

5. суммируют полученные произведения ;

6. делят полученную сумму на сумму весов и получают средний квадрат признака ;

7. определяют разность между средним значением квадратов и квадратом средней арифметической, т.е. дисперсию .

Пример 7.

Имеются следующие данные о распределении посевной площади колхоза по урожайности пшеницы:

Таблица 6.6

Урожайность пшеницы, ц/га	Посевная площадь, га
14 - 16	100	15	1500	225	22500
16 - 18	300	17	5100	289	36700
18 - 20	400	19	7600	361	144400
20 - 22	200	21	4200	441	88200
ИТОГО	1000		18400		341200

В подобных примерах прежде всего определяется дискретное значение признака в каждом интервале, а затем применяется метод расчета, указанный выше:

Средняя величина отражает тенденцию развития, т.е. действие главных причин. Среднее квадратическое отклонение измеряет силу воздействия прочих факторов.