Вариант 27

1. Пользуясь только определениями операций над множествами, докажите тождества: , (AB)(CD)=(AC)(BD).

2. A={a, b, c}, B={1, 2, 3, 4}, P={(a, 1), (a, 2), (a, 4), (c, 3), (c, 2), (c, 4)}, Q={(2, 1), (3, 1), (3, 2), (4, 1), (4, 3)}. Изобразите P, Q графически. Найдите [(PQ)^1] и по матрице отношения найти (PQ)^1. Проверьте с помощью матрицы [Q], является ли отношение Q рефлексивным, симметричным, антисимметричным, транзитивным?

3. Найдите область определения, область значений отношения РZ², (x, y)P  x+y кратно 5. Является ли отношение Р рефлексивным, симметричным, антисимметричным, транзитивным?

Вариант 28

1. Пользуясь только определениями операций над множествами, докажите тождества: , (AB)(CD)=(AC)(BD).

2. A={a, b, c}, B={1, 2, 3, 4}, P={(a, 1), (b, 3), (c, 1), (c, 4), (c, 3), (c, 2)}, Q={(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (2, 3), (3, 3), (3, 2)}. Изобразите P, Q графически. Найдите [(PQ)^1] и по матрице отношения найти (PQ)^1. Проверьте с помощью матрицы [Q], является ли отношение Q рефлексивным, симметричным, антисимметричным, транзитивным?

3. Найдите область определения, область значений отношения РR², (x, y)P  x²+y²=9. Является ли отношение Р рефлексивным, симметричным, антисимметричным, транзитивным?

Вариант 29

1. Пользуясь только определениями операций над множествами, докажите тождества: AB=(B)A, (AB)(CD)=(AC)(BD).

2. A={a, b, c}, B={1, 2, 3, 4}, P={(a, 3),(a, 2), (b, 2), (b, 3), (c, 1), (c, 4)}, Q={(1, 1), (1, 2), (2, 2), (3, 3), (4, 1), (4, 4)}. Изобразите P, Q графически. Найдите [(PQ)^1] и по матрице отношения найти (PQ)^1. Проверьте с помощью матрицы [Q], является ли отношение Q рефлексивным, симметричным, антисимметричным, транзитивным?

3. Найдите область определения, область значений отношения РZ², (x, y)P  5x=6y. Является ли отношение Р рефлексивным, симметричным, антисимметричным, транзитивным?

Вариант 30

1. Пользуясь только определениями операций над множествами, докажите тождества: A\B=A(AB), (AB)C=(AC)(BC).

2. A={a, b, c}, B={1, 2, 3, 4}, P={(a, 1), (a, 2), (a, 4), (b, 1), (b, 4), (c, 3)}, Q={(1, 1), (2, 4), (2, 1), (3, 3), (4, 2), (4, 1)}. Изобразите P, Q графически. Найдите [(PQ)^1] и по матрице отношения найти (PQ)^1. Проверьте с помощью матрицы [Q], является ли отношение Q рефлексивным, симметричным, антисимметричным, транзитивным?

3. Найдите область определения, область значений отношения РR², (x, y)P  x²y. Является ли отношение Р рефлексивным, симметричным, антисимметричным, транзитивным?

Образец решения индивидуального задания

1. Пользуясь только определениями операций над множествами, докажите тождества: A(BC)=(AB)C, (A\B)C=(AC)\(BC).

Решение. 1. Для того, чтобы доказать, пользуясь только определениями операций над множествами, равенство Х=Y двух множеств Х и Y, достаточно показать, что одновременно выполняются включения XY и YX. А для этого достаточно показать, что из xX следует xY, и из xY следует xX.

Докажем, что A(BC)=(AB)C.

Как мы отметили, достаточно показать, что из xA(BC) следует x(AB)C, и из x(AB)C следует xA(BC).

Пусть x(AB)C. Тогда x((AB)\C)(C\(AB)). Значит, или x(AB)\C или xC\(AB), причём х не может лежать одновременно в обоих множествах, так как элемент может лежать только в одном из множеств, участвующих в разности.

Случай 1. x(AB)\C. Тогда xAB, но xC. Отсюда x(A\B)(B\A), xC. Следовательно, xA\B и xC или xB\A и xC. Поэтому xA, xB и xC или xB, xA и xC.

Если xA, xB и xC, то xA, x(B\C)(C\B)=BC, то есть хA\(BC), и тогда х(A\(BC))((BC)\A)=A(BC).

Если xB, xA и xC, то xA и xB\C, и тогда xA и x(B\C)(C\B)=BC, то есть х(BC)\A, и хA(BC).

Случай 2. xC\(AB). Тогда xC, но xAB=(A\B)(B\A). Следовательно, xC, xA\B и xB\A, откуда xC, xA или xB, и xВ или xA. Значит, xC и или xA и xВ, или xA и xВ.

Если xC и xA и xВ, то xA и xC\A, и тогда xA и x(С\B)(B\С). Значит, x(BС)\A, откуда x(A\(BС))((BС)\A)= A(BС).

Если xC и xA и xВ, то xA, xB\С и xС\В, и тогда xA и x(B\С)(С\В)=BС. Следовательно, xА\(ВС)А(ВС).

Таким образом (AB)CA(BC).

Пусть теперь xA(BC). Тогда x(A\(BC))((ВС)\А). Значит, либо xA\(BC), либо x(ВС)\А.

Случай 1. xA\(BC). Тогда xА, и xВС=(В\С)(С\В). Значит, xA и либо xВ\С, либо xС\В. xC. Тогда xA и либо xВ или xС, либо xС или xВ. Это значит, xA и либо xВ и xС, либо xВ и xС, то есть либо xA, xВ и xС, либо xA, xВ и xС.

Если xA, xB и xC, то xA\В и хС. Следовательно, x(А\В)(В\А)=АВ, и xC, то есть х(AB)\C, и тогда х(АВ)\С ((АВ)\С)(С\(АВ))=(AB)C.

Если же xА, xВ и xC, то xA\В или xB\А, и при этом xС. Это означает, что x(А\В)(В\А)=АВ и xС. Значит, хС\(АВ)(AB)C.

Случай 2. x(ВС)\А. Тогда xВС, но xА. Отсюда x(В\С)(С\В), xА. Следовательно, xВ\С и xА или xС\В и xА. Поэтому xВ, xС и xА или xС, xВ и xА.

Если xВ, xС и xА, то xС, x(В\А)(А\B)(B\А)=АВ, то есть х(АВ)\С((АВ)\С)(С\(АВ))=, и хA(BC). хA\(BC), и тогда х(A\(BC))((BC)\A)=(AB)C.

Если xС, xB и xА, то xС\В и хА. Следовательно, x(В\С)(С\В)=ВС, и xА, то есть х(ВС)\А, и тогда х(ВС)\А (А\(ВС))((ВС)\А)=(AB)C.

Таким образом, A(BC)(AB)C.

Так как (AB)CA(BC) и A(BC)(AB)C, то окончательно имеем A(BC)=(AB)C, что и требовалось доказать.

Докажем, что (A\B)C=(AC)\(BC).

Как и выше, нам достаточно показать, что из x(A\B)C следует x(AC)\(BC), и из x(AC)\(BC) следует x(A\B)C.

Пусть х(А\В)С. Тогда х=(a, b), где aА\В и bC. Значит, aА, aB и bC. Тогда х=(a, b)АC и х=(a, b)BC. Следовательно, х(АC)\(BС) и (А\В)С(АC)\(BС).

Обратно, пусть х(АC)\(BС). Тогда хАC и хBC. Значит, х=(a, b), где aА и bC. Так как х=(a, b)BC, то aB. Таким образом, aА, aB и bC. Это означает, что где aА\В и bC. Следовательно, х=(a, b)(А\В)С и (АC)\(BС)(А\В)С.

Окончательно имеем (А\В)С=(АC)\(BС), что и требовалось доказать.

2. A={a, b, c}, B={1, 2, 3, 4}, P={(a, 1), (a, 2), (a, 3), (a, 4), (b, 3), (c, 2)}, Q={(1, 1), (1, 4), (2, 2), (2, 3), (3, 3), (3, 2), (4, 1), (4, 4)}. Изобразите P, Q графически. Найдите [(QP)^1] и по матрице отношения найти (PQ)^1. Проверьте с помощью матрицы [Q], является ли отношение Q рефлексивным, симметричным, антисимметричным, транзитивным?

Решение. Первый способ (декартовый) графического изображения заключается в том, что на двух взаимно перпендикулярных осях отмечаются элементы А и B: на горизонтальной  оси Ох,  элементы А, на вертикальной  оси Оy,  элементы B. Отметив точки с координатами (a, k) такими, что (a, k)Р, получим графическое декартово изображение отношения Р:

Второй способ основан на диаграммах Эйлера-Венна, и заключается в том, что если (a, b)Q, то из a к b проводится стрелка.

По свойствам композиций отношений имеем (PQ)=QP. Далее, по свойствам матриц отношений имеем

[(PQ)]=[QP]=[Q][P]=[Q]^T[P]^T.

Найдём [Q]^T и [P]^T. Матрицы [P]^T и [Q]^T  транспонированные к [P] и [Q]. Поэтому достаточно построить [P], [Q] и протранспонировать их. Матрица [P]  это матрица размерности 34 с элементами (p_ij)_mn= Например, p₁₁=1, так как (a, 1)P, но p₂₁=0, так как (b, 1)P. Таким образом,

[P]= и [P]^T=.

Аналогично, для Q, например, q₁₁= q₂₂= q₃₃= q₄₄=1, так как (1, 1), (2, 2), (3, 3), (4, 4)Q, но q₂₄0, так как (2, 4)Q. В результате имеем

[Q]=и [Q]^T=,

[(PQ)]=[Q]^T[P]^T=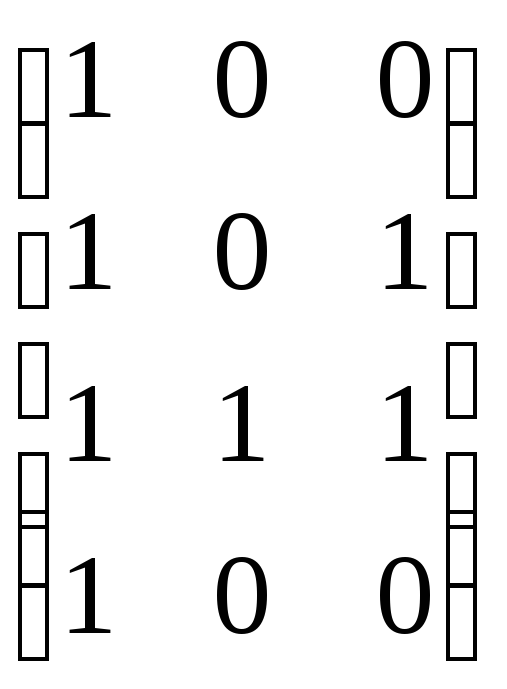=, то есть [(PQ)]=.

Диагональные элементы матрицы [Q] равны 1. Значит, отношение Q рефлексивно. Матрица [Q] несимметрична. Значит, отношение Q не симметрично. Имеем

[QQ]=[Q][Q]===[Q].

В частности, [QQ][Q] и отношение Q транзитивно. Наконец,

[Q][Q]^T==,

то есть вне главной диагонали матрицы [Q][Q]^T есть ненулевые элементы. Значит, Q не является антисимметричной.

Ответ: [(PQ)]=. ОтношениеQ рефлексивно, несимметрично, транзитивно, не антисимметрично.

3. Найдите область определения, область значений отношения РR², (x, y)P  x²+y²=1. Является ли отношение Р рефлексивным, симметричным, антисимметричным, транзитивным?

Решение. Область определения бинарного отношения Р  это множество _Р=х(х, y)Р для некоторого у. Другими словами, _Р  это множество всех значений, которые может принимать х в равенстве x²+y²=1. Значит, _Р=х 1х1 =[1, 1].

Область значений бинарного отношения Р  это множество _Р=у(х, y)Р для некоторого х. То есть, это  множество всех чисел, которые может принимать у. Значит, _Р=у 1у1 =[1, 1].

Отношение Р рефлексивным не является, так как не для всех х имеет место равенство x²+х²=1 (что означает (х, х)Р). Например, при х=0,5 имеем x²+х²=0,51.

Отношение Р симметрично, так как для любых х и уR имеет место цепочка равносильностей (x, y)P  x²+y²=1  y²+x²=1 (так как x²+y²=y²+x²)  (y, x)P, и из (x, y)P следует (y, x)P.

Отношение Р не является транзитивным, так как из (х, y)Р и (y, z)Р не следует (х, z)Р. Действительно, при x=, y=,z= имеем, что (х, y)Р и (y, z)Р (так как x²+y²=1 и y²+z²=1), но (x, z)Р (так как x²+z²=0,51).

Наконец, отношение Р не антисимметрично, так как из (х, y)Р и (y, x)Р не следует х=у (так как из x²+y²=1 и y²+x²=1 не следует х=у).

Ответ: Область определения _Р=х 1х1 =[1, 1].

Область значений _Р=у 1у1 =[1, 1].

Отношение Р не рефлексивно, симметрично, не транзитивно, не антисимметрично.