§2. Отношения. Свойства отношений. Фактор-множество.

2.1. Отношения (См. также [4], §§1.2, 1.5; [5], §1.5). n-местным отношением или n-местным предикатом P на множествах A₁, A₂, …, A_n называется любое подмножество прямого произведения A₁A₂…,A_n. При этом, если (a₁, a₂, …, a_n)P, то говорят что a₁, a₂, …, a_n находятся в отношении Р. Отношение РAⁿ называется n-местным отношением (или n-местным предикатом) на множестве А.

При n=1 отношение называется унарным или свойством. При n=2 отношение называется бинарным или соответствием. При этом если РAB, то говорят о соответствии между множествами A и B, причем, если (a, b)Р, то говорят, что элементу a ставится в соответствие элемент b. В этом случае также пишут aРb.

Пример 2.1. Пусть А=1, 2, 3, 4, 5. Определим бинарное отношение P на А: Р=(a, b)| a меньше b. Тогда Р=(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5). Обратно, задав множество Р перечислением, мы задаём отношение «быть меньше» на множестве А.

Пример 2.2. Пусть А=1, 2, 3, 4, 5, B={a, b}. Определим бинарное отношение P на множествах А и B: Р=(1, a), (2, b), (3, a), (4, b), (5, a). При этом бинарном отношении каждому нечётному числу из А ставится в соответствие буква a, а чётному числу  буква b.

Бинарные отношения на А и B можно изобразить графически.

Первый способ графического изображения назовём декартовым. Он заключается в том, что на двух взаимно перпендикулярных осях отмечаются элементы А и B: на горизонтальной  оси Ох,  элементы А, на вертикальной  оси Оy,  элементы B. Отметив точки с координатами (a, b) такими, что (a, b)Р, получим графическое декартово изображение отношения Р.

Второй способ основан на диаграммах Эйлера-Венна, и заключается в том, что если (a, b)Р, то из a к b проводится стрелка. При этом условимся, что если одновременно (a, b)Р и (b, a)Р, то две стрелки из a к b и из b к a изображать в виде одной двойной (то есть стрелка идёт в обе стороны) (см. рис. 8 ниже)

На рисунках 6 и 7 приведены графические изображения отношений из примеров 2.1 и 2.2.

Тождественным отношением на множестве А называется отношение id_A=(х, х) хА. Универсальным отношением называется отношение U_A=A².

Областью определения бинарного отношения Р называется множество _Р=х(х, y)Р для некоторого у. Областью значений бинарного отношения Р называется множество _Р=у(х, y)Р для некоторого х.

Обратным отношением к бинарному отношению Р называется множество =(у, х)(х, y)Р.

Образом множества Х относительно предиката Р называется множество Р(Х)=у(х, y)Р для некоторого хХ. Прообразом множества Y=Р(Х) относительно предиката Р называется множество (Y)=х(х, y)Р для некоторого уР(Х).

Пример 2.3. Пусть Р  бинарное отношение примера 2.1. Тогда _Р=1, 2, 3, 4=А\{5}, _Р=2, 3, 4, 5=А\{1}, =(2, 1), (3, 1), (4, 1), (5, 1), (3, 2), (4, 2), (5, 2), (4, 3), (5, 3), (5, 4). Пусть Х=3, 4, 5. Тогда Р(Х)=4, 5. Прообразом множества 2, 3 является (2, 3)=1, 2.

Произведением бинарных отношений PAB и QBC (или композицией) называется множество PQ={(x, z)| xA, zC, и существует такой элемент уB что (x, y)P и (y, z)Q}. Произведение PQ также обозначается через PQ.

Пример 2.4. Пусть А=1, 2, 3, 4, 5, B={a, b, с}, С=, , , , Р=(1, a), (2, b), (3, a), (4, b), (5, a), Q =(a, ), (b, ). Тогда PQ =(1, ), (2, ), (3, ), (4, ), (5, ).

Для любых бинарных отношений PAB, QBC, RCD выполняются следующие свойства:

1) PQAC;

2) =P;

3) (PQ)=QP;

4) (PQ)R=P(QR) (ассоциативность произведения);

5) id_AP =P;

6) Qid_BQ =Q;

7) PP=id_A.

Свойство 4) обобщается на произведение любого числа предикатов. Именно, если Р₁А₁А₂, Р₂А₂А₃, …, Р_nА_nА_n+1  предикаты, то в произведении вида (…((Р₁Р₂) Р₃)…)Р_n скобки можно проставлять произвольным образом, это произведение не зависит от расстановки скобок. В связи с этим в произведениях вида (PQ)R и (…((Р₁Р₂)Р₃)…)Р_n скобки принято опускать: (PQ)R=PQR, (…((Р₁Р₂)Р₃)…)Р_n=Р₁Р₂Р₃…Р_n.

Пусть даны два множества А=a₁, a₂, …, a_n, B=b₁, b₂, …, b_m и бинарное отношение PAB. Свяжем с Р матрицу [Р]=(p_ij)_mn, элементы которой определены по следующему правилу:

(p_ij)_mn=

Эта матрица называется матрицей бинарного отношения Р. Она однозначно определяет бинарное отношение.

Пример 2.5. Матрицы бинарных отношений Р и Q из примера 2.4 следующие:

[Р]=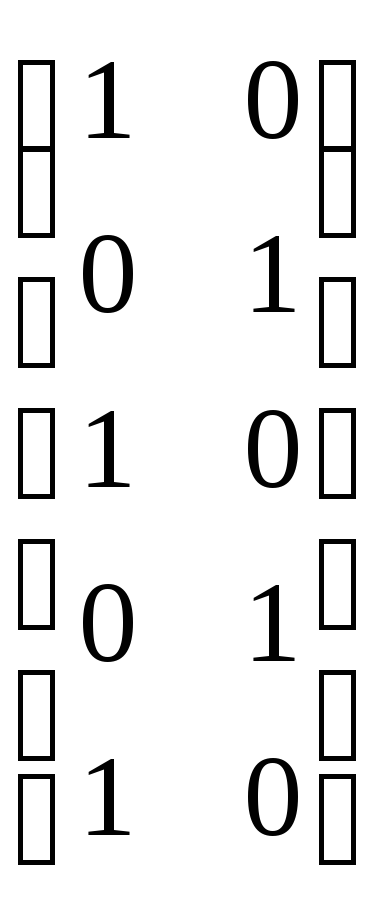, [Q]=.

Матрица бинарного отношения обладает следующими свойствами:

1. Если Р, QAB, [Р]=(p_ij)_mn, [Q]=(q_ij)_mn, то [РQ]=[Р][Q]=(p_ijq_ij)_mn и [РQ]=[Р]+[Q], где сложение производится по правилам 0+0=0, 1+0=0+1=1+1=1, а умножение  по обычным правилам 00=10=01=0, 11=1 (Здесь и далее XY будет означать матрицу, полученную умножением соответствующих элементов матриц X и Y).

2. Если PAB, QBC, то [РQ]=[Р][Q]. Здесь умножение матриц производится по обычным правилам, а произведение и сумма элементов матриц  по правилам, определённым в пункте 1.

3. =[Р]^Т.

4. Если PQ, [Р]=(p_ij)_mn, [Q]=(q_ij)_mn, то [Р][Q] (то есть p_ijq_ij для всех i=1, …, m и j=1, …, n).

5. [id_А]=Е  единичная матрица.

2.2. Свойства отношений. Отношение эквиваленции. Фактор-множество (См. также [4], §§1.5, 1.6; [5], §1.7). Пусть Р  бинарное отношение на А: РА². Отношение называется рефлексивным, если (х, х)Р для всех хА. Это означает, что id_АР, а диагональные элементы матрицы такого отношения равны 1: [Р]=.

Отношение называется симметричным, если для любых х, yА из (х, y)Р следует (y, х)Р. Это означает, что P=Р, то есть [Р]^Т=Р (матрица отношения является симметричной).

Отношение называется антисимметричным, если из (х, y)Р и (y, х)Р следует х=y. Это означает, что РPid_А, то есть в матрице [РP]=[Р][P]^T все элементы, стоящие вне главной диагонали являются нулевыми.

Отношение называется транзитивным, если из (х, y)Р и (y, z)Р следует (х, z)Р. Это означает, что РРР, то есть [РР]=[Р][Р][Р].

Пример 2.6. Отношение Р из примера 2.1 не является ни рефлексивным, ни симметричным, ни антисимметричным, но является транзитивным. Докажем последнее. Так как Р=(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5), то из (1, 2)Р и (2, 3)Р следует (1, 3)Р, из (1, 3)Р и (3, 4)Р следует (1, 4)Р, из (1, 4)Р и (4, 5)Р следует (1, 5)Р, из (2, 3)Р и (3, 4)Р следует (2, 4)Р, из (2, 4)Р и (4, 5)Р следует (2, 5)Р, из (3, 4)Р и (4, 5)Р следует (3, 5)Р.

Это можно увидеть и из соответствующих свойств матрицы отношения. Имеем

[Р]=.

Как видим, не все диагональные элементы равны 1 (точнее, равных 1 среди них вообще нет), что означает не рефлексивность отношения. Далее, матрица отношения не является симметричной, то есть отношение несимметрично. Так как не все элементы вне главной диагонали равны 0, то отношение не является антисимметричным. Наконец,

[РР]=[Р][Р]==,

то есть [РР][Р], и отношение транзитивно.

Отношение, обладающее одновременно свойствами рефлексивности, симметричности и транзитивности, называется отношением эквивалентности (или эквивалентностью). Отношение эквивалентности будем обозначать также через  (знак «тильда»). При этом, если xy, то будем говорить, что x и y эквивалентны.

Пример 2.7. Отношение равенства на множестве чисел является отношением эквивалентности. Действительно, это отношение рефлексивно (для любого хR х=х), симметрично (для любых x, yR из x=y следует y=x) и транзитивно (из x=y и y=z следует x=z).

Пусть на множестве А введено отношение эквивалентности . Тогда множество А разбивается на непересекающиеся между собой подмножества, каждое из которых состоит из эквивалентных между собой элементов, причем неэквивалентные между собой элементы попадают в разные подмножества. Эти подмножества называются классами эквиваленции. Множество всех классов эквиваленции множества А относительно отношения эквивалентности  называется фактор-множеством множества А по  и обозначается через А/. Если отношение эквиваленции обозначить через Р, то соответствующее фактор-множество обозначается через А/Р. Класс, содержащий элемент х, будем обозначать через .

Пример 2.8. Определим на множестве Z целых чисел бинарное отношение по правилу для x, yZ положим x~y тогда и только тогда, когда x и y имеют одинаковую чётность. Это отношение является отношением эквиваленции (проверьте!), и множество Z разбивается на два класса целых чисел  класс четных чисел и класс нечётных чисел.

Если А  множество с конечным числом элементов, на котором введено отношение эквиваленции ~, то элементы А можно пронумеровать таким образом, что матрица отношения ~ будет иметь блочно-диагональный вид с блоками, состоящими из единиц:

[~]=.

Пример 2.9. Рассмотрим отношение Р на множестве А=1, 2, 3, 4, 5, изображённое на рисунке 8: Р=(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3), (4, 4), (4, 5), (5, 4), (5, 5). Оно является одновременно рефлексивным, симметричным и транзитивным (проверьте!), то есть отношение Р  эквиваленция. Её матрица отношений  блочно-диагональноая с двумя блоками из 1:

[Р]=.

2.3. Отношения порядка (См. также [4], §1.7; [5], §1.8). Бинарное отношение РА²=A×A, обладающее свойством рефлексивности и транзитивности, называется отношением предпорядка. Бинарное отношение РА², обладающее свойством рефлексивности, транзитивности и антисимметричности, называется отношением частичного порядка. Таким образом, отношение частичного порядка  это антисимметричный предпорядок. Как правило, отношение частичного порядка обозначается через . Непустое множество А, на котором определён частичный порядок, называется частично упорядоченным.

Частичный порядок А² (напоминаем, что если отношение P  это отношение , то А² означает PА²) называется линейным порядком, если для любых х, yА либо хy, либо yх (то есть любые два элемента х и y из А сравнимы). Непустое множество А, на котором определён линейный порядок, называется линейно упорядоченным. Частично упорядоченное и линейно упорядоченное множества сокращённо обозначаются соответственно через ЧУМ и ЛУМ.

Пример 2.10. Отношение P={(a, a), (b, b), (c, c), (a, b), (b, a), (b, c), (a, c)} на множестве a, b, c обладает свойствами рефлексивности и транзитивности (проверьте!). Значит, это P отношение предпорядка.

Пример 2.11. Отношение P={(a, a), (b, b), (c, c), (b, c)} на множестве А=a, b, c обладает свойствами рефлексивности и транзитивности (проверьте!). Далее, одновременно условия (х, у)Р и (у, х)Р выполняются только для пар (a, a), (b, b), (c, c). Поэтому, если (х, у)Р и (у, х)Р, то х=у. Это означает, что Р удовлетворяет условию антисимметричности. Таким образом, Р рефлексивно, транзитивно и антисимметрично, то есть Р  отношение частичного порядка. При этом оно не является отношением линейного порядка, так как не все элементы множества А сравнимы, а именно, элементы a и b, и элементы a и c. Отношение P={(a, a), (b, b), (c, c), (a, b), (a, c), (b, c)} является отношением линейного порядка.

Пример 2.12. Линейным порядком является любое подмножество действительных чисел относительно обычного отношения . Отношение  на булеане P(А) является частичным порядком, но не линейным (почему?).

Отношение <, определённое по правилу: a<b тогда и только тогда, когда a≤b и a≠b, называется строгим порядком.

Элемент a частично упорядоченного множества A называется максимальным, если для всех xA, сравнимых с a, из a≤x следует, что x=a. Аналогично, элемент a частично упорядоченного множества A называется минимальным, если для всех xA, сравнимых с a, из x≤a следует, что x=a.

Элемент a частично упорядоченного множества A называется наибольшим, если a сравним со всеми элементами из А, и для любого xA имеет место x≤a. Элемент a частично упорядоченного множества A называется наименьшим, если a сравним со всеми элементами из А, и для любого aA имеет место a≤x.

Разница между максимальным и наибольшим элементами (соответственно, между минимальным и наименьшим элементами) очевидна: наибольший элемент является также максимальным, а максимальный элемент, в силу того, что он не обязан быть сравнимым со всеми элементами множества А, вообще говоря, не обязательно наибольший в А. Он является наибольшим только в некотором подмножестве B из A, а именно, в подмножестве тех (и только тех) элементов из A, которые сравнимы с данным максимальным. Ясно, что наибольший элемент во множестве обязан быть единственным: если a и b  наибольшие в A, то с одной стороны, a≤b (так как b  наибольший в A), с другой стоороны b≤a (так как a  наибольший в A), то есть одновременно выполнены условия a≤b и b≤a; но отношение ≤ обладает свойством антисимметричности, и поэтому a=b.

Аналогично, наименьший элемент является минимальным, но обратное, вообще говоря, неверно, и наименьший элемент в частично упорядоченном множестве единствен (докажите!).

Ясно, что в линейно упорядоченном множестве максимальный и наибольший элементы совпадают (соответственно, минимальный и наименьший элементы совпадают).

Максимальный и минимальный элементы не обязательно единственны (почему?).

Максимальный и минимальный элементы множества A будем обозначать через maxA, minA, соответственно. Если их по несколько, то через max₁A, max₂A, …, min₁A, min₂A, ….

Пусть A  ЧУМ и BA. Элемент aA называется верхней гранью множества B, если b≤a для всех bB. Элемент aA называется нижней гранью множества B, если a≤b для любого bB. Из определений верхней и нижней граней множества следует, что они не обязаны принадлежать самому множеству.

Наименьшая из верхних граней множества называется точной верхней гранью (супремумом) данного множества. Наибольшая из нижних граней множества называется его точной нижней гранью (инфимумом). Точная верхняя и нижняя грани множества B обозначаются через supB и infB, соответственно.

Пример 2.13. Рассмотрим интервал [a, b) (a<b) на числовой прямой. Тогда inf [a, b)=a, sup [a, b)=b. Кроме того, для любого c<a имеем, что c  нижняя грань интервала, и для любого d c условием b<d d  верхняя грань.

Пример 2.14. Рассмотрим множество A={, {1}, {2}, {1, 2}} (множество всех подмножеств множества {1, 2}, то есть A=P({1, 2}). Отношение ≤ между элементами введём по правилу a≤b тогда и только тогда, когда ab. Тогда  и {1, 2}  соответственно наименьший и наибольший элементы. В подмножестве B={, {1}, {2}} существует наименьший элемент  это , наибольшего нет; minB=, max₁B={1} и max₂B={2}, то есть в B имеется два максимальных элемента; наконец, infB=, supB={1, 2}.

Аналогично можно рассмотреть minC, maxC, infC, supC, наибольший и наименьший элементы подмножества A={{1}, {2}, {1, 2}} (что предоставляется читателю в качестве несложного упражнения).

2.4. Упражнения. 1. Пусть А=a aN, 1a20. Задать отношение PA² перечислением элементов:

а) (х, у)Р тогда и только тогда, когда х делит у;

б) (х, у)Р тогда и только тогда, когда у=х²;

в) (х, у)Р тогда и только тогда, когда х+у=20;

г) (х, у)Р тогда и только тогда, когда ху делится на 3;

д) (х, у)Р тогда и только тогда, когда ху делится на 5;

е) (х, у)Р тогда и только тогда, когда х+3=у.

Решение. б) В Р включаются такие пары (х, у), что у=х². Например, 4=2². Поэтому (2, 4)P. Так как 83², то (3, 8)P. Окончательно имеем P={(1, 1), (2, 4), (3, 9), (4, 16)}.

Ответ: б) P={(1, 1), (2, 4), (3, 9), (4, 16)}.

2. Пусть A={a, b, c}, B={1, 2, 3, 4}. Изобразить отношения PAB и QB² графически. Найти _Р, _Q, _Р, _Q и РQ:

а) P={(b, 1), (b, 3), (c, 1), (c, 2), (c, 3), (c, 4)}, Q={(1, 1), (2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4), (4, 2), (4, 3), (4, 4)};

б) P={(a, 1), (a, 2), (a, 4), (b, 3), (c, 1), (c, 4)}, Q={(1, 3), (1, 2), (2, 3), (3, 2), (3, 4), (4, 1)};

в) P={(a, 1),(a, 4), (b, 2), (b, 3), (c, 1), (c, 4)}, Q={(1, 1), (1, 4), (2, 1), (3, 4), (4, 3), (4, 1)}.

3. Найти матрицы отношений P, Q из упражнения 2, а также (PQ), и по матрице отношений найти (PQ). С помощью матрицы отношения проверить, является ли отношение Q рефлексивным, симметричным, транзитивным, антисимметричным.

Решение. а) Имеем

[Р]=, [Q]=.

Поэтому по свойствам композиций отношений и их матриц получаем

[(PQ)]=[QP]=[Q][P]=[Q]^T[P]^T==.

В частности, (PQ)=(1, b), (2, b), (3, b), (4, b), (1, с), (2, с, (3, с), (4, с).

Матрица [Q] отношения Q обладает тем свойством, что по главной диагонали стоят единицы. Следовательно, отношение Q рефлексивно.

Далее, матрица [Q] симметрична, [Q]^Т=[Q]. Поэтому отношение Q симметрично.

Так как

[Q][Q]===[Q]

(напоминаем, что умножение матриц и чисел производится обычным образом, а сложение чисел  по правилу 0+0=0, 1+0=0+1=1+1=1, см. свойства матриц бинарных отношений, стр. 12), то отношение Q  транзитивно.

Наконец, вне главной диагонали [Q] имеются ненулевые элементы. Поэтому отношение Q не является антисимметричным.

Таким образом, отношение Q рефлексивно, симметрично, транзитивно (в частности, Q  эквиваленция), не антисимметрично.

Ответ: [Р]=, [Q]=, [(PQ)]=. ОтношениеQ является рефлексивным, симметричным, транзитивным, но не является антисимметричным. (PQ)=(1, b), (2, b), (3, b), (4, b), (1, с), (2, с, (3, с), (4, с).

4. Проверить отношения из упражнения 1 на рефлексивность, симметричность, транзитивность, антисимметричность. Если на множестве А отношение Р является эквиваленцией, то найти фактор-множество .

Решение. г) Так как 0=хх делится на 3 для любого х, то для любого х (х, х)Р, и отношение Р рефлексивно. Далее, для любых х, у из того, что ху делится на 3 следует, что ух=(ху) делится на 3. Поэтому из (х, у)Р следует (у, х)Р, и отношение симметрично. Пусть ху делится на 3 и уz делится на 3. Тогда (в силу того, что сумма чисел, делящихся на 3 тоже делится на 3) хz =(ху)+(уz) делится на 3. Поэтому из (х, y)Р и (y, z)Р следует (х, z)Р, и отношение транзитивно. Следовательно, отношение Р рефлексивно, симметрично, транзитивно, и Р  эквиваленция.

Из того, что ху делится на 3 и ух делится на 3 не следует, что х=у. Поэтому отношение не является антисимметричным.

Найдем фактор-множество по отношению Р. Классами эквиваленции являются =1, 4, 7, 10, 13, 16, 19, =2, 5, 8, 11, 14, 17, 20, =3, 6, 9, 12, 15, 18. Поэтому А/Р=,,.

Ответ: Отношение Р является рефлексивным, симметричным, транзитивным, но не является антисимметричным. А/Р=,,.

5. Найдите область определения, область значений отношения РR². Является ли отношение Р рефлексивным, симметричным, антисимметричным, транзитивным?

а) (x, y)P тогда и только тогда, когда y=|x|;

б) (x, y)P тогда и только тогда, когда xy>1;

в) (x, y)P тогда и только тогда, когда x²+y²=1.

Решение. а) Элемент х может принимать любое действительное значение, то есть хR, и _Р=R. Так как y=|x|0, то _Р=R ₊=у уR, у0  множество всех неотрицательных чисел. Вообще говоря, х|x| (например, 1|1|, и отношение нерефлексивно. Далее, из y=|x| не следует, что х=|у| (это не так, если х  отрицательно), и поэтому отношение несимметрично. Из y=|x| и z=|у| следует z=|x|, так как z=|у|=у=|x| (|у|=у так как y=|x|≥0). Поэтому отношение транзитивно. Наконец, из y=|x| и х=|у| следует х=у, то есть отношение антисимметрично.

Ответ: _Р=R, _Р=R₊=у уR, у0. Отношение нерефлексивно, несимметрично, транзитивно, антисимметрично.

6. Пусть a, b, c, d, e, f  такие числа, что a<b<c<d<e<f, A=[c, d), B=[c, d)(e, f ), C=[a, b)[c, d), D=[c, d)(e, +),E=(,d)[c, d). Найти (в случае наличия) minX, maxX, infX, supX, наименьшее и наибольшее значения множеств X=A, B, C, D, E.

Решение. Решим упражнение для X=B.

Покажем, что minB=с, maxB не существует. Действительно,

B=[c, d)(e, f )={x|c≤x<d}{x|e<x<f }.

Поэтому для xB из x≤c следует, что x=c, так как x удовлетворяет системе неравенств

Следовательно, c=minB. Далее, так как для любого xB имеет место неравенство x<d, то нет такого aB, что для любого xB имело бы место x≤a. Действительно, aB означает, что a<d и тогда существует x такой, что a<x<d, то есть xB и a<x. Следовательно, maxB не существует.

Покажем, что infB=с и supB=f. Будем рассматривать B как подмножество R: BR. Тогда для любого xR с условием x≤y, где y  произвольный элемент из B, является нижней гранью B. Из нижних граней B наибольшим является c, то есть infB=с. Аналогично, любой xR с условием y≤x, где yB, является верхней гранью B. Наименьшая из них  это d, то есть supB=f.

Наконец, в ЛУМ minX и maxX являются одновременно наибольшим и наименьшим элементами, соответственно. Так как B  ЛУМ (как числовое множество) и minB=c, a c=maxB не существует, то наименьшим элементом B является c, а наибольшего элемента не существует.

7. Пусть A={1, 2, 3} (A={1, 2, 3, 4}) и P(A)  его булеан.

а) Доказать, что P(A) имеет наименьший и наибольший элементы относительно отношения . Найти все минимальные и максимальные элементы в P(A).

б) Для B=P(A)\{{2, 3}, {1, 2, 3}} найти наибольший и наименьший элементы, minB, maxB, infB, supB (если указанные элементы существуют).

в) Изобразить графически отношение  на A, B.