
ФИЗИКА Ч1 / Лекции_Постников / 1_1
.pdf
2
2.5.Общее решение этого уравнения имеет вид
s = A1 sin ωt + A2 cosωt
где А1 и А2 определяются из начальных условий
A |
= |
|
1 ds |
|
|
и |
A = s(0) |
|||
|
|
|
|
|
|
|
||||
|
|
|
||||||||
1 |
|
ω dt |
|
t =0 |
|
2 |
||||
|
|
|
|
|
||||||
2.6. Общее решение может быть приведено к стандартному виду s = Asin(ωt +ϕ0 )
где A =  A12 + A22 и ϕ0 = arctg(A2
A12 + A22 и ϕ0 = arctg(A2  A1 )
A1 )
2.7.Графическое представление гармонических колебаний
2.8.Согласно формуле Эйлера
eiϕ = cosϕ +i sinϕ
Поэтому формулу гармонических колебаний можно запи-
сать в комплексном виде |
|
|||||
|
|
|
~ |
~ iωt |
= Ae |
i(ωt +ϕ1 ) |
|
~ |
|
s |
= Ae |
|
|
где |
iϕ |
- |
комплексная амплитуда, а физический |
|||
A = Ae |
1 |
|||||
смысл имеет только действительная часть комплексной функции
Re ~s = s = Acos(ωt +ϕ1 ) = Asin(ωt +ϕ0 )
3.Колебания материальной точки вдоль оси X около положения равновесия описываются уравнением движения
x= Asin(ωt +ϕ0 )
3.1.Проекция скорости и ускорения на ось Х
vx = v0 cos(ωt +ϕ0 ) |
и |
|
ax |
= −a0 sin(ωt +ϕ0 ) |
где v = Aω - амплитуда скорости, a |
0 |
= Aω2 |
= v ω - амплитуда ускорения |
|
0 |
|
|
0 |
|
3.2. Движущая сила колебаний |
|
|
F = −mω2 x |
|
F = m a |
и |
|
||
подобна упругой силе |
|
|
x |
|
Fx |
= kx |
|
||
|
|
|||
(силы иной физической природы, удовлетворяющие тому же виду зависимости, на-
зываются квазиупругими силами).
3.3.Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна
W |
= |
mv2 |
= |
mv2 |
cos2 (ωt +ϕ |
) = |
mω2 A2 |
cos2 (ωt +ϕ |
) |
|
0 |
|
|||||||
|
|
|
|||||||
к |
2 |
|
2 |
0 |
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|||
или
Wк = mω42 A2 [1+cos(2ωt +2ϕ0 )]
3.4.Потенциальная энергия материальной точки, гармонически колеблющейся под действием квазиупругой силы, равна
|
Wп = −∫x |
Fx dx = |
mω2 x2 |
= |
mω2 A2 |
sin2 (ωt +ϕ0 ) |
|
|
||||
|
|
2 |
|
|
||||||||
|
|
0 |
|
|
2 |
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
W = |
mω2 A2 |
[1−cos(2ωt +2ϕ |
)]=W = |
mω2 A2 |
[1+cos(2ωt +2ϕ |
0 |
+π)] |
|||||
|
|
|||||||||||
п |
4 |
|
0 |
|
к |
4 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
3.5.Колебания потенциальной и кинетической энергии совершаются со сдвигом по фазе на π, так что полная механическая энергия материальной точки

3
W=Wп +Wк = mω22 A2 = const
4.Линейный гармонический осциллятор – материальная точка массы m, совершающая прямолинейные гармонические колебания под действием упругой силы (например, пружинный маятник с коэффициентом жесткости пружины k). Уравнение движения имеет вид
m |
d 2 x |
= −kx |
или |
d 2 x |
+ |
k |
x = 0 |
||
dt |
2 |
dt2 |
m |
||||||
|
|
|
|
|
|||||
т.е. точка совершает колебания с частотой и периодом |
|
|
|
||||||
ω = k m |
и |
T = 2π m k |
|||||||
Потенциальная энергия линейного гармонического осциллятора
= kx2 Wп 2
5.Физический маятник – твердое тело, имеющее возможность качаться под действием силы тяжести вокруг неподвижной оси, не проходящей через центр тяжести тела и называемой осью качания. Точка пересечения оси качания с плоскостью, проходящей через центр тяжести маятника (центр масс твердого тела) и перпендикулярная оси качания, называется точкой подвеса. Уравнение движения (в отсутствие сил трения)
Jd 2α2 = −mgd sinα dt
где α - угол поворота маятника вокруг оси качания из положения равновесия; d – расстояние от центра масс маятника до точки подвеса; J – момент инерции маятника относительно той же оси; m – масса маятника. При малых колебаниях sinα =α и
d 2α |
+ |
mgd |
α = 0 |
|
dt 2 |
J |
|||
|
|
Таким образом
α =α0 sin(ωt +ϕ0 )
где α0 – амплитуда колебаний, а циклическая частота и период колебаний
ω = mgd J и |
T = 2π J mgd |
6.Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести.
6.1. Момент инерции
J = ml2
6.2.Циклическая частота
ω= g l
6.3.Период малых колебаний (изохронные колебания)
T = 2π l g
7.Приведенной длиной физического маятника называется длина математического маятника, имеющего такой же период колебаний
lпр = mdJ = d + mdJC > d

Лекция 8
СЛОЖЕНИЕ КОЛЕБАНИЙ
Сложение параллельных колебаний. Биения. Сложение колебаний разных частот. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
Свободные затухающие колебания. Период и коэффициент затухания, время релаксации, декремент затухания.
1.Под сложением колебаний понимают нахождение закона результирующих колебаний системы в тех случаях, когда система участвует одновременно в нескольких колебательных процессах.
1.1.Два предельных случая – колебания в одном направлении и взаимно перпендикулярные.
1.2.Сложение двух одинаково направленных гармонических колебаний
s1 = A1 sin(ω1t +ϕ1 ) и |
s2 = A2 sin(ω2t +ϕ2 ) |
производится методом векторных диаграмм.
1.3.Проекция результирующего вектора A(t) на вертикальную
ось
s = A(t) sin Ф(t)
1.4.Амплитуда и фаза может быть найдена по теореме косинусов
[A(t)]2 = A12 + A22 +2A1 A2 cos[Ф2 (t) −Ф1 (t)]
tgФ(t) = |
A1 sin Ф1 |
(t) + A2 sin Ф2 (t) |
|||
A cosФ |
(t) + A cosФ (t) |
||||
|
|||||
|
1 |
1 |
2 |
2 |
|
2.Если разность фаз складываемых колебаний не зависит от времени, то такие колебания называются когерентными
d |
[Ф (t) −Ф (t)] ≡ 0 и |
Ф (t) −Ф (t) = const |
||
|
||||
dt |
2 |
1 |
2 |
1 |
|
|
|
|
|
2.1.Из этого следует
|
|
ω1 =ω2 =ω |
|
и |
s = s1 + s2 = Asin(ωt +ϕ0 ) |
|||||
где A2 = A2 |
+ A2 |
+2A A cos(ϕ |
2 |
−ϕ |
) и tgϕ |
0 |
= |
A1 sinϕ1 |
+ A2 sinϕ2 |
|
|
|
|||||||||
1 |
2 |
1 |
2 |
1 |
|
|
A1 cosϕ1 |
+ A2 cosϕ2 |
||
|
|
|
|
|
|
|
|
|
||
р– р
2.2.Амплитуда изменяется в пределах
от А = |А1 - А2| при ϕ2 - ϕ1 = ±(2m + 1)π (колебания в противофазе)
до А = А1 + А2 при ϕ2 - ϕ1 = ±2mπ (синфазные колебания) где m = 0, 1, 2, … любое целое неотрицательное число.
3.Если частоты складываемых колебаний различны, то такие колебания некогерентны. Но два гармонических колебания с различными циклическими частотами можно прибли-
женно считать когерентными в течение некоторого промежутка времени t, за который разность фаз этих колебаний изменяется незначительно
ω2 −ω1 t << 2π или t <<τког
где τког = 2π ω2 −ω1 – время когерентности рассматриваемых колебаний.
ω2 −ω1 – время когерентности рассматриваемых колебаний.
4.В результате сложения двух одинаково направленных гармонических колебаний с близкими частотами ( ω2 −ω1 <<ω1 ) возникают биения.
4.1.За начало отсчета времени лучше всего взять момент, когда фазы складываемых колебаний совпадают и равны ϕ0
s1 = A1 sin(ω1t +ϕ0 ) и |
s2 = A2 sin(ω2t +ϕ0 ) = A2 sin(ω1t +ϕ0 +ϕ(t)) |
где ϕ(t) = (ω2 −ω1 )t |
|

2
4.2.Результирующие колебания удовлетворяют соотношениям
|
|
|
|
s = s1 + s2 |
= A(t) sin[ω1t +ϕ0 +ψ(t)] |
||||
где [A(t)]2 |
= A2 |
+ A2 |
+2A A cosϕ(t) и tgψ(t) = |
|
A2 sinϕ(t) |
|
|||
|
|
||||||||
|
1 |
|
2 |
1 |
2 |
|
A1 |
+ A2 cosϕ(t) |
|
|
|
|
|
|
|
|
|||
4.3. Величина |
A(t) |
называется |
амплитудой биений и изменяется в пределах |
||||||
от А=|А1 - А2| до А = А1 + А2 с циклической частотой Ω = ω2 −ω1 , называемой цик-
лической частотой биений.
4.4.Период и частота биений
T = |
2π |
= |
|
2π |
|
= |
|
1 |
и |
ν |
Б |
= |
1 |
= |
|
ν |
|
−ν |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
Б |
Ω |
|
ω |
2 |
−ω |
1 |
|
1 T −1 T |
|
|
|
T |
|
|
|
2 |
|
1 |
||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
1 |
|
|
|
|
Б |
|
|
|
|
|
|
||
5.При сложении гармонических колебаний, совпадающих по направлению и имеющих кратные циклические частоты, получаются периодические негармонические колебания с периодом T = 2π ω .
ω .
5.1.Любое сложное периодическое колебание можно представить в виде суммы гармонических колебаний с циклическими частотами, кратными основной циклической частоте ω = 2π T
T
s =
где
an =
bn =
|
|
a0 |
∞ |
|
a0 |
∞ |
|
f (t) = |
+∑(an cos nωt +bn sinnωt) = |
+∑An sin(nωt +ϕn ) |
|||||
|
|
||||||
|
2 |
n=1 |
2 |
n=1 |
|||
2 |
T 2 |
|
|
|
|
||
∫ f (t) cos nωtdt |
n = 0,1, 2, ... |
|
|||||
T |
|
||||||
−T 2 |
|
|
|
|
|||
2 |
T 2 |
|
|
|
|
||
∫ f (t) sin nωtdt |
n =1, 2, ... |
|
|||||
T |
|
||||||
−T 2 |
|
|
|
|
|||
5.2.Такое представление периодической функции называется разложением этой функции в ряд Фурье, а члены ряда с частотами ω, 2ω, 3ω и т.д. называются гармониками. Совокупность гармоник образует спектр колебания.
6.При сложении взаимно перпендикулярных колебаний одинаковой частоты
x = A1 sin(ωt +ϕ1 ) |
и |
|
|
y = A2 sin(ωt +ϕ2 ) |
|||||||||||||
уравнение траектории движения точки можно записать в виде |
|
||||||||||||||||
|
x2 |
+ |
|
y2 |
− |
2xy |
cos(ϕ |
|
−ϕ |
) = sin |
2 |
(ϕ |
|
−ϕ |
) |
||
|
A2 |
A2 |
A A |
|
|
|
|||||||||||
|
|
|
|
|
2 |
1 |
|
|
|
2 |
1 |
|
|||||
1 |
|
|
|
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
Такие колебания называются эллиптически поляризованными. |
|||||||||||||||||
6.1. При ϕ2 −ϕ1 = (2m +1) |
π |
траектория движения точки превращается в окружность |
|||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + y2 =1
A12 A22
и такие колебания называют циркулярно поляризованными колебаниями.
6.2.При ϕ2 −ϕ1 = mπ траектория движения точки вырождается в отрезок прямой
y = ± A2 x A1
итакие колебания называются линейно поляризованными колебаниями.
7.Затухающие колебания – колебания, амплитуды которых из-за потерь энергии в реальных механических системах уменьшаются с течением времени. Если параметры, определяющие физические свойства системы, в процессе колебаний не изменяются, то такие системы называются линейными.

3
7.1.Дифференциальное уравнение свободных затухающих колебаний линейной системы
d 2 s |
|
ds |
2 |
|
|
+2β |
|
+ω0 s = 0 |
|
dt2 |
dt |
|||
|
|
где β - коэффициент затухания.
7.2.Решение этого уравнения в общем виде
s = exp{−βt}u(t) |
или s = A0 exp{−βt}cos(ωt +ϕ) |
где A = A0 exp{−βt} – амплитуда затухающих колебаний, а ω2 =ω02 − β2 .
7.3.Промежуток времени τ =1 β , в течение которого амплитуда уменьшается в е раз,
β , в течение которого амплитуда уменьшается в е раз,
называется временем релаксации.
7.4.Затухание нарушает периодичность колебаний, но при малых затуханиях период затухающих колебаний можно определить по формуле
T = 2π ω = 2π  ω02 − β2
ω02 − β2
7.5.Отношение амплитуд двух последовательных колебаний, по времени отличающихся на величину периода,
A(t) |
= exp{βT} |
|
A(t +T ) |
||
|
называется декрементом затухания, а логарифм этого отношения
= ln |
A(t) |
= βT = |
T |
= |
1 |
|
A(t +T ) |
τ |
Ne |
||||
|
|
|
где Ne – число колебаний, совершаемых за время уменьшения амплитуды в е раз,
называется логарифмическим декрементом затухания.
7.6.Для характеристики колебательной системы вводится понятие добротности (при
β2 <<ω02 )
Q = π =πNe = βπT0 = 2ωβ0

Лекция 9
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ВОЛНОВОЕ ДВИЖЕНИЕ
Вынужденные колебания. Резонанс.
Волновое движение. Уравнение плоской незатухающей бегущей волны. Энергия упругой волны. Вектор плотности потока энергии. Сложение (интерференция) волн. Стоячие волны
1.Переменная внешняя сила, приложенная к колебательной системе и вызывающая в ней механические колебания, называется вынуждающей (возмущающей) силой.
2.Дифференциальное уравнение вынужденных колебаний
d 2 x |
+2β |
dx |
+ω2 x = |
1 |
F (t) |
|
dt2 |
dt |
m |
||||
|
0 |
x |
3.Если Fx (t) - периодическая функция, то после приложения этой силы к маятнику возни-
кает переходный режим вынужденных колебаний
x = x1 (t) + x2 (t)
где первый член соответствует свободным затухающим колебаниям
x (t) = A e−βt sin(ωt +ψ |
0 |
) |
ω = ω2 |
− β2 |
|
1 |
0 |
|
0 |
|
|
а второй член соответствует незатухающим периодическим колебаниям с частотой, равной частоте возмущающей силы
4. Амплитуда свободных затухающих колебаний A0e−βt быстро уменьшается и через некоторое время (τ0 = 4,6 β , когда уменьшение происходит в 100 раз)) свободные колебания
β , когда уменьшение происходит в 100 раз)) свободные колебания
маятника практически прекращаются
x(t) ≈ x2 (t)
Такое состояние называется режимом установившихся вынужденных колебаний. 5. Если возмущающая сила изменяется по периодическому закону
Fx = F0 cos Ωt
то установившиеся вынужденные колебания будут совершаться с такой же частотой x = Acos(Ωt +ϕ0 )
где
F0 |
|
|
|
|
|
|
|
|
|
|
|
2βΩ |
|
A = m (ω02 −Ω2 )2 +4β2Ω2 |
|
|
и |
tgϕ0 = − |
|
|
|||||||
|
ω02 −Ω2 |
||||||||||||
При Ω = 0 сдвиг фаз ϕ0 = 0 и A = |
F0 |
|
= |
|
F0 |
|
- статическое смещение маятника из положения |
||||||
mω02 |
|
|
k |
||||||||||
равновесия. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Максимального значения амплитуда вынужденных колебаний достигает при |
|||||||||||||
|
|
Ωp = |
ω02 −2β2 |
|
|
|
|||||||
Такая частота колебаний называется резонансной, максимальная амплитуда равна |
|||||||||||||
|
A |
p |
= |
|
|
|
F0 |
= |
πF0 |
|
|
|
|
|
|
2mβω |
mδω2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
где ω = ω02 − β2 - циклическая частота свободных затухающих колебаний, δ - логарифми-
ческий декремент затухания. 7. При малых значениях β
Ωp ≈ω0 , ϕ0 (Ωp ) ≈ −π 2, Ap ≈ QA0
2, Ap ≈ QA0
где Q ≈π δ - добротность маятника, A0 = x0
δ - добротность маятника, A0 = x0  ω02 - величина статического смещения.
ω02 - величина статического смещения.

2
8.При установившихся вынужденных колебаниях действие диссипативных сил компенсируется действием возмущающей силы, которая совершает работу, равную работе сил сопротивления.
T |
dx 2 |
2 |
|
2 T |
2 |
2 |
2 |
||
Aсопр = −b∫ |
|
|
dt = −2mβA |
Ω |
∫sin |
|
(Ωt +ϕ0 )dt = −mβA |
Ω T |
|
|
|
||||||||
0 |
dt |
|
|
0 |
|
|
|
||
где b = 2mβ - коэффициент сопротивления.
Aвозм = F0 T∫ |
dx |
cos Ωtdt = −AΩF0 T∫cos Ωt sin(Ωt +ϕ0 )dt = − |
1 |
AΩF0T sinϕ0 = −Aсопр |
|
2 |
|||
0 dt |
0 |
|
||
Волновое движение
9.Процесс распространения колебаний в сплошной среде называется волновым процессом.
10.Основное свойство волнового процесса – перенос энергии в пространстве без переноса вещества.
11.Геометрическое место точек, до которого доходят колебания к моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью (в простейших случаях – плоские и сферические волны).
12.Два типа волн – продольные и поперечные. Два вида волн – бегущие и стоячие.
13.Бегущая волна переносит энергию в пространстве. Количественно перенос энергии ха-
рактеризуется вектором плотности потока энергии.
14.Уравнение бегущей волны (на примере плоской волны)
ξ(x,t) = Asin ω(t − x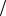 v)
v)
В общем случае распространение плоской волны в среде, не поглощающей энергию, имеет вид
ξ(x,t) = Asin[ω(t − x v) +ϕ0 ]
v) +ϕ0 ]
15. Для характеристики волн используется волновое число k = 2λπ = 2vTπ = ωv
Тогда уравнение плоской волны можно записать в виде
ξ(x,t) = Asin(ωt −kx +ϕ0 ) |
или |
ξ(x,t) = Ae−i(ωt−kx+δ ) |
||||
где δ =ϕ0 −π 2 и имеет смысл только реальная часть комплексного числа. |
||||||
16. Если фаза волны постоянна (ω(t − x v) +ϕ0 |
= const ), то после дифференцирования будет |
|||||
ω(dt − |
1 |
dx) = 0 |
или |
|
dx |
= v |
|
|
|||||
|
v |
|
|
dt |
||
что позволяет определить скорость v, как скорость распространения фазы волны, или фазо-
вую скорость.
v = ωk
17.Для сферической волны (r значительно больше размера источника волн)
ξ(r,t) = Ar sin(ωt −kr +ϕ0 )
18.В общем случае распространение волн в изотропной среде описывается дифференциаль-
ным уравнением – волновым уравнением
d 2ξ |
+ |
d 2ξ |
+ |
d 2ξ |
= |
1 d 2ξ |
или |
ξ = |
1 d 2ξ |
|||||
|
|
|
|
|
|
|
|
|
||||||
dx2 |
dy2 |
dz2 |
v2 dt2 |
v2 dt2 |
||||||||||
|
|
|
|
|
||||||||||
19. Фазовая скорость механических волн в упругой среде

3
v = K ρ
где ρ - плотность среды, К – модуль объемной упругости среды.
Фазовая скорость поперечных упругих волн в однородной изотропной твердой среде v = G ρ
Фазовая скорость продольных упругих волн в однородной изотропной твердой среде v = E ρ
где Е и G – соответственно модули упругости и сдвига материала.
20.При распространении волн в упругой среде ее кинетическая энергия обусловлена коле-
бательным движением частиц среды, а потенциальная энергия – деформацией.
21.Объемная плотность кинетической энергии среды
wк = dWdVк = 12 ρv12
где v1 – скорость частиц среды, dWк - кинетическая энергия всех частиц в малом объеме dV ,
в пределах которого скорость частиц одинакова.
22. Объемная плотность потенциальной энергии упруго деформированной среды wп = dWdVп = 12 ρv2ε2
где v – фазовая скорость волны в среде; ε - относительная деформация; dWп - потенциальная энергия однородно деформированной среды.
23. |
Объемная плотность энергии упругих волн |
|
|
|
|
|
|
||||||||
|
|
|
|
w = w + w = |
1 |
|
ρ(v2 |
+v2ε2 ) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
п |
к |
2 |
|
1 |
|
|
|
|
|
24. |
Для плоской продольной бегущей волны |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
v = |
ds |
|
ds |
v |
|
|
|
w = w |
w = ρv2 |
ds 2 |
||||
|
|
ε = |
|
= − |
1 |
|
|
|
= ρ |
|
|
||||
|
|
|
|
|
|
|
|||||||||
|
1 |
dt |
|
dx |
v |
|
|
п |
к |
1 |
dt |
||||
|
|
|
|
|
|
|
|
||||||||
25. |
Для плоской бегущей синусоидальной волны |
|
|
|
|
|
|
||||||||
w = ρA2ω2 cos2 (ωt −kr +ϕ0 )
для сферической
w= ρ a0 2ω2 cos2 (ωt −kr +ϕ0 )
r
исреднее за период значение объемной плотности энергии упругих волн
w= 12 ρA2ω2
26.Скорость переноса энергии волной равна скорости перемещения в пространстве поверхности, соответствующей максимальному значению объемной плотности энергии волны.
27.Потоком энергии называется величина
dФw dS = dWdt
где dW = wvdtdS cosα = w(v d S)dt - величина энергии, передаваемой через площадку dS за
малый промежуток времени, v – вектор скорости переноса энергии волной, α - угол между вектором скорости и нормалью к площадке dS.
Тогда
dФw dS = w(v d S) = (U d S)
где U = w v – называется вектором Умова (вектором плотности потока энергии волны).
28.Интенсивностью волны (для бегущей плоской синусоидальной волны) называется модуль среднего значения вектора Умова

|
4 |
|
|
I = |
U = v w = |
1 |
ρvω2 A2 |
|
|
2 |
|
29.Поглощение волн происходит главным образом за счет процессов внутреннего трения и теплопроводности. Для амплитуды и интенсивности можно записать
A(x) = A e−αx |
и |
I (x) = I |
e−2αx |
0 |
|
0 |
|
где А0 и I0 – амплитуда и интенсивность в точке x = 0, α - линейный коэффициент поглощения упругих волн.
30. Принцип суперпозиции волн
n |
n |
n |
s = ∑si |
v = ∑vi |
a = ∑ai |
i=1 |
i=1 |
i=1 |
31. Волновой пакет – суперпозиция волн, мало отличающихся друг от друга по амплитуде и частоте, занимающая в каждый момент времени ограниченную часть пространства
В простейшем случае наложения двух синусоидальных волн с одинаковой амплитудой
s= A0 sin(ωt −kx) + A0 sin[(ω +dω)t −(k +dk)x] = 2A0 cos tdω − xdk sin(ωt −kx)
2
возникает псевдосинусоидальная волна с амплитудой
A = 2A0 cos tdω − xdk2
За скорость распространения этой волны принимается скорость перемещения максимума амплитуды волны. Если tdω − xdk = const , то
dxdt = ddkω = u (групповая скорость)
u = v −λ |
dv |
(связь групповой скорости с фазовой скоростью) |
|
dλ |
|||
|
|
32.Если разность фаз двух волн не зависит от времени, то такие волны называются коге-
рентными.
33.Интерференцией волн называется явление наложения волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других в зависимости от соотношения между фазами этих волн.
34.При наложении когерентных сферических волн
s1 = A1 sin(ωt −kr1 +ϕ1 ) = A1 sin Ф1 и |
s2 = A2 sin(ωt −kr2 +ϕ2 ) = A2 sin Ф2 |
амплитуда и фаза результирующих колебаний в точке М
A2 = A12 + A22 +2A1 A2 cos[k(r2 −r1 ) −(ϕ2 −ϕ1 )]
tgФ = A1 sin Ф1 + A2 sin Ф2 A1 cosФ1 + A2 cosФ2
Так как для когерентных волн ϕ2 −ϕ1 = const , то интерференция зависит от величины
= r2 −r1
которая называется разностью хода.
35. Максимумы интерференции удовлетворяют условию k −(ϕ2 −ϕ1 ) = ±2mπ
где m = 0, 1, 2,… – порядок интерференционного максимума.
Условие интерференционных минимумов
k −(ϕ2 −ϕ1 ) = ±(2n −1)π
где n = 1, 2, 3,… – порядок интерференционного минимума.
36.Частный случай интерференции волн – стоячие волны, которые образуются при наложении двух бегущих навстречу друг другу синусоидальных волн, имеющих одинаковые частоты и амплитуды
s1 = Asin(ωt −kx) и |
s2 = Asin(ωt +kx +α) |
5
где α - разность фаз в точках х = 0. В этом случае образуется стоячая волна
s = s1 + s2 |
|
α |
|
α |
||
= 2Acos kx + |
2 |
sin ωt + |
2 |
|
||
|
|
|
|
|
||
37.Точки, в которых амплитуда стоячей волны равна нулю, называются узлами стоячей волны, а точки, в которых амплитуда максимальна, называются пучностями.
kx + |
α |
= (2m +1) π |
(узлы) |
|||
|
2 |
|
|
|
2 |
|
kx +α |
= mπ |
(пучности) |
||||
38. Длина стоячей волны |
|
2 |
|
|
|
|
|
|
|
|
= λ |
|
|
|
|
|
λ |
ст |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
где λ - длина бегущей волны.
