ФИЗИКА Ч1 / Лекции_Постников / 1_1

Лекция 1

КИНЕМАТИКА

Системы отсчета. Кинематика материальной точки. Траектория, перемещение, путь, скорость, ускорение. Равномерное и равнопеременное прямолинейное движение. Криволинейное движение; нормальное и тангенциальное ускорения. Движение точки по окружности. Угловые перемещение, скорость, ускорение. Связь линейных и угловых характеристик. Кинематика абсолютно твердого тела (АТТ), число степеней свободы.

1.Механическое движение – изменение взаимного расположения тел или их частей в пространстве с течением времени.

1.1.В зависимости от величины и скорости перемещения объектов механика подразделя-

ется на классическую, релятивистскую и квантовую.

1.2.Классическая механика состоит из трех основных разделов – статики, кинематики и динамики.

1.2.1.Статика – рассматривает законы сложения сил и условия равновесия тел.

1.2.2.Кинематика – дает математическое описание всевозможных видов механического движения безотносительно к тем причинам, которые вызывают эти движения.

1.2.3.Динамика – исследует влияние взаимодействия между телами на их механическое движение.

1.3.Материальная точка – тело, форма и размеры которого несущественны в условиях данной задачи. Система материальных точек – совокупность тел или частей одного тела, каждая из которых удовлетворяет понятию материальной точки.

1.4.Абсолютно твердое тело – тело, деформацией которого в условиях данной задачи можно пренебречь. Абсолютно упругое тело – тело, деформация которого подчиняется закону Гука. Абсолютно неупругое тело – тело, которое после прекращения внешнего воздействия полностью сохраняет деформированное состояние, вызванное этим воздействием.

2.Системой отсчета называется жестко связанная с абсолютно твердым телом система координат, снабженная часами и используемая для определения положения в пространстве тел и их частей в различные моменты времени.

2.1.Тело, с которым связана система отсчета, называют телом отсчета.

2.2.Чаще всего употребляется декартова система координат, ортонормированный ба-

зис которой образованG G тремя единичными по модулю и взаимно ортогональными векторами i , j и k , проведенными из начала координат.

2.3.Положение материальной точки задается радиус-вектором Gr, соединяющим начало координат с этой точкой – r = x i + y j + z k , где x i , y j , z k – компоненты радиус-

вектора по координатным осям, а x, y, z – декартовы координаты материальной точки.

3.Движение материальной точки определяется кинематическими уравнениями движения материальной точки – x = x(t), y = y(t), z = z(t), которые эквивалентны векторному уравнению движения материальной точки – r = r(t).

3.1.Линия, описываемая в пространстве движущейся точкой, называется траекторией движения этой точки.

3.2.В зависимости от формы траектории различают прямолинейное и криволинейное движения точки. В общем случае траектория материальной точки – пространст-

венная кривая.

3.3.Сумма длин всех участков траектории, пройденных материальной точкой за рассматриваемый промежуток времени, называется длиной пути.

3.4.Момент времени t = t0, ранее которого движение точки не рассматривается, называется начальным моментом времени (обычно полагают t0 = 0), а положение точки в пространстве в этот момент называется начальным положением.

2

3.5. Вектором перемещения точки за промежуток времени от t = t1 до t = t2 называется вектор, проведенный из положения точ-

ки в момент t1 в ее положение в момент t2 rG2 - rG1 = rG(t2 ) – r (t1 )

4.Число независимых движений, которые может совершать механическая система, называется числом степеней свободы.

4.1.Материальная точка, свободно движущаяся в пространстве, может совершать только три независимых движения (три степени свободы) – поступательное движение вдоль координатных осей.

4.2.Система материальных точек помимо поступательного движения может совершать вращательное движение всей системы и колебательное движение элементов системы относительно друг друга. Таким образом, система материальных точек име-

ет девять степеней свободы.

5.Скорость – характеристика быстроты движения тел.

5.1. Средней скоростью движущейся точки в интервале времени от t до t + t называется вектор vср , равный отношению приращения радиус-вектора r за этот промежу-

ток времени к его продолжительности.

vср = r / t

5.2. Скоростью (или мгновенной скоростью) точки называется векторная величина v , равная первой производной по времени от радиус-вектора r рассматриваемой точки v = d r /dt

5.3. Вектор скорости направлен по касательной к траектории в сторону движения материальной точки.

5.4. Разложение вектора v по базису декартовой системы координат имеет вид vG = vx i +vy j + vz k

Модуль вектора скорости равен

Движение точки называется равномерным, если модуль скорости ее перемещения остается неизменным

v = const

5.5.Средней путевой скоростью неравномерного движения называется скалярная ве-

личина, равная отношению длины пройденного участка траектории к продолжительности прохождения этого участка. В общем случае средняя путевая скорость точки не равна модулю средней скорости точки на этом участке

vср = vср

5.6.При плоском движении материальной точки ее скорость v можно разложить на две составляющие – радиальную скорость vr и трансверсальную скорость vϕ

v = vr +vϕ

единичный вектор, направленный перпендикулярно плоскости движения точки. Модуль вектора скорости при этом

5.7.При вращении тела вокруг оси отдельные точки тела двигаются с угловой скоростью ω, вектор которой направлен вдоль оси вращения по правилу правого винта, а модуль не зависит от положения точки относительно оси

ω= ddtϕ

6.Ускорение – характеристика быстроты изменения скорости.

6.1.Ускорением называется векторная величина a , равная первой производной по

времени от скорости v материальной точки

6.1.1.Если dvdt > 0 , то движение называется ускоренным, а если dvdt < 0 , то движение называется замедленным.

6.1.2.Если dvdt = const , то движение называют равнопеременным: при dvdt > 0 - рав-

ноускоренное движение; при dvdt < 0 - равнозамедленное движение.

6.1.3.Путь, пройденный телом при равноускоренном (равнозамедленном) движении определяется уравнением

s = s0 +v0t + at 2

2

6.1.4.Мгновенное значение скорости при равноускоренном (равнозамедленном) движении определяется выражением

v= v0 +at

6.2.Вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории. Его можно разложить на две составляющие – касательное,

или тангенциальное, ускорение aτ и нормальное, или центростремительное, ус-

корение an

a= aτ +an

6.2.1.Вектор тангенциального ускорения направлен параллельно вектору скорости (по касательной к траектории движения), а его модуль равен первой производной от скорости по времени

aτ = dvdt

6.2.2.Вектор нормального ускорения направлен перпендикулярно вектору тангенциального ускорения (в направлении, противоположном направлению вектора радиуса кривизны траектории), а его модуль определяется соотношением

an = v2 R

6.2.3. Модуль полного ускорения определяется выражением a = aτ2 +an2

6.3.Тангенциальное и нормальное ускорения определяются характером движения.

6.3.1.Признаком прямолинейного движения является an = 0 .

6.3.2.Признаком равномерного движения является aτ = 0 .

4 6.3.3. Для наиболее распространенных видов движения

7. Вращательное движение описывается уравнением движения, в котором характеристи-

кой перемещения тела в пространстве является угол поворота ϕ

ϕ = ϕ(t)

7.1. При вращении тела вокруг оси отдельные точки тела двигаются с угловой скоростью ω, вектор которой направлен вдоль оси вращения по правилу правого винта, а модуль равен первой производной от угла вращения по времени

ω = ddtϕ

7.2. Если ω = const, то вращение равномерное и его характеризуют периодом вращения Т – временем, за которое любая точка тела совершает один полный оборот.

T = 2ωπ

7.3. Число полных оборотов в единицу времени называется частотой вращения n =1T =ω(2π )

7.4. Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени

ε = ddtω

7.4.1. Угол поворота при равноускоренном (равнозамедленном) вращательном движении определяется уравнением

ϕ =ϕ0 +ω0t + εt 2

2

7.4.2.При ускоренном вращательном движении мгновенное значение угловой скорости определяется выражением

ω=ω0 +εt

7.4.3.При увеличении скорости вращения направление вектора углового ускорения совпадает с направлением вектора угловой скорости, а при уменьшении скорости вращения направление вектора углового ускорения противоположно направлению вектора угловой скорости.

8.Связь между линейными (длина пути s, модуль линейной скорости v, модули ускорений

аτ и аn) и угловыми характеристиками (угол поворота φ, угловая скорость ω, угловое ускорение ε)

s = Rϕ v =ωR

3

7.2.При любых процессах, происходящих в замкнутой системе, скорость ее центра

масс не изменяется

vC = const

8.Внутри замкнутой системы могут действовать постоянные силы разного происхождения

– трения, упругости, тяготения.

8.1.Силы трения бывают двух типов – внешнее и внутреннее трение.

8.2.Внешнее трение возникает в плоскости соприкасания двух тел при их относитель-

ном перемещении (трение скольжения, трение качения).

8.3.Внутреннее трение происходит между частями одного и того же тела, например между слоями жидкости или газа.

8.4.Сила трения скольжения Fтр пропорциональна силе нормального давления N, с которой одно тело действует на другое (закон Кулона-Амонтона)

Fтр = fтр N

где fтр – коэффициент трения скольжения.

8.5.Сила трения качения пропорциональна силе нормального давления N, с которой одно тело действует на другое, и обратно пропорциональна радиусу r катящегося тела

(закон Кулона)

Fтр = fк Nr

где fк – коэффициент трения качения.

9. Уравнение поступательного движения тела переменной массы (уравнение Мещерского) m ddtv = Fвнеш +(v1 −v)dmdt

где m и v – масса и скорость тела в рассматриваемый момент времени, Fвнеш - главный вектор внешних сил, v1 – скорость отделяющихся частиц после отделения (если dmdt < 0 ),

либо присоединяющихся частиц до присоединения (если dmdt > 0 ).

9.1. Второе слагаемое в правой части уравнения Мещерского

(v1 −v)dmdt = u dmdt = Fp

называется реактивной силой

9.2. В отсутствие внешних сил

m ddtv = u dmdt

9.3.Если начальная скорость тела равна нулю, то тело движется прямолинейно в направлении, противоположном относительной скорости u отделяющихся частиц

m dvdt = −u dmdt

и при u = const

где m0 - начальная масса тела.

Лекция 3

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Основной закон динамики вращательного движения абсолютно твердого тела. Момент силы, момент инерции. Расчет момента инерции тел простой формы. Теорема Штейнера. Момент импульса, закон сохранения момента импульса.

1.Моментом инерции механической системы относительно неподвижной оси а называ-

ется физическая величина Ja, равная сумме произведений масс m всех n материаль-

ных точек системы на квадраты их расстояний r до оси

n

Ja = ∑mi ri2

i=1

1.1. Момент инерции неоднородного тела

Ja = ∫r2dm = ∫r2 DdV

m V

где dm = DdV – масса элементарного объема тела dV , D – плотность. 1.2. Момент инерции однородного тела

J a = D∫r 2 dV

V

1.3.Момент инерции тела J относительно произвольной оси равен сумме момента

инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d

между осями (теорема Гюйгенса-Штейнера)

J= Jc +md2

1.4.Моменты инерции тел простой формы

1.5.Центробежными моментами инерции тела по отношению к осям декартовой сис-

темы координат называются величины

J xy = ∫xydm = ∫xyDdV

m V

J xz = ∫xzdm = ∫xzDdV

m V

J yz = ∫yzdm = ∫yzDdV

m V

2

1.5.1.Главной осью инерции тела называется ось ОХ, положение которой в про-

странстве выбрано таким образом, что центробежные моменты Jxz и Jyz одновременно равны нулю.

1.5.2.Через каждую точку тела можно провести три главные оси инерции, которые перпендикулярны друг другу.

1.5.3.Главными моментами инерции тела называются моменты инерции относительно главных осей инерции, проведенных в произвольной точке тела.

1.5.4.Если главные оси инерции проходят через центр масс тела, то такие оси назы-

ваются главными центральными осями инерции тела, а моменты инерции относительно этих осей называются главными центральными моментами инерции тела.

2.Моментом импульса (моментом количества движения) материальной точки отно-

сительно неподвижной точки О называется вектор L, равный векторному произведению

радиус-вектора r, проведенного из точки О в место нахождения материальной точки, на вектор p ее импульса

L= [rGpG]= [rGmvG]

2.1.Момент импульса системы относительно неподвижной точки

LG = ∑n [rGi pGi ]= ∑n [rGi mivGi ] i=1 i=1

2.2.Момент импульса системы относительно неподвижной оси а – проекция на эту ось вектора L момента импульса системы, относительно какой-либо точки, лежащей на этой оси

2.3. Если тело вращается с угловой скоростью ω вокруг точки О, то момент импульса те-

mm

ив общем случае направления векторов L и ω не совпадают.

2.4.Если тело вращается вокруг одной из главных осей инерции, то направление вектора момента импульса тела совпадает с направлением вектора его угловой скорости, а значение момента импульса может быть выражено через момент инерции

L = JωG

3.Моментом силы F относительно неподвижной точки О называ-

ется векторная величина М, равная векторному произведению радиус-вектора r, проведенного из точки О в точку А приложе-

ния силы, на вектор силы F (правило рычага)

M = [rGF ]

3.1. Модуль момента силы

M = Fr sinα = Fl

где l – длина перпендикуляра, опущенного из точки О на линию действия силы.

3.2.Главным моментом силы (результирующим моментом) нескольких сил относительно неподвижной точки О (полюса) называется вектор М, равный геометрической сумме моментов относительно точки О всех действующих сил

MG = ∑n [rGi FGi ]

i=1

3

3.3.Моментом силы F относительно неподвижной а называется величина Ма, равная проекции на эту ось вектора М момента силы F относительно произвольной точки О на оси а

M a = M aia

3.4.Если линия действия силы пересекает ось или параллельна ей, то момент силы относительно этой оси равен нулю.

3.5.Первая производная по времени t от момента импульса L механической системы

относительно любой неподвижной точки О равна главному моменту Мвнешн отно-

сительно той же точки О всех внешних сил, приложенных к системе (основной закон динамики твердого тела, вращающегося вокруг неподвижной точки)

ddtL = Mвнешн

3.6.Основной закон динамики твердого тела, вращающегося вокруг неподвижной оси

OZ

где ε = dω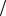dt – угловое ускорение тела.

4.Момент импульса замкнутой системы относительно любой неподвижной точки не изменяется с течением времени (закон сохранения момента импульса)

ddtL ≡ 0 и L = const

5.Движение свободного твердого тела удовлетворяет следующим двум дифференциальным уравнениям

dtd (mvc ) = Fвнешн

dtd Lc = Mвнешн

первое из которых описывает поступательное движение свободного тела со скоростью его центра масс, а второе описывает вращение твердого тела вокруг его центра масс.