

1
5.2.7. Декодеры групповых систематических кодов. Оценка сложности аппаратной реализации
Обобщенная функциональная схема декодера ГСК приведена на рис. 5.6. Обозначения на данном рисунке, совпадающие с аналогичными обозначениями на рис. 5.3, дополнительно не поясняются.
Рис. 5.6. Обобщенная функциональная схема декодера ГСК
На входы декодера параллельно либо последовательно во времени поступают неискаженные или искаженные кодовые векторы ГСК. В системах передачи информации (системах связи) используются последовательные сигналы на входе декодера, а в системах хранения информации − параллельные сигналы на входе декодера.
Декодер ГСК так же, как и кодер ГСК, в общем случае представляет собой (a, b)-многополюсник. В зависимости от способа представления во времени входного и выходного сигналов декодера и режимов использования входного (БРn) и выходного (МБРn) регистров декодера возможны следующие варианты значений а и b: (1, 1), (n, 1), (1, n), (n, n). Пояснения приводимых вариантов декодеров ГСК аналогичны тем пояснениям, которые давались выше для кодеров ГСК.
В составе декодера выделим: входной буферный регистр (БРn); корректор, который состоит из устройства вычисления синдрома (УВС) и декомбинатора синдрома (ДКМС) и реализует однозначное соответствие между значением синдрома и вектором ошибки; выходной многорежимный буферный регистр (МБРn).
2
Возможны разные варианты реализации корректора, некоторые из них будут рассмотрены ниже.
Скорректированная информация хранится в многорежимном буферном регистре (МБРn) декодера. МБРn состоит из многофункциональных триггеров с установочным и счетным входами, что позволяет реализовать процедуру записи в МБРn исходного вектора и коррекции ошибок. Через ε обозначен выход ДКМС (корректора), равный единице при обнаружении ошибок и обеспечивающий стирание полученного сообщения. Информация с выхода МБРn может считываться последовательно либо параллельно во времени, что обусловлено режимом использования МБРn.
Выделим две реализации УВС – параллельного и последовательного типа в зависимости от представления во времени сигнала на входе УВС.
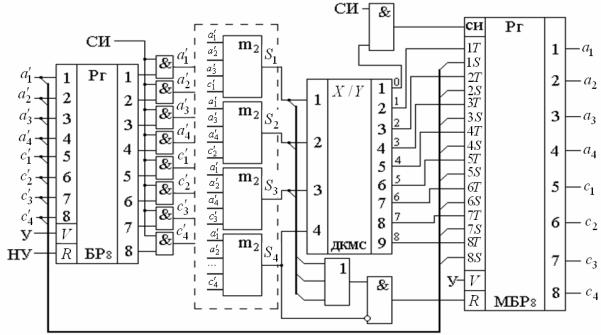
Пример 5.12. Рассмотрим развернутые функциональные схемы декодеров ГСК с УВС параллельного и последовательного типа, реализующих уравнения (5.15) для ГСК (8,4,4) из примера 5.10. На рис. 5.7 показана развернутая функциональная схема декодера с УВС параллельного типа, реализованы в базисе сумматоров по модулю два, а на рис. 5.8 − развернутая функциональная схема декодера ГСК (8,4,4) с УВС последовательного типа. В данном случае УВС состоит из комбинатора синдрома (КМС) и буферного регистра синдрома с k триггерами со счетным входом, каждый из которых реализует суммирование по модулю для определенных групп символов (согласно (5.15)), поступающих последовательно во времени на вход КМС.
Рис. 5.7. Развернутая функциональная схема декодера ГСК (8, 4, 4) с УВС параллельного типа

3
Рис. 5.8. Развернутая функциональная схема декодера ГСК (8, 4, 4)
сУВС последовательного типа
Всоответствии с обобщенной функциональной схемой декодера ГСК, представленной на рис. 5.6, может быть предложена следующая верхняя оценка сложности аппаратной реализации через число элементов памяти и комбинационных элементов:
Nэл = 2nэп + n& + n kmod 2 + mэп + 2&k, |
(5.18) |
где 2nэп – число элементов памяти в БРn и МБРn; mэп – число элементов памяти в БРС; n kmod 2 – верхняя оценка числа двухвходовых сумматоров по модулю два или дизъюнкторов в составе УВС; 2&k – верхняя оценка числа k-входовых конъюнкторов в ДКМС; в том случае, если вместо ДКМС используется ПЗУ векторов ошибок, то сложность ПЗУ равна 2k n элементов памяти; n& – число двухвходовых конъюнкторов на выходе БРn.
Как видно из приведенной оценки (5.18), основным недостатком синдромных декодеров ГСК является показательный рост сложности декомбинаторов синдрома при аппаратной реализации или ПЗУ ошибок при аппаратно-программной реализации. Для преодоления этого недостатка были предложены другие виды линейных алгебраических кодов (циклические, коды с подстановками, каскадные и т.д.) и алгебраические методы (алгоритмы) декодирования [9,10,12,13,14], не рассматриваемые в настоящем разделе.
