
1
3. ОБЩИЕ ПРИНЦИПЫ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК ИЗБЫТОЧНЫМИ КОДАМИ
3.1. Мера избыточности кода
Введем ряд обозначений: М0 – полное множество всех возможных комбинаций кода с мощностью кодового алфавита, равной α (в главе 1 применялся символ k), и длиной кодовых слов, равной n,
M0 = αn , |
(3.1) |
где Mр – множество рабочих комбинаций кода (комбинаций, используемых для кодирования сообщений),
Mр = αm , |
(3.2) |
где m = [log Mр]; [x] – ближайшее целое, большее х; m – число информационных символов кода. Тогда (n – m) определяет число избыточных символов k, а (М0 – Мр) – число запрещенных комбинаций кода Мз.
Введем две меры избыточности кода RI и RII (0 ≤ RI, RII ≤ 1):
R = |
M0 −Mр |
= |
M з |
, |
(3.3) |
|||
|
|
|
||||||
I |
M0 |
|
M0 |
|
||||
|
|
|
|
|||||
|
R |
= |
n −m |
= k . |
(3.4) |
|||
|
|
|||||||
|
II |
|
n |
|
n |
|
||
|
|
|
|
|
||||
RI – оценка избыточности как доли запрещенных (не используемых для кодирования сообщений) кодовых комбинаций среди всех возможных. Она является точной оценкой избыточности кода, но, к сожалению, редко используется, т. к. n >> 1 и m >> 1 и соответствующие им степени (М0 и Мр) – слишком большие числа.
RII – оценка избыточности как доли разницы между длиной кодовой комбинации n и количеством символов, которые бы понадобились для неизбыточного кодирования Мр сообщений. Она является грубой оценкой избыточности кода, получившая наибольшее практическое применение, т.к. легче иметь дело с показателями степеней, чем с самими степенями.
Величина, обратная RII, для двоичных кодов (α = 2) часто называется скоростью передачи информации (информационной содержательностью)
Rи и измеряется в единицах [бит/символ],
Rи = 1 – RII = m / n log2 α = m / n.
2
3.2. Оценка помехоустойчивости при передаче дискретных сообщений
Введем ряд понятий и обозначений, исследуемых в дальнейшем. Обозначим двоичный n-разрядный кодовый вектор (кодовую комбинацию) через
V =(a1, a2 ,..., ai ,..., an ),ai =0,1.
Обозначим n-разрядный вектор ошибки через
e = (e1, e2 ,..., ei ,..., en ),ei = 0,1.
Ошибка (искажение) в i-м разряде кодового вектора означает подмену одного (передаваемого) кодового символа другим, не равным ему. При этом в i-м разряде вектора ошибки появляется единица.
Обозначим вектор на выходе канала передачи данных (КПД) через V ' =(a1′, a2′,..., ai′,..., an′ ),ai′ =0,1. Примем аддитивную модель взаимодейст-
вия передаваемого вектора V и вектора ошибок (шума), т. е. |
|
V ′=V e . |
(3.5) |
Тогда для двоичного канала ошибка при передаче i-го символа означает его инвертирование. Инверсия двоичного символа эквивалентна выполнению логической операции «исключающее или» («суммирование по модулю два») с логическим символом «1»: ai′ = ai 1.
Введем метрику рассматриваемого кодового пространства. Норма (величина) кодового вектора равна его весу:

 V
V 
 = w(V ),
= w(V ),
где w(V ) – вес кодового вектора, т. е. число его ненулевых компонентов (разрядов).
Тогда расстояние между двумя кодовыми векторами V1 и V2
d(V1,V2 ) = 
 V1 −V2
V1 −V2 

и равно весу разности этих векторов по mod α , т. е.
|
|
|
|
|
|
|
|
|
|
d(V1 |
,V2 ) = w(V1 −V2 )mod α. |
(3.6) |
|||||||

3
При α = 2
|
|
|
|
|
|
|
|
|
|
d(V1 |
,V2 ) = w(V1 V2 ) . |
(3.7) |
|||||||
Введенное кодовое расстояние, называемое расстоянием Хемминга,
равно числу разрядов, в которых различаются два сравниваемых вектора
V1 и V2 .
Пример 3.1. Пусть V1 =1010 и V2 =1110 , тогда w(V1) =2; w(V2 ) =3; d(V1,V2 ) = w(V1 V2 ) = w(1010 1110) = w(0100) =1, т. е. два сравниваемых
вектора различаются только во втором разряде.
Пример 3.2. Пусть V1 = 1010 и e = 0010, тогда V1′=1010 0010 =
= 1000. Следовательно, ошибка произошла в третьем разряде передаваемого вектора, т. к. именно этот разряд вектора ошибки равен 1.
Из (3.5) следует, что
e =V ′ V .
Назовем вес вектора ошибки кратностью ошибки. Так, в примере 3.2 w(e) = 1, т. к. имеет место однократная ошибка. Проанализируем события, имеющие место при передаче информации по двоичному симметричному каналу n-разрядным двоичным неизбыточным кодом, для которого справедливо равенство
М0 = М = 2n,
и, следовательно,
RI = RII = 0.
Рассмотрим вероятностные соотношения для передачи сообщений кодовыми комбинациями.
Событие, при котором вся кодовая комбинация принимается правильно, возникает в случае правильного приема всех символов кодовой комбинации. Для симметричного двоичного канала вероятность правильного приема сообщения (отсутствия ошибок) P(0) определяется следующим образом:
P(0) = qn = (1 − p)n , |
(3.8) |
где n – длина кодовой комбинации; q – вероятность правильной передачи символа; p – вероятность неправильного (ошибочного) приема одного символа (вероятность ошибки на символ).
4
Обобщим приведенные соображения, записав вероятность полной группы событий, возникающих при приеме кодовой комбинации. Действительно, возможно одно из следующих событий: нет ошибок – с вероятностью P(0), однократная ошибка в любом разряде – с вероятностью P(1), двукратная ошибка в любых разрядах – с вероятностью P(2), и т. д. Сумма вероятностей, образующих полную группу независимых событий, равна 1:
n |
n |
n |
pi (1 − p)n−i =1. |
(3.9) |
∑P(i) = ∑ |
|
|||
i =0 |
i =0 |
i |
|
|
Рассмотрим, какие могут возникать события после приема кодовых комбинаций кодом неизбыточного кода, т.е. без дополнительных возможностей по повышению достоверности и помехоустойчивости передачи сообщений. Таких событий возможно два:
•правильная передача сообщения – имеет место при правильном приеме всех символов;
•трансформация сообщения – возникает при появлении ошибок, поскольку вместо переданной кодовой комбинации (сообщения) получателю информации будет выдана другая кодовая комбинация (сообщение).
Поскольку указанные варианты образуют полную группу событий,
то сумма их вероятностей равна 1. Вероятность правильной передачи Pпр определяется вероятностью P(0), а вероятность трансформации Pтр – суммой всех остальных вероятностей от P(1) до P(n):
Pпр + Pтр =1,
Pпр = P(0) = (1 −
n
Pтр =1 − Pпр = ∑ i=1
p)n , |
|
(3.10) |
n |
n |
pi (1 − p)n−i . |
P(i) = ∑ |
|
|
i=1 |
i |
|
Для наглядности анализа указанных событий воспользуемся графом канала передачи данных (ГКПД). При этом на входе дуги находится кодовая комбинация из множества рабочих комбинаций кода { Ai }, а на выходе дуги – кодовая комбинация, наблюдаемая на выходе канала. Это могут быть либо кодовое слово из { Ai } при правильной передаче или трансформации сообщения, либо кодовое слово из множества запрещенных комбинаций кода { Bi } при искаженной передаче. Ребро ГКПД нагружено соот-
ветствующим значением вектора ошибки.
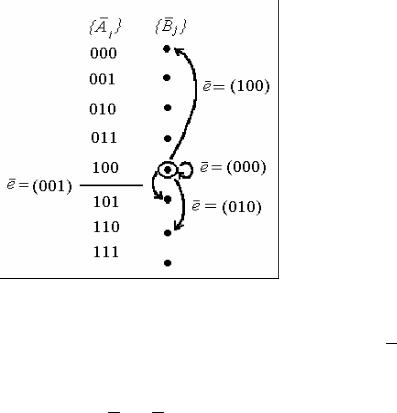
Пример 3.3. Пусть М0 = М = 23. ГКПД показан на рис. 3.1.
5
Рис. 3.1. ГКПД при передаче сообщений неизбыточным кодом n = 3
Из рис. 3.1 видно, что т. к. М0 – М = 0, то подмножество { Bi } – пус-
тое, и, следовательно, любая ошибка вызывает трансформацию сообщения, т.е. является необнаруженной. Действительно, если передается кодовый вектор (кодовая комбинация) A4 = V4 = 100, то искажение (ошибка) в лю-
бом разряде вызывает переход в одну из разрешенных комбинаций и получателю выдается другое сообщение.
Таким образом, неизбыточный код не способен обнаруживать ошибки никакой кратности. Возможность кода обеспечить (повысить) достоверность и помехоустойчивость передачи сообщений сводится к наличию у него корректирующих свойств. Они заключаются в том, что даже при наличии некоторого количества ошибок в принятом сообщении трансформации сообщения не возникнет.
Корректирующие свойства кода могут быть направлены на два вида действий:
•исправление ошибок;
•обнаружение ошибок.
Исправление сводится к обнаружению факта наличия ошибок, к определению мест их возникновения (ошибочных разрядов), замене ошибочных символов правильными. Обнаружение сводится только к обнаружению факта наличия ошибок в кодовой комбинации. При этом для недопущения трансформации сообщение с ошибками нужно стереть, а получателя – проинформировать об этом.
Разумеется, процесс исправления ошибок требует более сложного алгоритма обработки и дополнительных затрат, зато более эффективен. Процесс обнаружения ошибок менее требователен к затрачиваемым ресурсам, но и менее эффективен, поскольку требует дополнительных повто-
6
ров, запросов, подтверждений и т. п. Поэтому он применяется только в системах с обратной связью.
Корректирующие свойства кода могут быть направлены на обнаружение и/или исправление ошибок. Рассмотрим далее общие принципы обнаружения и исправления ошибок корректирующими кодами.
