

1
3.3. Обнаружение ошибок избыточными кодами
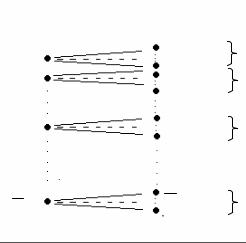
Рассмотрим структуру избыточного кода (рис. 3.2), обнаруживающего ошибки. В нем выделяются два множества: { Ai } и { Bi }.
|
|
|
|
{ |
|
|
{ |
|
j } |
|
|
|
|
|
|
|
|
|
Ai } |
|
|
|
|
||||||
|
|
|
|
B |
|
|
|
|
||||||
|
|
|
|
• |
• |
|
|
|
|
|||||
A1 |
||||||||||||||
|
B |
|||||||||||||
. |
|
|
• |
• |
1 |
|||||||||
|
|
. |
|
|
||||||||||
. |
|
|
|
|
|
|
|
|
. |
|
|
|||
. |
|
|
• |
• |
. |
|
|
|||||||
|
|
|
|
|
j |
|||||||||
Ai |
||||||||||||||
|
B |
|||||||||||||
. |
|
|
|
|
|
|
|
|
. |
|
|
|||
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
. |
|
|
||||
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
• |
• |
. |
|
|
||||||||
|
|
|
|
|
|
|||||||||
AM |
||||||||||||||
р |
|
|
|
|
B |
|
||||||||
|
|
|
|
|
|
|
|
M з |
||||||
Рис. 3.2. ГКПД при передаче сообщений избыточным кодом, обнаруживающим ошибки
Согласно (3.3) избыточность построенного кода RI = M 0 − M .
M 0
Покажем, что благодаря введенной избыточности данный код обнаруживает ошибки. Проиллюстрируем с помощью ГКПД передачу сообщений кодом, обнаруживающим ошибки, по ДСК.
|
|
{ |
|
|
{ |
B |
j } |
||
|
|
Ai } |
|||||||
|
A1 |
|
|
|
|
|
|||
|
|
|
B |
||||||
|
|
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
||||
|
|
|
|
|
|
B j |
|||
|
i |
|
|
||||||
A |
M р |
|
|
B |
|||
|
|
M з |
|
Рис. 3.3. ГКПД при передаче сообщений избыточным кодом, обнаруживающим ошибки
Из рис. 3.3 видно, что при передаче сообщений кодом, обнаруживающим ошибки, имеют место три события: правильная передача (неискаженная), трансформация сообщения, вызываемая необнаруженной ошибкой, и стирание сообщения, вызываемое обнаруженной ошибкой. Обнаружение ошибки происходит при появлении на выходе ДСК (на входе
2
декодера) запрещеной комбинации. Доля обнаруживаемых ошибок равна
M0 −M р , т. е. совпадает с избыточностью кода.
M0
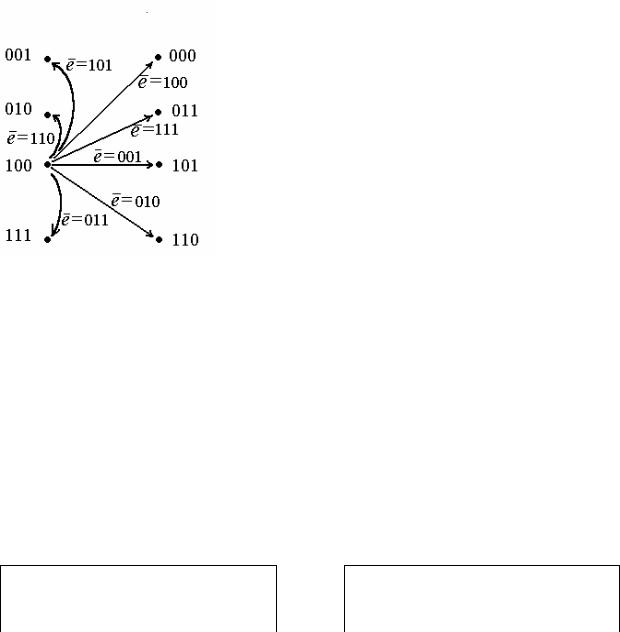
Пример 3.4. Представим неизбыточный код из примера 3.3 с помощью разбиения рис. 3.2, получив в итоге избыточный код, представленный на рис. 3.4. На этом же рисунке проиллюстрирован и процесс передачи информации.
{ |
Ai } |
{ |
B |
j } |
|
|
|
|
|
Рис. 3.4. ГКПД при передаче сообщений избыточным кодом n = 3, обнаруживающим ошибки нечетной кратности
Разобьем полное множество комбинаций на два непересекающихся множества: множество рабочих комбинаций Мр и множество запрещенных комбинаций Мз. Для первичного кодирования будем использовать только рабочие комбинации Ai.
Мр
A1 |
A2 |
A3 |
A4 |
001 |
010 |
100 |
111 |
Мз
B1 |
B2 |
B3 |
B4 |
000 |
011 |
101 |
110 |
Размерность каждого из множеств равна 4, следовательно,
M 0 = M р + Мз = 4 + 4 =8.
Проверим корректирующие свойства построенного кода, состоящего из рабочих комбинаци Ai, на примере однократных искажений для любой кодовой комбинации, например A3.
3
A3 100 →e1 000 B1 Мз,
A3 100 →e2 110 B4 Мз,
A3 100 →e3 101B3 Мз.
Из приведенного анализа очевидно, что любые однократные искажения переводят комбинацию из множества Мр в множество Мз. Таким образом, ошибка может быть обнаружена путем проверки на принадлежность принятой кодовой комбинации одному из множеств. Для рассматриваемого кода можно оценить корректирующие свойства как способность обнаруживать любые однократные и трехкратные ошибки. Нетрудно убедиться, что двукратные ошибки не могут быть обнаружены, поскольку они оставляют принятую кодовую комбинацию во множестве Мр.
Для исправления ошибки характеристик кода недостаточно. Действительно, любую из комбинаций Bj можно получить в результате ошибки одинаковой кратности в разных рабочих кодовых комбинациях. Например, комбинацию B1 можно получить в результате однократной ошибки e1 в A3,
e2 в A2 или e3 в A1.
Кодовые комбинации, принадлежащие множеству запрещенных комбинаций, называют избыточными, поскольку они не используются для первичного кодирования сообщений. Однако, как мы убедились на приме-
ре, присутствие избыточных комбинаций в полном множестве кодо-
вых комбинаций является необходимым условием построения кода, корректирующего ошибки.
Избыточность построенного кода оценивается, как RI = 0,5; RII = 0,33. Минимальное кодовое расстояние dmin = 2. Код обнаруживает любые ошибки нечетной кратности. Ошибки четной кратности не обнаруживаются, т.е. вызывают трансформацию сообщений. Можно ввести параметр r как кратность обнаруживаемых ошибок, т.е. код гарантирует обнаружение ошибок кратности не более r.
Рассмотрим вероятностные соотношения при реализации корректирующих свойств кода, направленных на обнаружение ошибок.
Сообщение будет принято правильно, если ошибок в кодовой комбинации нет (вероятность этого события Pпр). Все ошибки кратности не более r будут обнаружены, и сообщение будет стерто (вероятность этого события Pст). Если кратность ошибок превысит r, то произойдет трансформация сообщения (вероятность этого события Pтр).
Запишем сформулированные условия:
w(e) = 0 − |
– правильная передача сообщения, |
|
|
|
|
0 |
< w(e) ≤ r– стирание сообщения, |
|
|
w(e) > r – трансформация сообщения. |
|
|
||
4
Вероятностные соотношения выглядят следующим образом:
Pпр + Pст + Pтр =1, |
|
|
|
|||
P |
= P(0) = |
(1 − p)n , |
|
|
|
|
пр |
|
|
|
|
|
|
Pст |
r |
r |
n |
pi (1 |
− p)n−i , |
(3.11) |
= ∑P(i) |
= ∑ |
|
||||
|
i=1 |
i=1 |
i |
|
|
|
n |
n |
n |
pi (1 − p)n−i . |
Pтр =1 − Pпр − Pст = ∑P(i) = |
∑ |
|
|
i=r +1 |
i=r+1 |
i |
|
Как видно из приведенных соотношений, вероятность трансформации уменьшается из-за появления вероятности стирания.
Очевидно, что для кода, не имеющего корректирующих свойств, избыточность равна 0. Поэтому корректирующие коды еще называют избы-
точными. Очевидно, что чем больше избыточность, тем выше коррек-
тирующие свойства кода. Покажем это, построив код, исправляющий ошибки.
3.4. Исправление ошибок избыточными кодами
Общая структура кода, исправляющего ошибки, представлена на рис. 3.5.
{ |
|
} |
{ |
|
|
|
|
|
|
||
A |
Bi } |
|
|||||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L1 |
||
|
|
|
|
|
B1 |
||||||
A |
|
|
|
||||||||
1 |
|
|
|
|
|
|
|
|
L2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|||
Ai |
|
|
|
|
|
Li |
|||||
|
|
|
i |
||||||||
A |
BM з |
LM |
р |
M р |
|
|
Рис. 3.5. Структура кода, исправляющего ошибки
Для построения кода, исправляющего ошибки, необходимо полное множество М0 комбинаций кода разбить на М непересекающихся подмножеств так, что

5
M р |
|
M0 = ∑(Li +1) , |
(3.12) |
i=1 |
|
где Li – мощность i-го подмножества запрещенных комбинаций; Li + 1 – мощность подмножества, включая i-ю рабочую комбинацию; данное подмножество называют сигнальной зоной (сферой) i-й рабочей комбинации.
n |
, где S – кратность ис- |
|
Мощность Li может быть определена как |
|
|
|
|
|
S |
|
|
правляемых ошибок.
Таким образом, разбиение типа рис. 3.5 удовлетворяет следующим условиям:
Lν ∩ Lµ =Ø ,
M |
−M р. |
|
∑Li ≤ M0 |
(3.13) |
|
i=1 |
|
|
Способ приема состоит в том, что если принята некоторая комбинация из i-го подмножества, то декодером выносится решение о том, что передана комбинация Ai . Таким образом, исправляется та часть всевозмож-
ных ошибок, под действием которых i-я рабочая комбинация ( Ai ) не выхо-
дит за пределы i-й сигнальной зоны. При этом знак равенства в (3.13) означает, что построен код, исправляющий ошибки, так называемый «плотноупакованный»; знак < означает, что корректирующая способность кода использована либо для исправления ошибок, либо для исправления и обнаружения ошибок. Доля исправляемых ошибок, в предположении, что все
M р |
1 |
|
|
L |
|
1 |
|
|
рабочие комбинации равновероятны, составляет ∑ |
|
|
|
i |
= |
|
|
. |
|
|
M0 −M р |
M |
|
||||
i=1 M |
р |
|
р |
|||||
Корректирующая способность избыточного кода должна быть использована для исправления наиболее вероятных ошибок в канале связи. Выполнение этого требования обусловлено конструированием сигнальных зон. Для ДСК, т. е. двоичных симметричных каналов связи, описываемых биномиальным законом распределения ошибок, справедливо соотношение
P(i) > P (i + 1), |
(3.14) |
т.е. ошибки малой кратности более вероятны, чем ошибки большой кратности. Поэтому в i-ю сигнальную зону включаются запрещенные комбинации Bi , удаленные от Ai на наименьшее кодовое расстояние по сравне-
нию с удаленностью от любой другой рабочей комбинации. Тогда оптимальное декодирование исправляющего ошибки кода, учитывающее статистику ошибок в канале связи, будет заключаться в вычислении кодового

6
расстояния от принятого кодового вектора до всех { Ai } (i =1, M) и выне-
сении решения в пользу той рабочей комбинации, до которой кодовое расстояние минимально. Подобная схема принятия решения называется деко-
дированием по критерию максимального правдоподобия, которое считает-
ся оптимальным.
Пример 3.5. Построим код, исправляющий однократные ошибки согласно схеме разбиений рис. 3.5.
На рис. 3.6. приведен код с d( A1, A2 ) = 3, исправляющий все возмож-
ные однократные ошибки, и ГКПД, иллюстрирующий процесс передачи информации указанным кодом. Построенный код является плотноупакованным. В КПД имеют место 2 события: правильная передача сообщений и трансформация. Правильная передача имеет место как при отсутствии ошибок, так и при любой однократной ошибке. Из рис. 3.6 видно, что построенный код исправляет любую однократную ошибку, т.к. запрещенная комбинация не выходит из сигнальной зоны соответствующей рабочей комбинации, искаженной однократной ошибкой попутно. Отметим, что сигнальные зоны кода, обнаруживающего ошибки, состоят только из рабо-
чих комбинаций кода, т. е. Li = L = 1, (i =1, M) .
|
|
|
|
|
001 |
– |
|
|
|
|
|||
|
|
|
|
e =100 |
B1 |
||||||||
|
|
|
|
e = 010 |
|
|
|
|
|
|
|||
A1 |
|
|
|
|
|
|
|||||||
111 |
– B2 |
||||||||||||
101 |
|
|
|
||||||||||
e = 001 |
100 |
– |
|
|
|
||||||||
|
|
|
|
B3 |
|||||||||
|
|
|
|
e = 100 |
|
|
|
|
|
|
|||
|
|
|
|
110 |
– B4 |
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
e= 010 |
|
|
|
|
|
|
||
A2 |
|
000 |
– |
|
|
|
|||||||
|
|
|
B5 |
||||||||||
101 |
e = 001 |
|
|
|
|
|
|
||||||
|
|
|
|
011 |
– B6 |
||||||||
|
|
|
|
|
|
|
|||||||
Рис. 3.6. Структура избыточного кода n = 3, исправляющего однократные ошибки и ГКПД
Оценим избыточность кода, исправляющего однократную ошибку.
|
RI = |
|
M 0 |
−M р |
|
= |
|
8 − |
2 |
= |
3 |
, |
|
|
|
|
|||
|
|
|
M 0 |
8 |
|
|
4 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
RII = |
n −m |
= |
n −[log2 |
M р |
] |
= |
3 −1 |
= |
2 |
. |
|||||||||
n |
|
n |
|
|
|
|
|
3 |
|
3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
7
Минимальное кодовое расстояние dmin = 3.
Еще раз отметим, что чем больше избыточность, тем сильнее корректирующие свойства кода.
Сигнальная зона содержит и кодовые комбинации, которые отличаются от данной рабочей комбинации не более чем в S разрядах, а от остальных рабочих комбинаций – более чем в S разрядах. Поэтому ошибка кратности не более чем S приведет в сигнальную зону переданной рабочей комбинации, что дает возможность для исправления ошибки. При этом ошибки кратности более чем S приведут либо в сигнальную зону другой рабочей комбинации, либо непосредственно в другую рабочую комбинацию, что вызовет трансформацию сообщения. Поэтому можно ввести параметр S как кратность исправляемых ошибок.
Рассмотрим вероятностные соотношения при реализации корректирующих свойств кода, направленных на исправление ошибок.
Будем считать, что все ошибки кратности не более S будут исправлены и сообщение будет принято правильно (вероятность этого события Pпр). Если кратность ошибок превысит S, то произойдет трансформация сообщения (вероятность этого события Pтр). Запишем сформулированные условия:
0 ≤ w(e) ≤ S |
– правильная передача сообщения, |
|
|
w(e) > S |
– трансформация сообщения. |
|
||
Вероятностные соотношения выглядят следующим образом:
Pпр + Pтр =1, |
|
|
|
|
S |
S |
n |
pi (1 − p)n−i , |
(3.15) |
Pпр = ∑P(i) |
= ∑ |
|
||
i=0 |
i=0 |
i |
|
|
n |
n |
n |
pi (1 − p)n−i . |
Pтр =1 − Pпр = ∑P(i) = |
∑ |
|
|
i=S +1 |
i=S +1 |
i |
|
Как видно из приведенных соотношений, вероятность трансформации уменьшается из-за увеличения вероятности правильной передачи.
3.5. Исправление и обнаружение ошибок избыточными кодами
Рассмотрим избыточные коды, у которых корректирующие свойства направлены на обнаружение и исправление ошибок. Очевидно, что полное множество запрещенных комбинаций содержит подмножество сигнальных

8
зон, предназначенное для исправления ошибок, и подмножество запрещенных комбинаций, предназначенное для обнаружения ошибок. При этом кодовое расстояние до подмножества запрещенных комбинаций больше, чем ширина сигнальной зоны. Это означает, что параметр r для рассматриваемого вида корректирующих кодов всегда больше S.
Пример 3.6. Построим код длины n = 4, исправляющий однократные и обнаруживающий двукратные ошибки.
На рис. 3.7. приведен код с d( A1, A2 ) = 4, исправляющий все одно-
кратные и обнаруживающий все двукратные ошибки, и ГКПД, иллюстрирующий процесс передачи информации указанным кодом. Построенный код является плотноупакованным. В КПД имеют место 3 события: правильная передача сообщений, стирание и трансформация. Правильная передача имеет место как при их отсутствии ошибок, так и при любой однократной ошибке. Стирание происходит при двукратной ошибке. Из рис. 3.7 видно, что построенный код исправляет любую однократную ошибку, т. к. запрещенная комбинация не выходит из сигнальной зоны соответствующей рабочей комбинации, искаженной однократной ошибкой попутно. Двукратные ошибки также будут обнаружены, поскольку переведут рабочую комбинацию во множество запрещенных состояний Мз.
|
|
w(e) = 1 |
• 1101 : |
B11 |
|
|
||
|
|
• 0001 : |
|
|
1 |
|
Мз |
|
|
|
B |
|
|||||
A1 : 0101 • |
2 |
|
• 0110 |
|||||
• 0111 : |
B31 |
|
||||||
|
|
|
• 0100 : |
|
|
41 |
|
• 0011 |
|
|
|
B |
w(e) = 2 |
||||
|
|
|
|
|
|
|
• 1001 |
|
|
|
|
|
|
|
|
w(e) = 2 |
• 0000 |
|
|
|
• 0010 : |
B12 |
• 1111 |
|||
|
|
|
|
|||||
|
|
: 1010 • |
• 1110 : |
B22 |
|
• 1100 |
||
A2 |
|
|||||||
• 1000 : |
|
2 |
|
|
||||
B |
|
|
||||||
|
|
w(e) = 1 |
3 |
|
|
|||
|
|
|
• 1011 : |
|
2 |
|
|
|
|
|
|
B |
|
|
|||
|
|
|
4 |
|
|
|||
Рис. 3.7. Структура избыточного кода n = 4, исправляющего однократные и обнаруживающиего двукратные ошибки и ГКПД
Оценим избыточность кода, исправляющего однократную и обнаруживающего двукратную ошибки.
RI = M0 −M р =16 −2 = 7 ,
M0 16 8
9
R = n −m |
= |
n −[log2 Mр] |
= 4 −1 = 3 . |
|
|
||||
II |
n |
|
n |
4 4 |
|
|
|||
Минимальное кодовое расстояние dmin = 4.
Рассмотрим вероятностные соотношения при реализации корректирующих свойств кода, направленных на исправление и обнаружение ошибок.
Будем сичтать, что сообщение будет принято правильно, если ошибок в кодовой комбинации нет или кратность ошибок не превышает S, и они будут исправлены (вероятность этого события Pпр). Все ошибки кратности более S и менее r будут обнаружены, и сообщение будет стерто (вероятность этого события Pст). Если кратность ошибок превысит r, то произойдет трансформация сообщения (вероятность этого события Pтр).
Запишем сформулированные условия:
0 ≤ w(e) ≤ S – правильная передача сообщения, |
||
|
|
|
S < w(e) ≤ r – стирание сообщения, |
||
|
w(e) > r |
– трансформация сообщения. |
|
||
Вероятностные соотношения выглядят следующим образом:
Pпр + Pст + Pтр |
=1, |
|
|
|
||
S |
|
S |
n |
pi (1 − p)n−i , |
||
Pпр = ∑P(i) |
= ∑ |
|
|
|||
i=0 |
|
i=0 |
i |
|
|
|
r |
|
|
r |
n |
(3.16) |
|
Pст = ∑P(i) = ∑ |
|
|
pi (1 − p)n−i , |
|||
i=S +1 |
|
i=S +1 |
i |
|
||
n |
n |
n |
pi (1 − p)n−i . |
Pтр =1 − Pпр − Pст = ∑P(i) = |
∑ |
|
|
i=r +1 |
i=r+1 |
i |
|
Как видно из приведенных соотношений, вероятность трансформации уменьшается из-за исправления ошибок (увеличения вероятности правильной передачи) и появления вероятности стирания (обнаружения ошибок).
