TKz-12_Obschaya_teoria_svyazi_chast_2 / 03

1

2.2. Математические модели дискретных каналов с памятью

Введем ряд понятий (сущностей), определений и обозначений.

Множество состояний канала с памятью (КСП) – характеризует конечное множество состояний, в которых может находиться КСП. Обозначим через R – мощность этого множества. Например, R = 2 означает, что КСП может находиться в двух состояниях: {G («good – хорошее») и B («bad – плохое»)}. Если параметр R = 3, то КСП может находиться в трех состояниях: {G, GB, B} и т.д. В общем случае обозначим состояния КСП через переменную С, которая может принимать R значений.

Введем понятие память канала глубины l, которое означает, что существует статистическая связь между текущим состоянием канала С0 и l предшествующими состояниями канала. Эта связь количественно оценива-

ется переходной вероятностью: P(C0 C−1,C−2 ,...C−l ), т.е. вероятность пере-

хода из предшествующего состояния, в котором находился канал С–1, в рассматриваемое (С0) статистически определяется (l – 1) предшествующих состояний, в которых побывал канал связи. Последовательность состояний КСП глубины l – C−1,C−2 ,...,C−l образует состояние памяти КСП

глубины l. Мощность множества состояний памяти канала глубины l определяется как NП = Rl . Для описания дискретного канала с памятью (ДКП)

необходимо задать матрицу переходных вероятностей состояний памяти канала, называемую в дальнейшем матрицей памяти – МП, и множество

матриц ошибок {M 0ν} ν =(1, R) , характеризующих каждое состояние

СДКП.

2.2.1.Стационарныйk-ичныйдискретныйканалспамятьюглубины l

Ниже рассматриваем модели только стационарных ДКП, поэтому определение «стационарный» опускаем.

Матрица памяти ДКП имеет вид:

1 2 … ν…R

:

Rl

МП имеет размерность [Rl ×R], и для каждой ее строки выполняется условие нормирования

2

∑R p( νµ) =1, µ =1, Rl .

ν=1

С учетом условия нормирования размерность матрицы памяти, определяющая минимальное число параметров, однозначно задающих МП и определяемых экспериментально, определяется как

Пример 2.1. ДКП характеризуются двумя состояниями {G, B}={0,1},

т. е. R = 2, глубина памяти l = 2. Тогда матрица памяти имеет вид

Для этого частного случая последовательность смены состояний ДКП такова:

...C−2 ,C−1,C0 → BGB101 .

Согласно (2.10) размерность МП определится по формуле

NП = 22 1 = 4 ,

т. е. переходные вероятности каждого столбца однозначно задают матрицу памяти данного примера.

Как отмечалось выше, каждое состояние ДКП характеризуется своей матрицей ошибок:

C1 C2 ... Cν... CR ,

M 10 M 02 ...M 0ν...M 0R .

3

Размерность каждой матрицы ошибок, как и в случае канала без памяти, равна [k ×k](для k-ичного канала).

Для каждой строки матрицы выполняется условие нормирования:

Вид матрицы ошибок ДКП, находящихся в состоянии Cν :

y1 …yj…yk

С учетом условия нормирования размерность каждой из R матриц ошибок, равная минимальному числу параметров, определяемых экспериментально и однозначно задающих матрицу ошибок, составляет

Суммарное число параметров всех R матриц ошибок

Таким образом, полная размерность модели ДКП, с учетом (2.10) и (2.12), определяется как

рассматриваемого ДКП, согласно (2.13), определяется как NM = 4 +4 =8.

4

2.2.2. Двоичный дискретный канал с памятью глубины l (ДДКП)

Матрица памяти ДДКП с числом состояний R имеет вид

Следовательно, размерность матрицы памяти МП определяется согласно (2.10).

Матрица ошибок ДДКП, находящихся в µ-м состоянии µ = (1, R), имеет вид

выходе ДДКП, находящемся в µ-м состоянии.

Размерность каждой из R матриц ошибок, согласно (2.11), определя-

Пример 2.3. Для данных примера 2.2 определим полную размерность модели ДДКП.

Согласно (2.14) NM = 22 1+2 2 =8.

Для частного случая симметричного двоичного ДКП глубины l (симметричность распространяется на матрицы ошибок ДСДКП) справед-

ливы следующие утверждения: NП определяется из (2.10), N (01) =1 и

Например, для данных предыдущего примера NM = 22 1+2 = 6.

5

Практический интерес представляют модели ДСДКП с числом независимых параметров (размерностью) не более 4–5, т.е. с харак-

теристиками вида: R = 2, l = 1, k = 2 и NM = 21 1+1 2 = 4.

Наиболее популярными моделями, отвечающими этим требованиям, являются модель Гильберта, модель Гильберта–Эллиота, модель Пуртова, которые рассматриваются ниже.

Прежде чем описать упомянутые модели, введем понятие, характерное для симметричных двоичных дискретных каналов с памятью, – пакет ошибок длины b. Это вектор ошибок длины b, первая и последняя компоненты которого всегда равны единице. Число единиц и нулей внутри пакета распределяется произвольно, но при этом число подряд идущих нулей должно быть меньше некоторого числа bЗ, называемого защитным интервалом.

Пример 2.4. Пусть дан некоторый поток ошибок:

….0 0 0 0 1 0 0 1 0 1 1 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0…. b = 9 b = 4 b = 1 b = 3

Пусть bЗ = 3, тогда в данном потоке ошибок можно выделить 4 пакета с длинами соответственно 9, 4, 1 и 3. В литературе иногда вместо термина пакет ошибок используют термин пачка ошибок.

2.2.3. Модель Гильберта

Это трехпараметрическая модель [2], описывающая ДСДКП с глуби-

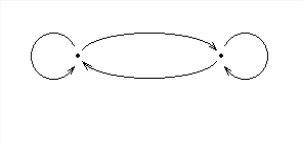
ной памяти l = 1. В основе модели – элементарная цепь Маркова, выделяющая два состояния канала (R = 2): «хорошее состояние» (G), в котором ошибки не возникают, и «плохое состояние» (В), в котором вероятность ошибки в одном разряде составляет рε. Граф марковской цепи показан на рис. 2.5.

Рис. 2.5. Граф переходов состояний ДСДКП модели Гильберта

pBG pε

Матрица памяти канала имеет вид

6

Согласно модели Гильберта матрица ошибок имеет место только в состоянии В:

Таким образом, с учетом (2.15) размерность модели Nм = Nп + N0 = = 2 + 1 = 3, т. е. модель Гильберта полностью описывается тремя парамет-

рами: рε, рGB, рBG, которые должны быть определены экспериментально. Имея указанные параметры, можно аналитически вычислить вероятностные показатели, характеризующие условия передачи информации по ДСДКП с глубиной памяти l =1.

Определим вероятности пребывания канала в состояниях G и B как финальные вероятности марковской цепи:

p(G) = p(G) pGG + p(B) pBG = p(G) pGG + (1 – p(G)) pBG,

p(B) = p(B) pBB + p(G) pGB = p(B) pBB + (1 – p(B)) pGB,

Если pGG или pBB велики, то наблюдается тенденция к сохранению возникшего состояния G или В, что и моделирует канал с пакетными (коррелированными) ошибками. В состоянии В возникает пакет ошибок.

Для вычисления вероятности возникновения ошибок определенной кратности в большинстве моделей ДСДКП, используемых на практике и описываемых простыми цепями Маркова, принимают следующее допущение. Считается, что в различных состояниях памяти канала имеет место биномиальное распределение ошибок, с соответствующей вероятностью ошибки [3]. Тогда, с учетом изложенного, определим вероятность ошибки на символ в ДСДКП:

7

Вероятность ошибки кратности i среди n символов, передаваемых по ДСДКП,

Вероятность искажения кодовой серии длины n

Вероятность ошибки рош определяется из (2.18) и учитывает память канала.

2.2.4. Модель Гильберта – Эллиота

Это четырехпараметрическая модель ДСДКП [2,4] с глубиной памяти l = 1 и числом состояний канала R = 2. В отличие от предыдущей модели в данной модели допускается появление ошибок как в «хорошем» (G), так и в «плохом» (В) состояниях канала соответственно с вероятностями

pε0 и pε1.

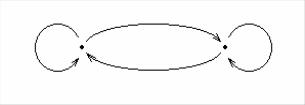
Граф марковской цепи показан на рис. 2.6.

Рис. 2.6. Граф переходов и состояний ДСДКП модели Гильберта – Эллиота

Матрица памяти данной модели аналогична предыдущей. Матрица ошибок в ν-м состоянии памяти канала имеет вид

С учетом (2.16) размерность модели

8

NМ = NП + N0 = 2 · (2 – 1) + 2 = 4.

Модель Гильберта – Эллиота полностью описывается четырьмя па-

раметрами: pε0, pε1, pBG, pGB. Вероятности p(G) и p(B) определяются по

(2.16) и (2.17).

Вероятность ошибки на символ

Вероятности р(i, n) и р (≥1, n) приближенно оцениваются выражениями, аналогичными (2.19) и (2.20).

2.2.5. Модель Пуртова

Модель ДСДКП, предложенная Л.П. Пуртовым [5], является многопараметрической и достаточно сложной. В то же время для практического использования им рекомендуется двухпараметрическая упрощенная модель, которая и будет рассмотрена ниже.

Согласно рассматриваемому подходу вероятность искажения серии из n элементов, передаваемой по каналу с пакетирующимися ошибками, определяется как

Параметры модели: α – коэффициент пакетирования ошибок; р – вероятность ошибки на символ. При α →0 P(≥1, n) np , т. е. выражение

совпадает с оценкой вероятности искажения в канале с независимыми ошибками. При α →1 P(≥1, n) p , т. е. при любом искажении символа

начинается пакет ошибок.

Вероятность ошибки кратности не меньше i в серии длины n,

Вероятность i-кратной ошибки в серии длины n

В заключение отметим, что, как показали экспериментальные исследования, большинство современных коммутируемых телефонных каналов достаточно корректно описывается моделями ДСДКП.