6.2.1. Критерий Гурвица Формулировка критерия: автоматическая система, описываемая характеристическим уравнением n-го порядка

, (6.9)

устойчива, если при a₀>0 положительны все диагональные определители (определители Гурвица) ∆₁, ∆₂, …, ∆_n , т. е.

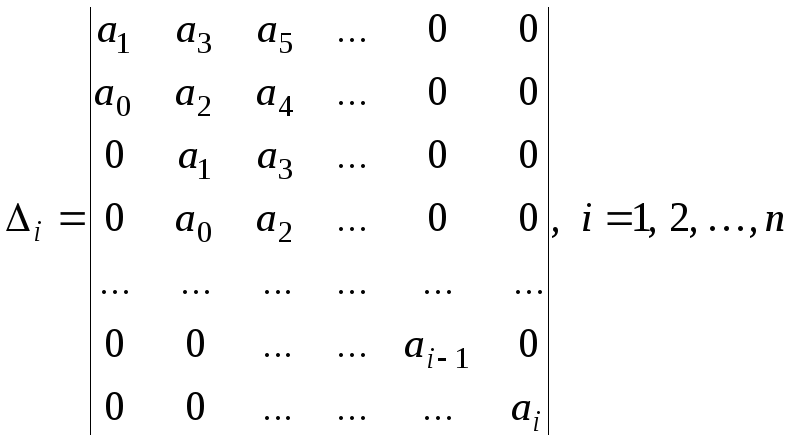, (6.10)

где ∆₁=a₁, ∆₂ = a₁a₂ - a₀a₃, ∆₃ = a₃(a₁a₂ - a₀a₃),… .

Если хотя бы один из определителей Гурвица отрицателен, то система неустойчива. Если главный определитель ∆_п= 0, а все остальные определители положительны, то система находится на границе устойчивости.

Критерий Гурвица удобно применять для систем не выше 4-го порядка. При n>4 целесообразно применять критерий Рауса.

6.2.2. Критерий Рауса

Для оценки устойчивости системы по этому критерию составляется матрица Рауса, представляющая собой таблицу

. (6.11)

Формулировка критерия: САУ будет устойчивой, если будут положительны все элементы первого столбца таблицы Рауса (включая а₀ и а₁), рассчитываемые по выражению:

, (6.12)

где i – номер строки, j – номер столбца.

Если хотя бы один коэффициент первого столбца отрицателен, то система неустойчива. При этом число перемен знака среди этих коэффициентов соответствует числу правых корней характеристического уравнения.

6.3. Частотные критерии устойчивости

6.3.1. Критерий Михайлова

Пусть характеристическое уравнение системы имеет вид (6.9). Заменим в нем оператор p на . Тогда кривой Михайлова будет называться функция вида

. (6.15)

Выделим в (6.15) действительную и мнимую части:

(6.16)

Конформное (подобное) отображение кривой Михайлова на комплексной плоскости Re(ω), Im(ω) носит название годографа Михайлова. Для устойчивости САУ необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от 0 до ∞, начав свое движение с положительной полуоси, последовательно проходил n квадрантов комплексной плоскости, нигде не обращаясь в ноль.

Как следствие из критерия Михайлова вытекает, что корни уравнений (6.16) устойчивых САУ должны чередоваться, поскольку вещественная и мнимая координатные оси должны пересекаться годографом поочередно.

Очевидно, что, если годограф Михайлова не проходит последовательно n квадрантов или начинается не на положительной вещественной полуоси, то система неустойчива.

Рис. 6.4. Годографы Михайлова устойчивых САУ 1…4 порядка

6.3.2. Критерий Найквиста

Критерий Г. Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристике (АФЧХ) разомкнутого контура системы. Найквист в своем критерии рассматривает вспомогательную функцию, определяемую по формуле

, (6.21)

где - частотная передаточная функция разомкнутого контура.

Для физически реализуемых САУ степень полинома не выше степень полинома. Тогда степени числителя и знаменателя в (6.21) одинаковы и равныn.

Полюса этой передаточной функции являются полюсами разомкнутой САУ, а нули - полюсами замкнутой системы. Для устойчивости замкнутой системы необходимо и достаточно, чтобы все нули (6.21) располагались в левой половине комплексной плоскости.

Согласно теореме Коши [19] необходимо на комплексной плоскости выбрать контур (контур Найквиста), который охватывал бы всю ее правую половину, и исследовать, не находятся ли внутри ее какие-либо нули функции (6.21). Конформное отображение контура Найквиста в плоскость сводится к построению на комплексной плоскости вектора (годографа Найквиста), начало которого находится в точке (-1,j0), а конец скользит при изменении частоты от 0 до ∞ по АФЧХ разомкнутой системы .

Объединяя все три случая можно дать следующее определение критерия Найквиста:

система в замкнутом состоянии будет устойчива, если разность между числами положительных и отрицательных переходов годографа разомкнутой системы отрезка действительной оси будет равна m/2, где т – количество корней характеристического уравнения разомкнутой системы, находящихся в правой полуплоскости.