44. Пример получения передаточной функции по формуле Мейсона.

Формула Мейсона с пояснением обозначений в ней.

. где – передаточная функцияi прямого канала (i-прямой путь, связывающий вход Х_к с выходом У_l); m- число прямых путей; 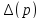– определитель графа( полином, характризуюший совокупность всех замкнутых цепей системы, содержащих обратные связи).;дляi-прямого пути.

Схема САУ в виде сигнального графа.

Сигнальный граф системы управления представляет собой ориентированный граф – совокупность дуг, изображающих отдельные звенья и указывающих направление передачи сигнала, и вершин, соответствующих входным и выходным сигналам звеньев. Отдельному звену алгоритмической схемы, изображаемому прямоугольником, на сигнальном графе системы соответствует стрелка, соединяющая вершины х и у. Около стрелки указывается передаточная функция звена.

Пр:

P1=W1W2W3W4; P2=W5W6W7W8;

L1=W2W02;L2=W3W03; L3=W6W06; L4=W7W07;

1- L1-L2-L3-L4+L1L3+L1L4+L2L3+L2L4;

1=1-L3-L4; 2=1-L1-L2

Ф(р)=

45. Методы описания многомерных линейных сау.

Метод «вход-выход».

Передаточной функцией W(p) называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях. Переходной функцией h(t) называют изменение выходной величины y(t) во времени, возникающее после подачи на вход единичного ступенчатого воздействия, при нулевых начальных условиях.

Импульсной переходной функцией (t(весовая хпрактеристика) называют изменение выходной величины y(t), возникающее после подачи на вход дельта – функции, при нулевых начальных условиях (см. рис.).

Импульсная переходная функция (t) равна производной от переходной функции h(t):

,

Частотные характеристики описывают передаточные свойства элементов и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Зная частотную характеристику элемента, можно определить реакцию элемента на гармоническое воздействие любой частоты, а также на сумму гармонических воздействий различной частоты.

1. Передаточная функция звена (W(p)).

2. Амплитудная частотная характеристика (АЧХ).

3. Фазовая частотная характеристика (ФЧХ).

4. Амплитудно-фазовая характеристика (АФХ).

5. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ).

Зависимость отношения амплитуд выходного и входного сигнала от частоты называют амплитудной частотной характеристикой (сокращенно - АЧХ) и обозначают А() (см. рис.а). Зависимость фазового сдвига между входным и выходным сигналами от частоты называют фазовой частотной характеристикой (ФЧХ) и обозначают () (см. рис.б).

АЧХ показывает, как элемент пропускает сигналы различной частоты. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах в установившемся режиме.

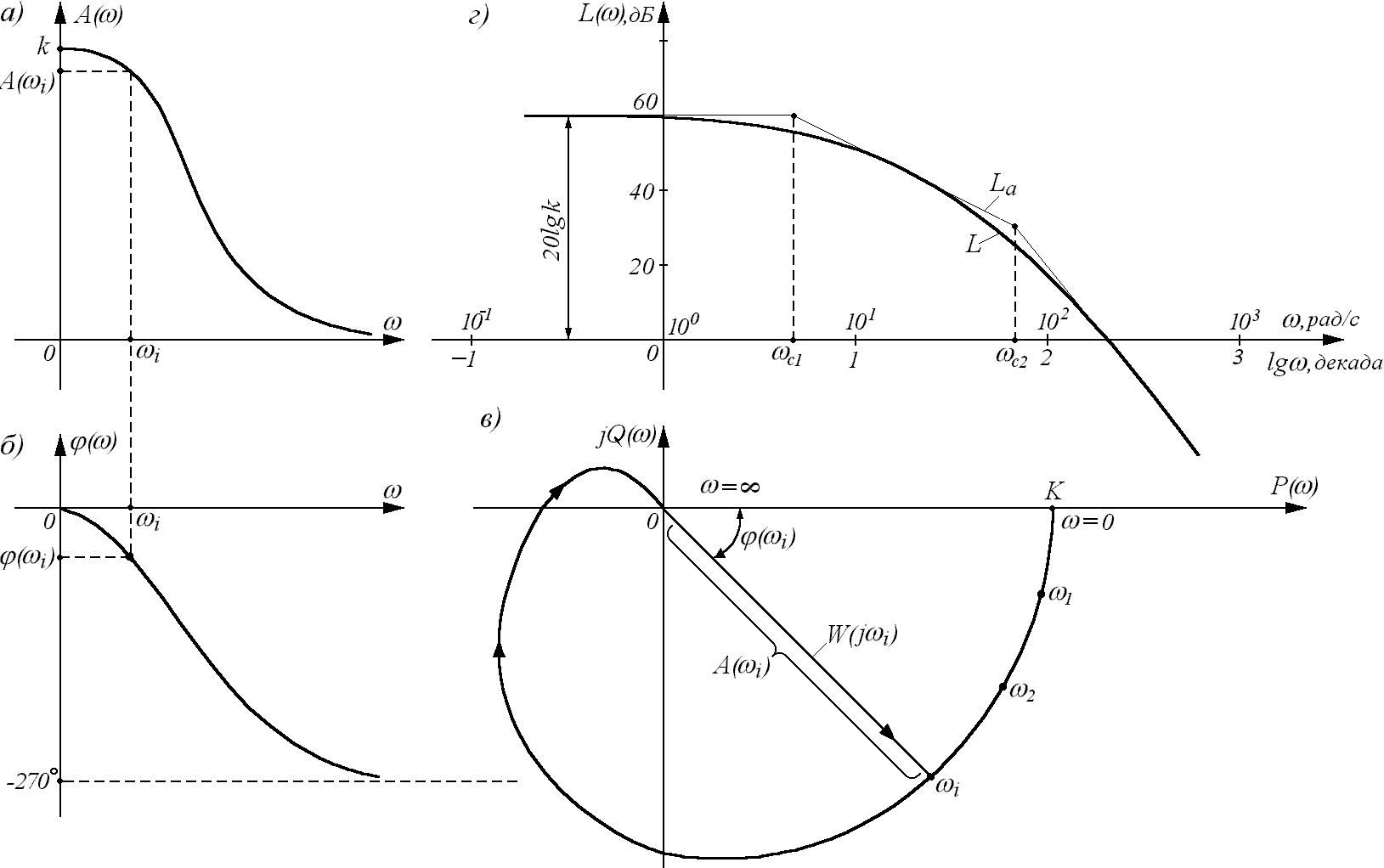
45.1. Амплитудно-фазовая частотная характеристика W(j) представляет собой функцию комплексного переменного j, модуль которой равен А(), а аргумент равен (). Каждому фиксированному значению частоты _i соответствует комплексное число W(j_i), которое на комплексной плоскости можно изобразить вектором, имеющим длину А(_i) и угол поворота (_i) (см. рис.в). Отрицательные значения (), соответствующие отставанию выходного сигнала от входного, принято отсчитывать по часовой стрелке от положительного направления действительной оси. Аналитическое выражение для АФХ конкретного элемента можно получить из его передаточной функции путем подстановки р=j: АФХW(j), как и любая комплексная величина, может быть представлена в показательной форме Связь между различными частотными функциями следующая:

При практических расчетах автоматических систем удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков.

За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервал частот, заключенный между произвольным значением _i и его десятикратным значением 10_i. Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ) координаты которой измеряют в логарифмических единицах – белах (Б) или децибелах (дБ).

На рис.г показаны ЛАЧХ L() (толстая линия) и соответствующая ей приближенная (асимптотическая) характеристика L_а() в виде прямолинейных отрезков (тонкая линия). Частоты, соответствующие точкам стыковки отрезков, называют сопрягающими и обозначают _с.