28. Регуляторы суим.

1. Аналоговые регуляторы класса “вход-выход” на основе операционных усилителей

Независимо от технологического назначения регуляторов все они подразделяются на 2 больших класса:

- параметрические регуляторы класса «вход/выход» (П- , ПИ-, ПИД- и т. п. регуляторы );

- регуляторы состояния САУ (апериодические, модальные и т.п.).

Первый класс регуляторов на функциональных схемах СУ ЭП обозначается в виде переходной функции.

1. Пропорциональный регулятор (П-регулятор).

Принципиальная схема регулятора приведена на рис. 4.19.

Будем полагать, что на входе регулятора - сигнал ошибки регулирования Х_вх , причемХ_вх =Х_з-Х_ос. При этом вместо двух резисторовR_ЗиR_ос используется один -R_вх .

Передаточная функция регулятора

Временная характеристика регулятора:

У_вых(t)=К_регХ_вх(t).

2. Интегральный регулятор (И-регулятор).

Принципиальная схема регулятора приведена на рис. 4.22.

Рис. 4.22. Принципиальная электрическая схема интегрального регулятора

Передаточная функция регулятора

(4.50)

где T_И- постоянная времени интегратора,T_И =R_ВХС₀.

Временная характеристика регулятора:

У_вых(t)= У_вых(0)+1/( R_ВХС₀)Х_вх(t)t.

Переходный процесс в регуляторе при нулевых начальных условиях (У_вых(0)=0) будет иметь вид, изображенный на рис. 4.23.

Функциональная схема интегрального регулятора приведена на рис. 4.24.

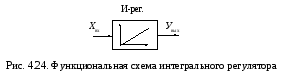3. Дифференциальный регулятор (Д-регулятор).

Принципиальная схема регулятора приведена на рис. 4.25.

Передаточная функция регулятора

(4.51)

где T_Д- постоянная времени интегратора,T_Д =R₀С_ВХ.

Временная характеристика регулятора:

У_вых(t)=T_Д(t),

где (t) - дельта-функция Дирака.

Переходный процесс в регуляторе будет иметь вид, изображенный на рис. 4.26.

Следует отметить, что ограниченная полоса пропускания частот самих операционных усилителей не позволяет реализовать чистое (идеальное) дифференцирование. Кроме того, в силу низкой помехозащищенности дифференциальных регуляторов сложилась практика применения реальных дифференцирующих звеньев и принципиальные схемы таких регуляторов несколько отличаются от приведенной на рис. 4. 25.

Функциональная схема дифференциального регулятора приведена на рис. 4.27.

4. Пропорционально-интегральный регулятор (ПИ-регулятор).

4. Пропорционально-интегральный регулятор (ПИ-регулятор).

Принципиальная схема регулятора приведена на рис. 4.28.

Передаточная функция регулятора

(4.52)

где K_РЕГ- коэффициент передачи регулятора,K_РЕГ =R₀/R_ВХ;

T_И- постоянная времени интегратора,T_И =R_ВХС₀.

Временная характеристика регулятора:

У_вых(t)= У_вых(0) + ( K_РЕГ + t/( R_ВХС₀))Х_вх(t).

Переходный процесс в регуляторе при нулевых начальных условиях будет иметь вид, изображенный на рис. 4.29.

Передаточную функцию пропорционально-интегрального регулятора часто представляют не в виде суммы двух слагаемых, а в виде так называемого изодромного звена

, (4.53)

где T_ИЗ- постоянная времени изодромного звена,T_ИЗ=R₀C₀,

T_И- постоянная времени интегрирования регулятора,T_И=R_ВХC₀ .

ПИ-регулятор, включенный в структуру САУ, обеспечивает компенсацию одной большой постоянной времени объекта управления (см. раздел 8.1).

1. Пропорционально-дифференциальный регулятор (ПД-регулятор) Принципиальная схема регулятора приведена на рис. 4.31.

Передаточная функция регулятора

(4.54)

где K_РЕГ - коэффициент передачи регулятора,K_РЕГ =R₀/R_ВХ;

T_Д- постоянная времени интегратора,T_Д =R₀С_ВХ.

Временная характеристика регулятора:

У_вых(t)= K_РЕГ X_вх(t) +T_Д(t),

где (t) - дельта-функция Дирака.

Переходный процесс в ПД- регуляторе будет иметь вид, изображенный на рис. 4.32, функциональная схема регулятора приведена на рис. 4.33.

Рис. 4.32. Переходный процесс в ПД- регуляторе

6. Пропорционально-интегрально-дифференциальный регулятор (ПИД-

регулятор)

Принципиальная схема регулятора приведена на рис. 4.34.

Передаточная функция регулятора

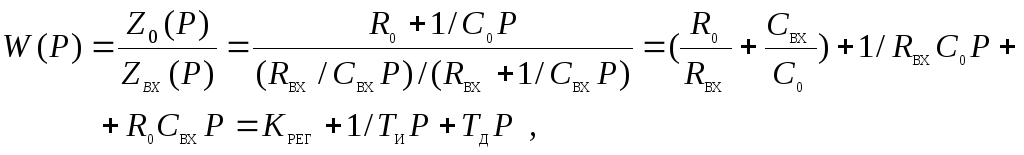(4.55)

где K_РЕГ - коэффициент передачи регулятора,K_РЕГ =R₀/R_ВХ +C_ВХ/С₀;

T_И- постоянная времени интегрирования,T_И =R_ВХС₀;

T_Д- постоянная времени дифференцирования,T_Д =R₀С_ВХ.

Временная характеристика регулятора:

У_вых(t)= У_вых(0) +K_РЕГ X_вх(t) + (1/T_ИP) X_вх(t) + T_Д(t),

где (t) - дельта-функция Дирака.

Переходный процесс в регуляторе будет иметь вид, изображенный на рис. 4.35, функциональная схема приведена на рис. 4.36.

По аналогии с ПИ-регулятором ММ ПИД-регулятора часто представляют в виде изодромного звена второго порядка

, (4.56)

где Т_ИЗ,1 , Т_ИЗ,2 - постоянные времени изодромного звена;Т_ИЗ,1 = R₀С₀ , Т_ИЗ,2 = =R_вхС_вх.

ПИД-регулятор обеспечивает компенсацию двух больших постоянных времени объекта управления, обеспечивая интенсивность динамических процессов в САУ.