8. Метод пространства состояний

Широкое распространение компьютеров и мощных систем программирования побуждает к исследованию САУ во временной области, а, следовательно, к непосредственному использованию описания динамических систем управления в форме обыкновенных дифференциальных уравнений без перехода к операторной форме. Кроме того, как уже отмечалось, векторно-матричные формы описания и исследования применимы не только к одномерным, линейным, стационарным САУ, но и к широкому классу многомерных, нелинейных и нестационарных САУ.

Чтобы получить пригодную для компьютерного синтеза и анализа модель САУ, необходимо представить ее в переменных состояния системы, используя далеко не единственный набор переменных. Следует отметить, что описание систем во временной области в векторно-матричной форме лежит в основе современной теории управления и оптимизации. В настоящей главе рассмотрены вопросы применения метода пространства состояния к непрерывным системам управления.

8.1. Векторно-матричное описание сау

Состояние системы– это совокупность значений переменных системы (координат состояния), существенных с точки зрения решаемой задачи. В общем случае, в это число включают не только выходные и внутренние переменные САУ, но и задающие воздействия, и доминирующие возмущающие воздействия внешней среды. Чем полнее достоверной информации о состоянии системы в текущий момент времени, тем проще определить будущие значения всех ее переменных. Инженерно-технический персонал, разрабатывающий и эксплуатирующий технические системы управления, оперирует, как правило, с такими физическими переменными, которые могут быть измерены с помощью соответствующих датчиков. К таким физическим переменным САУ относят ускорение, скорость, перемещение, давление, расход, температуру, уровень и т. п. Координатами датчиков технологических координат САУ являются другие переменные - напряжение, ток, частота следования импульсов, двоичный код и т. п., что дает исследователю возможность выбора для синтеза и анализа необходимого набора координат состояния САУ.

Векторно-матричная модельмногомерной, нелинейной, нестационарной САУ записывается в виде [6, 10, 11, 19]

,

, (8.1)

где X(t),U(t), F(t),Y(t) – соответственно векторы состояния, управления, возмущения и выходных (управляемых) координат системы,

– вектор первых производных координат состояния,

– нелинейные, нестационарные функции координат состояния, управления и возмущения системы.

В уравнении (8.1) вектор управления U(t) является, в общем случае, некоторой нелинейной нестационарной функцией задающих координат, координат состояния и возмущения САУ и призван обеспечить оптимальное управление системой. Описание многомерных, нелинейных, нестационарных САУ в форме (8.1) не позволяет, как правило, получить инженерное решение задачи структурно-параметрического синтеза оптимального управленияU(t) или такое решение приводит к неоправданным затратам на реализацию (в техническом или экономическом аспектах). В большинстве случаев такие модели сводят к одномерным или многомерным линейным (линеаризованным) квазистационарным моделям, для которых имеются развитые методы и инженерные методики синтеза оптимального управления.

Линейную (линеаризованную) модельмногомерной стационарной (квазистационарной) САУ представляют в виде системы обыкновенных дифференциальных уравнений первого порядка в форме Коши:

,

, (8.2)

……………………………………………………

.

Эту же систему дифференциальных уравнений можно представить в векторно-матричной форме [6, 11, 19]:

, (8.3)

где - векторы (векторы-столбцы) соответственно состояния и управления САУ,

,;

- символ транспонирования (иногда для обозначения транспонирования применяют буквенный символ “т”);

- стационарные матрицы соответственно состояния и управления,

,.

В общем случае, на объект управления помимо управляющих воздействий действуют возмущающие воздействия. В этом случае векторно-матричную модель системы представляют в виде

, (8.4)

где - вектор-столбец возмущающих воздействий САУ,C– стационарная матрица возмущений,

,

.

Выходные (управляемые) переменные не всегда непосредственно принадлежат вектору состояния. В линейных САУ они линейно связаны с переменными состояния, управляющими и возмущающими переменными. В этом случае к уравнениям (8.3), (8.4) присоединяют алгебраические линейные уравнения

(8.5)

или , (8.6)

где - вектор выходных переменных САУ,;

K,L,M– стационарные матрицы соответственно размерностей (rn), (rm), (rd).

Следует отметить, что приведенные уравнения (8.1)…(8.6) дают описание лишь объекта управления или разомкнутой системы, если вектор управленияU(t) не является функцией координат состояния САУ. В замкнутых линейных САУ управление обычно формируют как линейную форму координат состояния и, в общем случае, возмущения САУ.

В качестве примера приведем векторно-матричное описание ранее рассматриваемого электродвигателя постоянного тока как объекта регулирования по цепи якоря. Пусть выходной (регулируемой) координатой является скорость вращения двигателя. Полагая, что напряжение возбуждения , а магнитный поток, математическую модель электродвигателя можно представить в виде:

,

. (8.7)

Воспользуемся векторно-матричной моделью линейных САУ в виде (8.4), (8.5). Зададимся векторами состояния, управления и возмущения в виде:

;;

(8.8)

По уравнениям (8.7) найдем матрицы состояния, управления и возмущения:

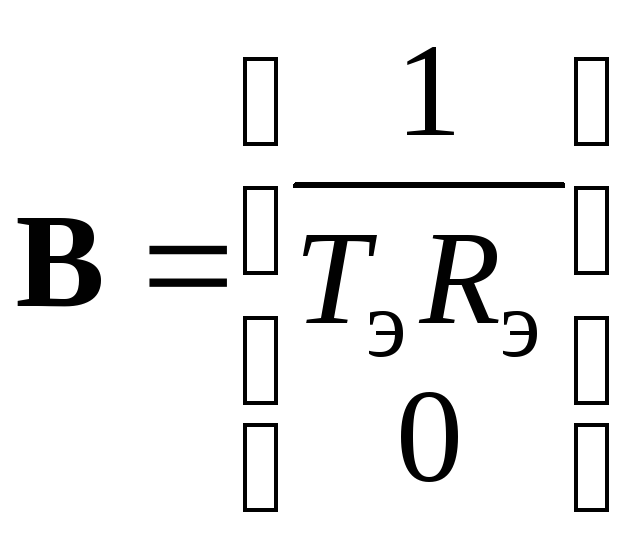;;. (8.9)

Поскольку выходная переменная всего одна и ей является координата состояния , уравнение выхода преобразуется к скалярной форме

. (8.10)

По описанию системы в форме векторно-матричных уравнений (ВМУ) можно непосредственно получить эквивалентную передаточную функцию (ПФ) и, наоборот, зная ВМУ системы, можно получить ее ПФ. Для этого в системе MATLABимеется две функции: функцияtf и функция ss.

Пусть ВМУ системы имеет вид (8.3), (8.5). Применительно к системе MATLABВМУ записывают в виде

(8.11)

Для получения ВМУ в системе MATLABнеобходимо определить функциюss(A,B,C,D). Для преобразования ВМУ к ПФ системы необходимо записать:

sys­_ss=ss(A,B,C,D); % Формирование ВМУ системы;

sys_tf=tf(sys­_ss), % Преобразование ВМУ к ПФ системы.

Для обратного преобразования ПФ к ВМУ необходимо записать:

sys_tf=tf(num,den); % Формирование ПФ системы;

sys_ss=ss(sys_tf); Преобразование ПФ к ВМУ системы.

Рассмотрим пример. Пусть ПФ системы имеет вид

.

Тогда запишем скрипт преобразования ПФ к ВМУ и обратного преобразования ВМУ к ПФ:

num=[0.4];

den=[1 2 1 0.6];

sys_tf=tf(num,den); % Формирование ПФ системы;

sys_ss=ss(sys_tf); %Преобразование ПФ к ВМУ системы;

a =

x1 x2 x3

x1 -2 -0.5 -0.075

x2 2 0 0

x3 0 4 0

b =

u1

x1 0.25

x2 0

x3 0

c =

x1 x2 x3

y1 0 0 0.2

d =

u1

y1 0

sys_tf=tf(sys_ss) % Преобразование ВМУ к ПФ системы

Transfer function:

0.4

--------------------- .

s^3 + 2 s^2 + s + 0.6