5.2. Типовые динамические звенья и структурные схемы сау

Для наглядного представления структуры сложной динамической системы управления как совокупности элементов и связей между ними применяют структурные схемы и графы. Структурные схемы, как и сигнальные графы, представляют собой графическое изображение структуры САУ. Элементы структурной схемы САУ представляют в виде типовых динамических звеньев, характеризующихся однонаправленностью, одним входом и одним выходом, что позволяет применить для их описания аппарат передаточных функций. Если реальное динамическое звено не обладает однонаправленностью, т. е. выход оказывает влияние на вход, то такой элемент представляют в виде направленного звена с обратной связью. Если у элемента несколько входов, в его структуру включают суммирующие звенья (сумматоры) – специфические многовходовые безынерционные звенья с единичными коэффициентами передачи по каждому входу, причем каждый вход сумматора обозначается знаковой функцией (+ или –). Если у элемента несколько выходов, это означает, что его нельзя рассматривать как элементарное звено и к нему необходимо применить декомпозицию, выделив соответствующие числу выходов звенья.

На структурных схемахдинамические звенья изображают прямоугольниками, входные и выходные воздействия - подходящими и отходящими от прямоугольников стрелками и текстовыми надписями, обозначающими формальный их вид. Внутри прямоугольников вводят обозначения передаточных функций звеньев. Сумматоры сигналов (переменных САУ), как правило, обозначают окружностями, сами сигналы - подходящими к окружностям стрелками с указанием имен переменных и знаков алгебраического суммирования (+ или –). Следует отметить, что в технической литературе, компьютерных системах автоматизированного проектирования и управления, системах сопровождения жизненного цикла САУ (САПР, АСУ ТП,CAD/CAM,SCADA,CALS) встречается множество графических обозначений сумматоров сигналов, однако в силу своей простоты все они интуитивно понятны.

В обобщенной форме структурная схема динамического звена приведена на рис. 5.3.

Рис. 5.3. Обобщенная структурная схема динамического звена

Типовые элементарные динамические звенья,их реакции на единичные ступенчатое и импульсное воздействия приведены в табл. 5.2.

В качестве примера составления структурных схемдинамических объектов управления рассмотрим электродвигатель постоянного тока, регулируемый по цепям якоря и возбуждения [3, 18]. Функциональная схема и схемы замещения электродвигателя приведены на рис. 5.4.

В структуре электродвигателя можно выделить три основных цепи (см. рис. 5.4б, 5.4в, 5.4г):

- цепь якоря, питаемая регулируемым напряжением U_я;R_э,L_э– соответственно эквивалентное активное сопротивление и эквивалентная индуктивность якорной обмотки;E_д– э.д.с. электродвигателя;i_я– ток якоря;

- цепь возбуждения, питаемая регулируемым напряжением U_в;R_в,L_в– соответственно эквивалентное активное сопротивление и эквивалентная индуктивность обмотки возбуждения;i_в– ток возбуждения;

- электромеханическая цепь, обеспечивающая преобразование электромагнитной энергии в механическую энергию вращения вала ротора; J_д– приведенный к валу двигателя момент инерции электродвигателя и вращаемого механизма;M,M_c– соответственно электромагнитный момент электродвигателя и момент сопротивления на его валу; - скорость вращения вала двигателя.

Таблица 5.2

Название звена и его передаточная функция W(p)	Переходный процесс h(t)	Импульсный переходный процесс w(t)
1. Масштабирующее (безынерционное) звено W(p) = k	h(t) 0 t	w(t) 0 t
2. Интегрирующее звено	h(t) 0 t	w(t) 0 t
3. Идеальное дифференцирующее звено W(p) = kp	h(t) 0 t	w(t) 0 t
4. Реальное дифференцирующее звено	h(t) 0 t	w(t) 0 t
5. Апериодическое звено	h(t) k 0 T t	w(t) 0 T t
6. Колебательное звено	h(t) k 0 t	w(t) 0 t
7 . Изодромное звено	h(t) 0 t	w(t) 0 t

Для описания динамических моделей электрических цепей электродвигателя воспользуемся законами Кирхгофа, а для описания механической цепи – 2-м законом Ньютона. Тогда получим:

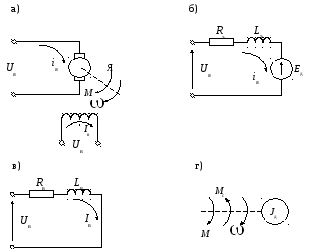
Рис. 5.4. Функциональная схема (а) и схемы замещения (б-г)

электродвигателя постоянного тока

,

, (5.9)

,

где ,- электромагнитные постоянные времени соответственно обмотки якоря и обмотки возбуждения,,.

Электромагнитные цепи двигателя взаимосвязаны. При подаче напряжения по цепи якоря протекает ток, создающий электромагнитный момент, вращающий ротор, т. е.

, (5.10)

где - конструктивная постоянная двигателя.

Ток, протекающий по обмотке возбуждения, создает магнитный поток Ф, пронизывающий обмотку якоря и наводящий в ней э.д.с. вращения, т. е.

, (5.11)

где - конструктивная постоянная двигателя, в системе СИ равная по величине.

Анализируя выражения (5.10), (5.11), заметим, что произведение переменных приводит к нелинейности математической модели электродвигателя, регулируемого одновременно по цепям якоря и возбуждения. Полагая, что электродвигатель регулируется только по цепи якоря (напряжение возбуждения ,), математическая модель электродвигателя примет вид линейной модели 2-го порядка

, (5.12)

.

Для перехода от дифференциальных уравнений (5.12) к операторным уравнениям произведем замену . Тогда получим

, (5.13)

.

По операторным уравнениям (5.13) составим структурную схему электродвигателя, приведенную на рис. 5.5.

Рис. 5.5. Структурная схема электродвигателя,

регулируемого по цепи якоря

Как видим, структурная схема электродвигателя содержит 4 типовых линейных динамических звена: апериодическое, интегрирующее и 2 безынерционных звена, а также 2 суммирующих элемента.