1. Плавление

Плавление – это процесс перехода твердой фазы вещества в жидкую.

В этом случае уравнение Клапейрона – Клаузиуса примет вид

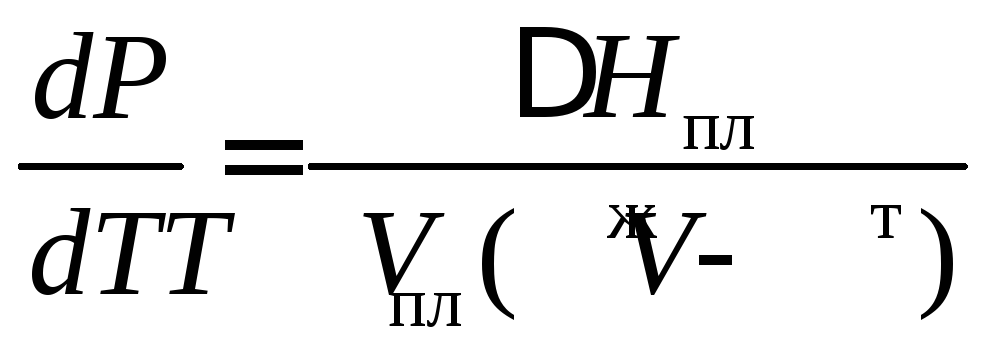, (2)

где Н_пл – теплота плавления всегда положительна, так как при таком

переходе тепло всегда передается системе;

Т_пл – температура плавления вещества;

V ^ж, V ^т – объем жидкой и твердой фазы.

Следовательно, знак производной зависит от разности объемовV ^ж и V ^т (жидкой и твердой фазы).

Если при плавлении объем увеличивается, т.е. V ^ж > V ^т, то с ростом давления температура плавления будет повышаться.

Если же при плавлении объем уменьшается V ^ж < V ^т, то с повышением давления температура должна понижаться.

У большинства веществ разность (V ^ж – V ^т) положительна. Исключение составляют вода, висмут, галлий, для которых плотность жидкости при температуре плавления больше плотности твердой фазы.

Учитывая сравнительно слабую зависимость температуры перехода между конденсированными фазами от давления, можно записать

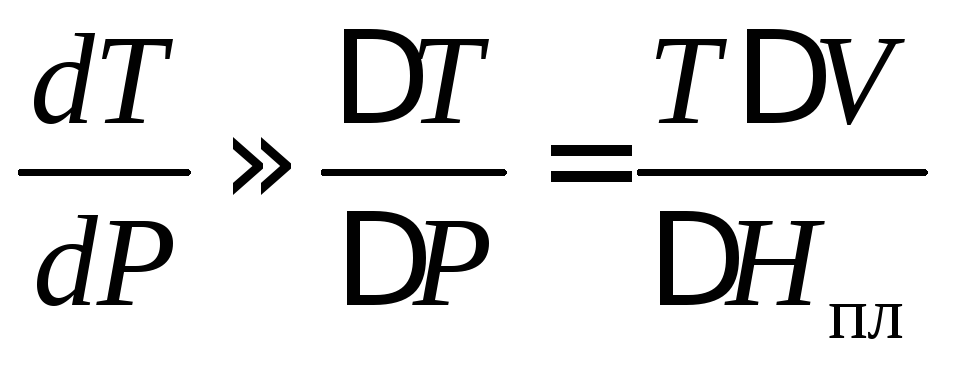. (3)

Пример 1. Плотности () жидкого и твердого олова при температуре плавления (231,9⁰С) соответственно равны 6,988 г/см³ и 7,184 г/см³. Теплота плавления олова равна 7070 Дж/моль. Определить температуру плавления олова под давлением 100 атм.

Решение.

Определим изменение температуры плавления при повышении давления на 1 атм, т.е. .

Из уравнения Клапейрона – Клаузиуса

.

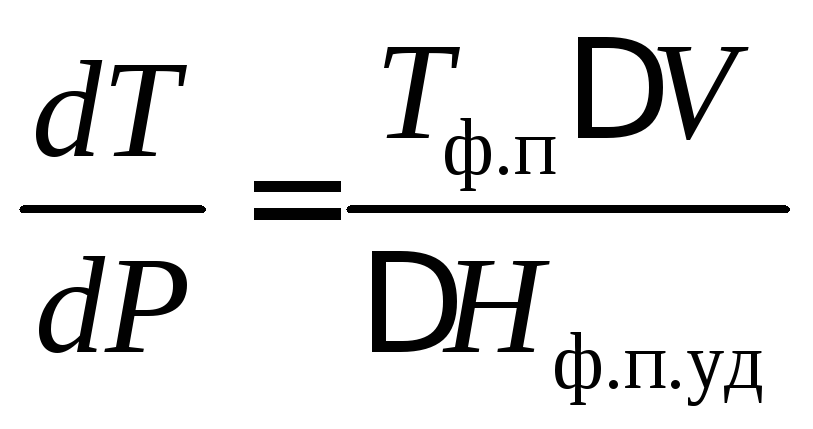В соответствии с условием здесь:

Т_ф.п – температура плавления под давлением 1 атм;

V – разность объемов (удельных) жидкого и твердого олова;

Н_ф.п.уд – удельная теплота плавления олова.

Для нашего случая

Т_ф.п = 231,9 + 273 = 504,9К,

, тогда ,.

В условии задачи дана молярная теплота плавления. Ее необходимо перевести в удельную теплоту плавления, так как М_r (Sn) = 118,7 г/моль, то

.

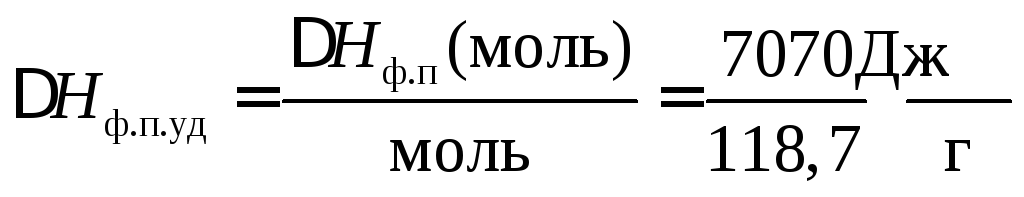Учитывая, что , то

.

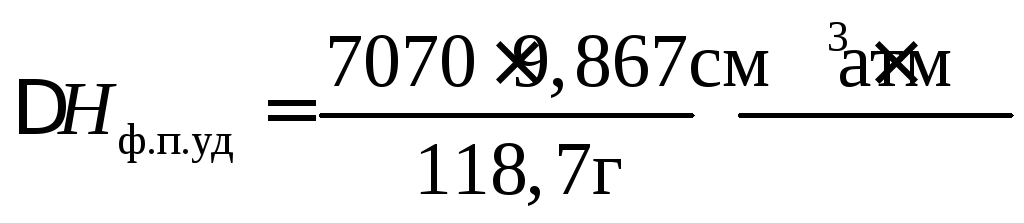После подстановки получаем:

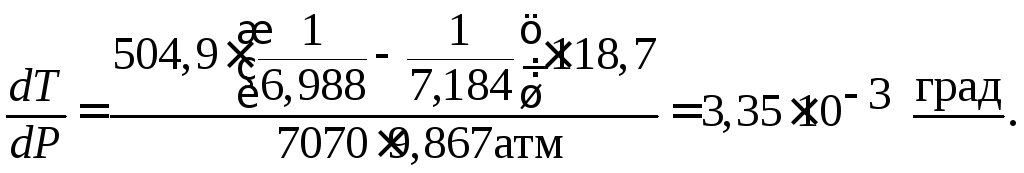
Это значит, что при повышении давления на 1 атм температура плавления олова увеличится на 3,35∙10^-3 град.

Температура плавления олова под давлением 100 атм будет равна

.

Пример 2. Удельный объем (V) льда при 0⁰С равен 1,091 см³/г, а воды 1 см³/г. Теплота плавления льда равна 34,292 Дж/г. Как изменится Т_пл льда при изменении давления на 1 атм? При какой температуре плавится лед под давлением собственного насыщенного пара 4,6 мм.рт.ст?

Решение.

Воспользуемся уравнением Клапейрона – Клаузиуса. Надо определить

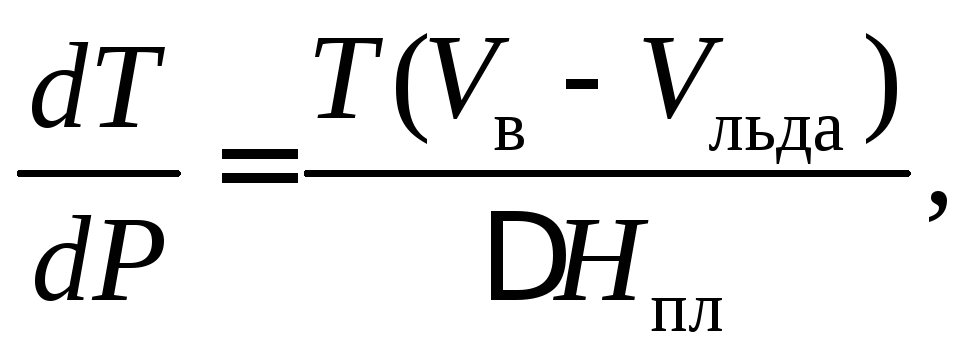
так как имеет размерность град/атм, а величина (V_в – V_льда) см³/г, то величина Н_пл должна быть выражена в атм·см³/г. Учитывая, что , то получаем

Следовательно, если давление возрастает на 1 атм, температура плавления понижается на 0,073⁰С.

Если давление уменьшается с 1 атм до 4,6 мм.рт.ст (), то

–температура плавления повысится на 0,0726⁰С.

Пример 3. Под давлением 0,1013 МПа лед плавится при температуре 273К. Удельный объем льда при 273К равен 991,1∙10^-3 см³/г, а воды – 916,6∙10^-3 см³/г. Молярная теплота плавления льда равна 6010 Дж/моль. Вычислить давление, при котором лед будет плавиться при 271К.

Решение.

Воспользуемся уравнением Клапейрона – Клаузиуса:

,

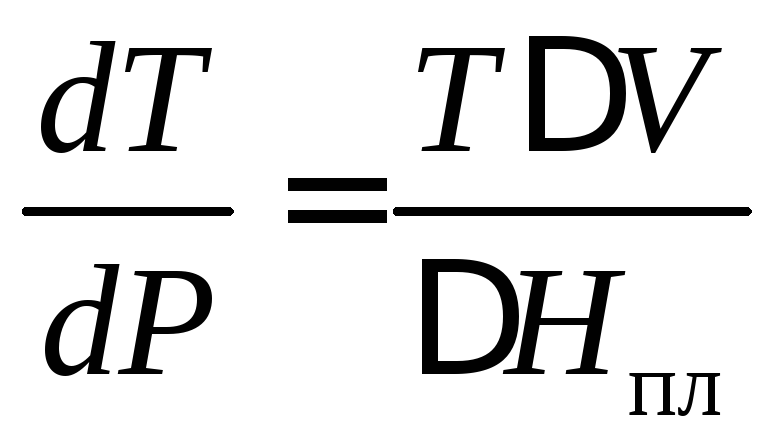где V = V_ж – V_т = 916,6 ∙ 10^-3 – 991,1 ∙ 10^-3 = –74,5 ∙ 10^-3 см³/г – знак минус показывает, что при плавлении льда объем системы уменьшается;

Н_пл – теплота плавления. В задаче дана молярная теплота плавления. Необходимо перевести в удельную теплоту плавления.

Мr (Н₂О) = 18,01 г/моль, тогда

,

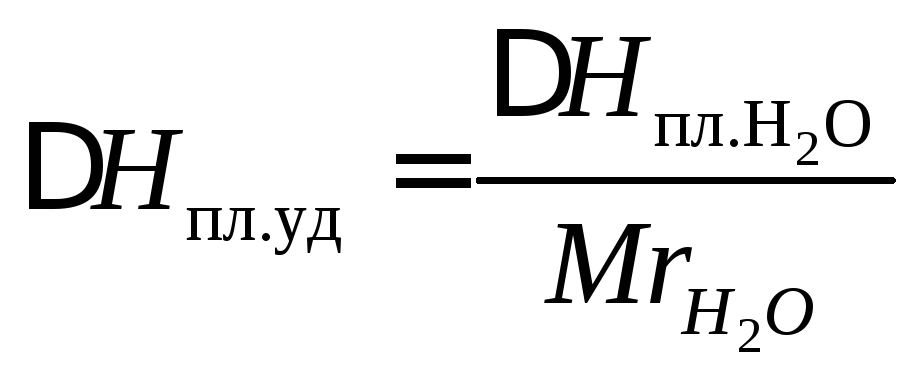
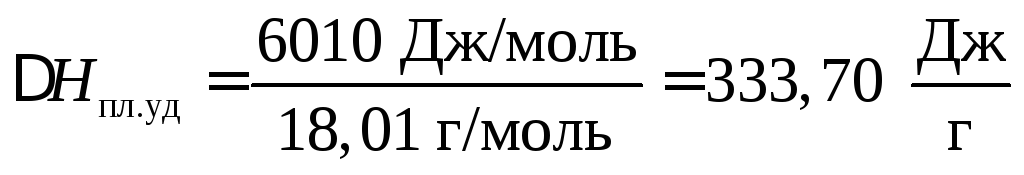но для зависимости единицы измерения –, и 1Дж = 9,867см³∙атм.Или 1 Дж = 9,867 ∙ 0,1013 см³ МПа.

ТогдаН_пл = 333,70 ∙ 9,867 ∙ 0,1013 .

Рассчитаем

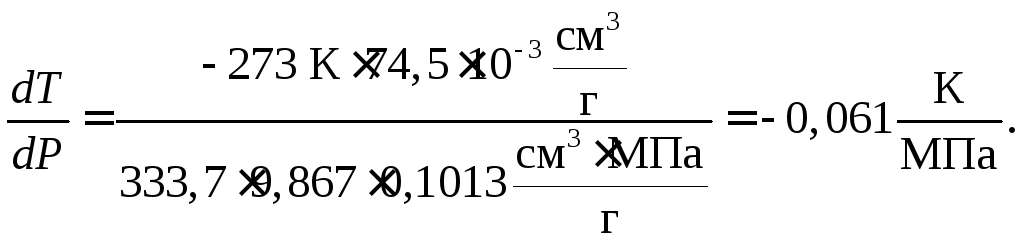
Отрицательное значение зависимости показывает, что при увеличении давления () температура плавления льда понижается ().

Давление, при котором лед будет плавиться при 271К найдем из уравнения (3) .

Отсюда 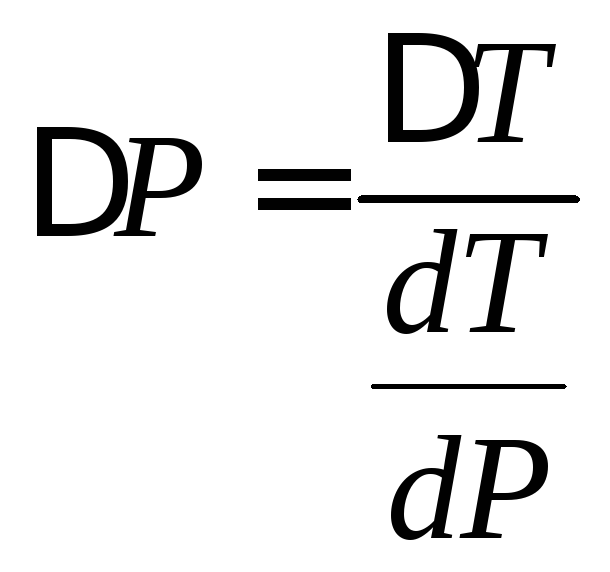, ноТ = (271–273) К = – 2К, а рассчитано ранее (), таким образом

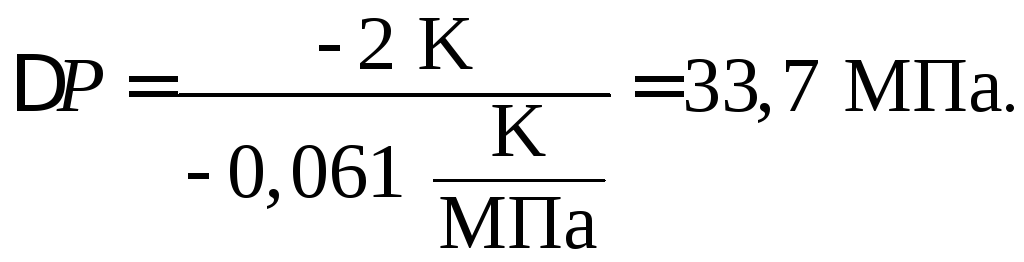
Следовательно Р = Р₀ + Р = 0,1013 + 33,7 = 33,8 (МПа) – при давлении 33,8 МПа лед будет плавиться при 271К.