
- •1. Краткие сведения из теории вероятностей
- •Функция распределения и плотность распределения случайной величины
- •Меры положения и рассеяния кривой распределения
- •1.3. Начальные и центральные моменты
- •1.4. Коэффициенты относительного рассеяния и относительной асимметрии
- •1.5. Квантили распределения
- •1.6. Интервальные оценки истинного значения
- •1.7. Методы оценки точности результатов
- •1.8. Точечные диаграммы и практические кривые распределения размеров
- •1.9. Теоретические законы распределения
- •1.9.1. Закон нормального распределения (закон Гаусса)
- •Кривая Гаусса имеет следующие особенности.
- •1.9.2. Усеченное нормальное распределение
- •1.9.3. Экспоненциальное распределение
- •1.9.4. Распределение Эрланга
- •1.9.5. Логарифмически нормальное распределение
- •1.9.6. Распределение Вейбулла
- •1.9.7. Закон равной вероятности
- •1.9.8. Закон Релея (эксцентриситета)
- •Основными параметрами закона Релея являются:
- •1.9.9. Треугольный закон распределения (закон Симпсона)
- •1.10. Статистическое регулирование технологического процесса
- •1.11. Проверка статистических гипотез
- •1.12. Композиция законов распределения и суммирование погрешностей
- •Контрольные вопросы к главе 1
1.9.2. Усеченное нормальное распределение
Усеченное нормальное распределение случайной величины – это такое распределение, для которого в крайних областях (х < а, х > b) плотность распределения принимается равной нулю; при этом усеченное распределение принимает вид:
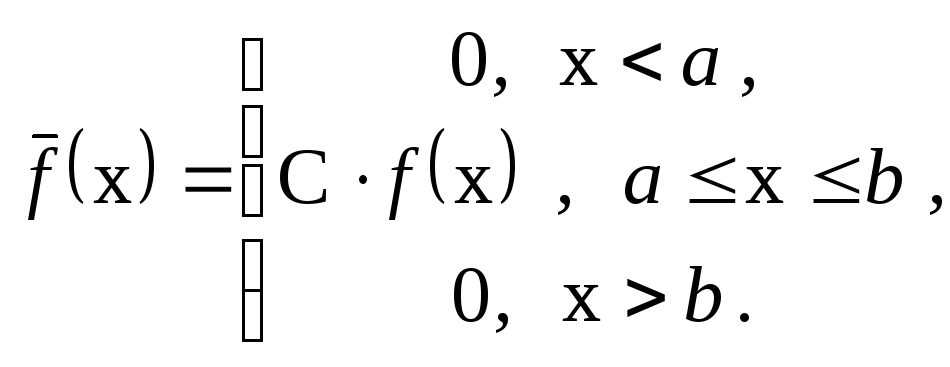 (1.37)
(1.37)
Из условия нормировки
![]()
следует формула для коэффициента
C = 1/ [F(b) – F(a)], (1.38)
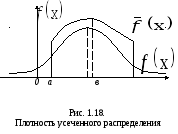
где F функция основного (не усеченного) распределения. Указанные распределения представлены на рис. 1.18.
Приведем основные формулы для усеченного распределения:
![]() ,
,
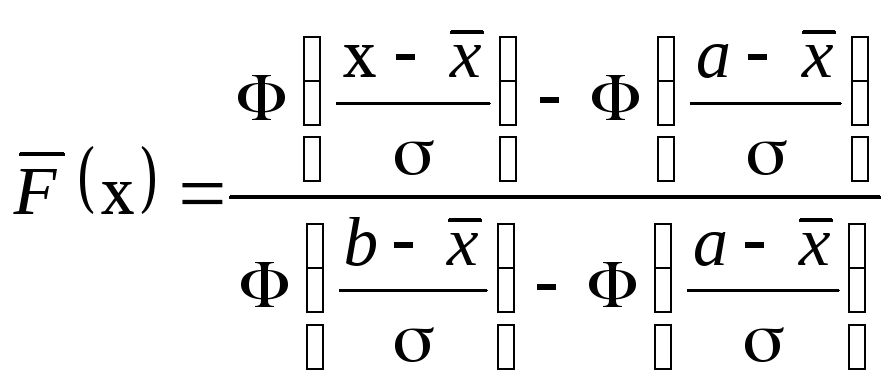 ,
(1.39)
,
(1.39)
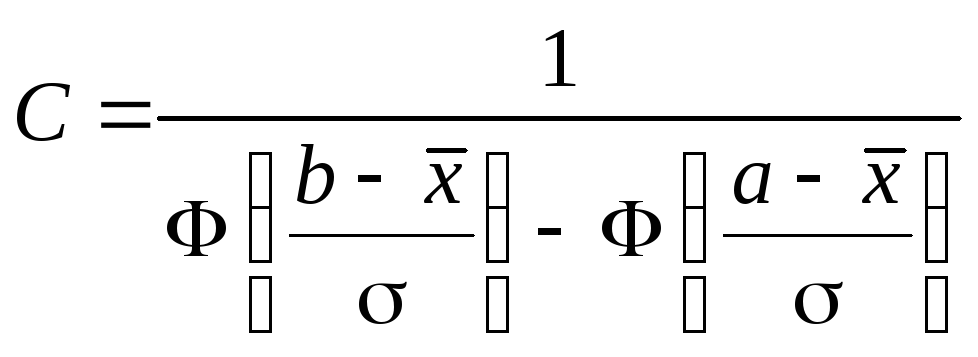 .
(1.40)
.
(1.40)
В
этих формулах
![]() и
относятся к основному распределению.
и
относятся к основному распределению.
В
частном случае для описания
распределения положительных
случайных величин (при х < 0, f(х)
= 0) формулы усеченного нормального
распределения при а
= 0 и
![]() имеют следующий вид:
имеют следующий вид:
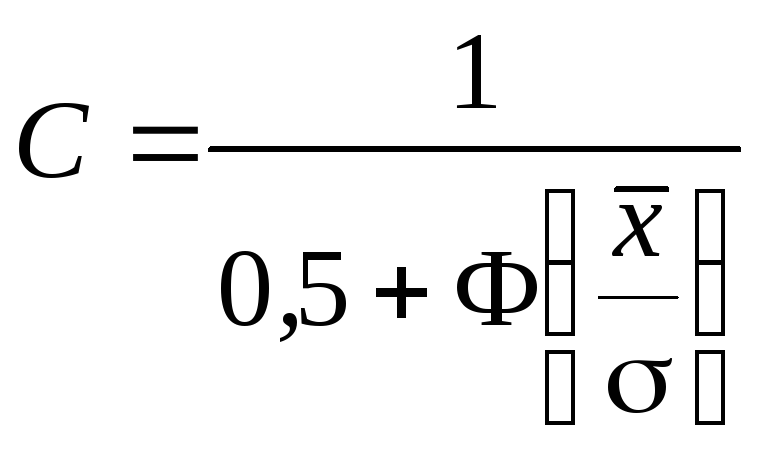 ;
(1.41)
;
(1.41)
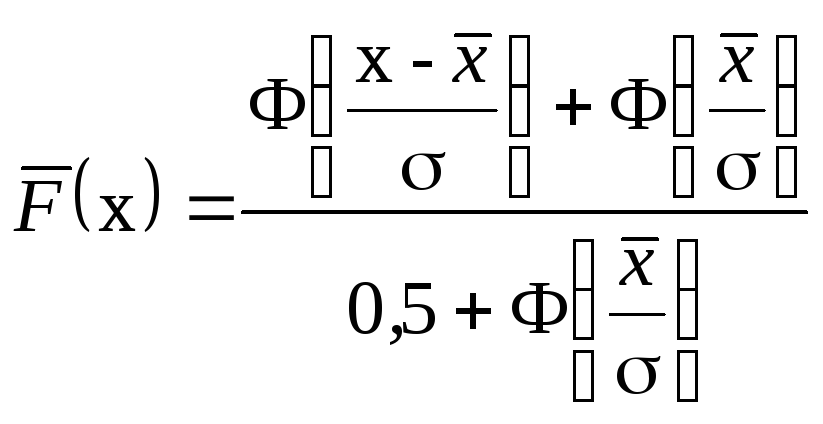 .
(1.42)
.
(1.42)
1.9.3. Экспоненциальное распределение
Экспоненциальное распределение характерно для внезапных отказов элементов и систем. Плотность вероятности экспоненциального распределения задается уравнением
![]() ,
,
![]() ,
,
![]() ,
x
> 0 ,
(1.43)
,
x
> 0 ,
(1.43)
где параметр распределения, являющийся строго положительной константой.
Среднее
значение
![]() и среднеквадратическое отклонение σ
экспоненциального распределения
совпадают и равны обратному значению
параметра
и среднеквадратическое отклонение σ
экспоненциального распределения
совпадают и равны обратному значению
параметра
![]() =
=![]() =
1/.
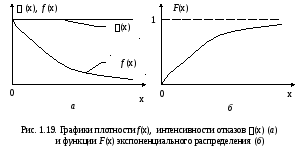
Графики функций
F(х)
и f(x)
приведены на рис. 1.19. Отличительной
особенностью экспоненциального
распределения является то, что
интенсивность отказов (х)
постоянна, т.e.
не зависит
от аргумента (значения случайной
величины).
=
1/.
Графики функций
F(х)
и f(x)
приведены на рис. 1.19. Отличительной
особенностью экспоненциального
распределения является то, что
интенсивность отказов (х)
постоянна, т.e.
не зависит
от аргумента (значения случайной
величины).
Основное свойство экспоненциального закона состоит в том, что при нем вероятность безотказной работы на данном интервале не зависит от времени предшествующей работы, а зависит от длины интервала. Это значит, что будущее поведение элемента не зависит от прошлого, если в данный момент он исправлен.
1.9.4. Распределение Эрланга
Это распределение при х > 0 задается следующими формулами:
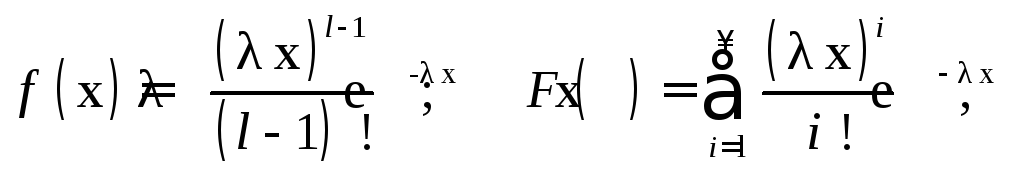 (1.44)
(1.44)
где и l – параметры распределения, причем параметр строго положителен, а l – целое положительное число.
Следует помнить, что частным случаем распределения Эрланга является экспоненциальное распределение (при l =1). Случайную величину X, имеющую распределение Эрланга с параметрами и l, можно интерпретировать как сумму взаимно независимых случайных величин X1, Х2, .., Хl, имеющих экспоненциальное распределение с параметром :
Х = Х1 + Х2 + ... + Хl. (1.45)
Среднее
значение
![]() и среднеквадратическое отклонение
распределения Эрланга определяются
по формулам:
и среднеквадратическое отклонение
распределения Эрланга определяются
по формулам:
![]() .
(1.46)
.
(1.46)
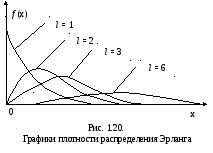
Графики плотности распределения f(х) при разных значениях l представлены на рис. 1.20. Интенсивность отказов (х) в данном случае монотонно возрастает.
![]() (1.47)
(1.47)
