Поверхности вращения

Если перемещение образующей линии представляет собой вращение вокруг некоторой неподвижной прямой (оси), то образованная в этом случае поверхность называется поверхностью вращения.

Образующая линия может быть плоской или пространственной кривой, а также прямой. Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости перпендикулярной оси вращения (рис. 42).

Эти окружности называются параллелями. Следовательно, плоскости, перпендикулярные оси, пересекают поверхность вращения по параллелям. Линия пересечения поверхности вращения плоскостью Σ, проходящей через ось, называется меридианом.

М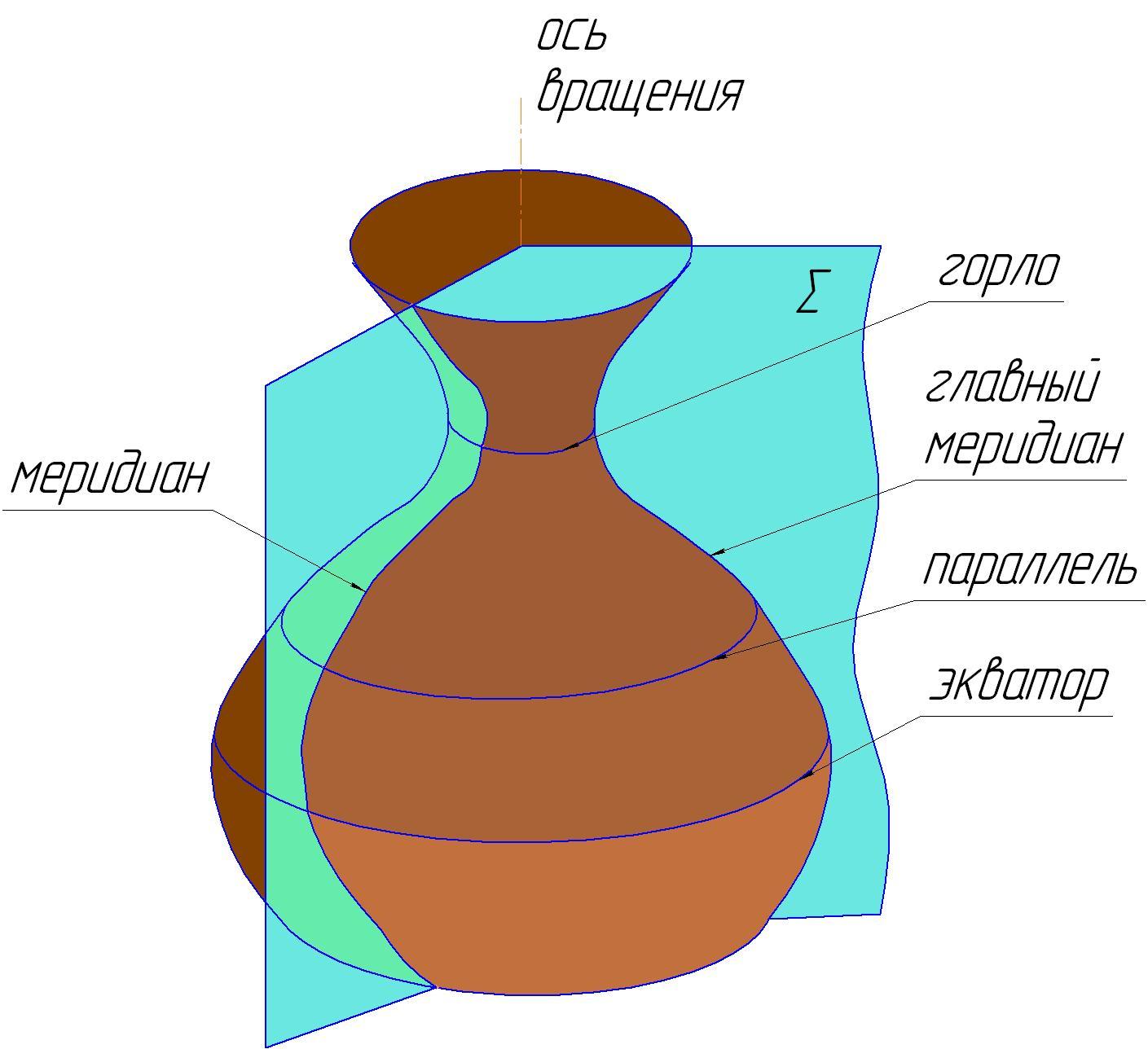еридиан, который является результатом пересечения поверхности вращения с плоскостью уровня, называетсяглавным. Проекция главного меридиана на плоскость, которой параллельна плоскость уровня, является очерковой линией соответствующей проекции поверхности вращения.

М

Рис. 42 Элементы поверхности вращения

37

ножество всех параллелей или меридианов представляет собой непрерывныйкаркас поверхности вращения. Через каждую точку поверхности проходит одна параллель и один меридиан. Проекции точки располагаются на соответствующих проекциях параллели или меридиана. Задать точку на поверхности или построить вторую проекцию точки, если одна задана, можно при помощи параллели или меридиана, которые проходят через эту точку.

При проектировании различных инженерных сооружений, машин и механизмов наибольшее распространение получили поверхности, образующиеся вращением прямой линии и кривых второго порядка.

Вращением прямой линии образуются:

– цилиндр вращения, если прямая l параллельна оси i (рис. 43 а);

– конус вращения, если прямая l пересекает ось i (рис. 43 б);

– однополостный гиперболоид, если прямая l скрещивается с осью i (рис. 43 в).

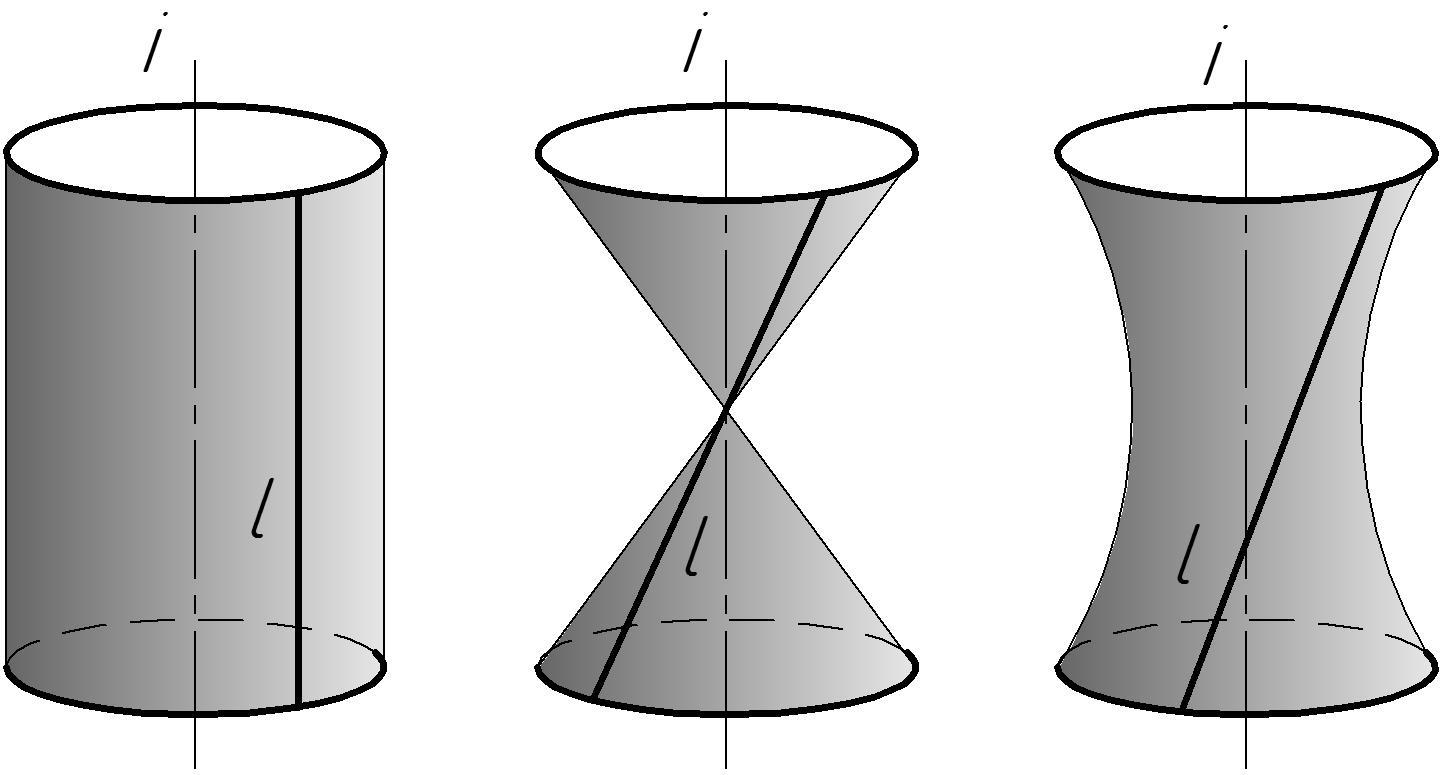
а	б	в
Рис. 43 Линейчатые поверхности вращения

К поверхностям вращения, образованным вращением кривых второго порядка вокруг оси относятся:

– сфера образуется вращением окружности вокруг ее диаметра (рис. 44 а);

– эллипсоид вращения образуется вращением эллипса вокруг большой или малой оси (44 б, в);

– тор образуется вращением окружности вокруг внешней оси (рис. 44 г);

а	б	в
г	д	е
Рис. 44 Поверхности вращения второго порядка

–

38

параболоид вращения образуется вращением параболы вокруг ее оси (рис. 44 д);

– однополостный гиперболоид вращения образуется вращением гиперболы вокруг ее мнимой оси. Эта поверхность образуется также вращением прямой (рис. 44 е).

Каналовые и циклические поверхности

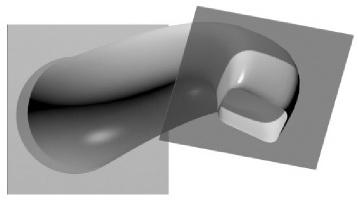
Каналовой называют поверхность, образованную непрерывным каркасом замкнутых плоских сечений, определенным образом ориентированных в пространстве. Площади этих сечений могут оставаться постоянными или монотонно изменяться в процессе перехода от одного сечения к другому. На рис. 45 приведены два изображения каналовой поверхности. В инженерной практике наибольшее распространение получили два способа ориентирования плоскостей образующих:

– параллельно какой-либо плоскости – каналовые поверхности с плоскостью параллелизма;

– перпендикулярно к направляющей линии – прямые каналовые поверхности.

Рис. 45 Каналовые поверхности

Каналовая поверхность может быть использована для создания переходных участков между двумя поверхностями типа трубопроводов, имеющих:

– различную форму, но одинаковую площадь нормального сечения;

– одинаковую форму, но различные площади сечения;

– различную форму и различные площади поперечных сечений.

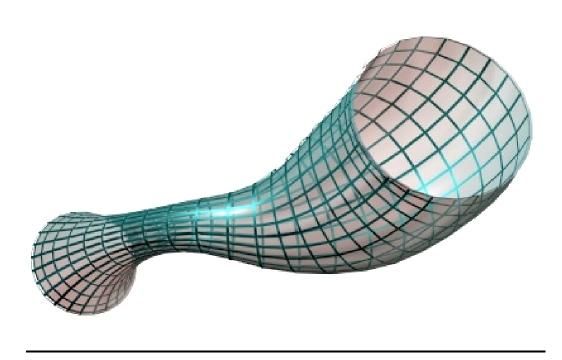
Циклическую поверхность можно рассматривать как частный случай каналовой поверхности. Она образуется с помощью окружности, центр которой перемещается по криволинейной направляющей. В процессе движения радиус окружности монотонно меняется. Пример циклической поверхности показан на рис. 46.

Т

39

рубчатая поверхность относится к группе нелинейчатых поверхностей с образующей постоянного вида и является частным случаем циклической и каналовой поверхностей. Она обладает свойствами, присущими этим видам поверхностей. У циклической поверхности она позаимствовала форму образующей, а у каналовой – закон движения этой образующей. На рис. 47 приведен пример трубчатой поверхности.

Рис. 46 Циклическая поверхность	Рис. 47 Трубчатая поверхность