Уравнения переноса энергии и массы
Пусть жидкость несжимаема, термо – и бародиффузия
отсутствует, const
D const
Выделим в смеси неподвижный параллелепипед с размерами
dx, dy, dz
При движении смеси вдоль оси x в выделенный параллелепипед за время d вносится масса i го компонента в количестве:
dM xi jxi dydzd
И вытекает: |
dM x dx,i |
jx dx,i dydzd |
После преобразований, аналогичных теплообмену, получим:
dmi |
|
2 |
|
( |
|
|
|
d |
D m |
|
6) |
|
|
|
|
|
i |
|
|
|
|
||
|
|
|
|
|
|
|
|
Уравнение (6) является дифференциальным уравнением |
|||||||
массообмена, |
описывающим распределение |
i го компонента |
|||||
массы |
|
|
|
|
|
||
в движущейся смеси, т.е. уравнение сохраненияi го компонента |
|||||||
массы |
vy |
vz |
0 |
|
|
|
|
Если vx |
и конвективная (молярная) диффузия |
||||||
отсутствует, тот уравнение массообмена примет вид: |
|
||||||
mi D 2 m |
В |
уравнении |
учитывается |
только |
|||
концентрационная диффузия. Это уравнение |
|||||||
|
|
i |
аналогично дифференциальному уравнению |
||||
|
|
|
теплопроводности |
при |
отсутствии |
||
|
|
|
внутренних источников теплоты. |
|
|||
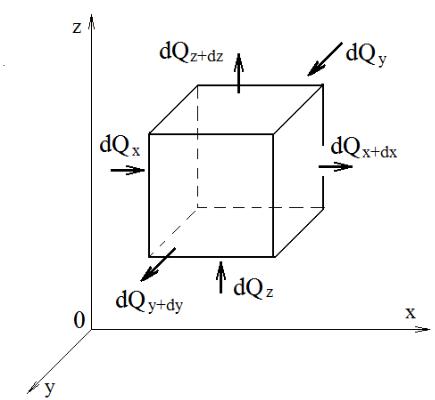
Далее рассмотрим уравнение энергии для смеси диффундирующих друг в друга компонентов. Примем, что внутренние источники теплоты отсутствуют, а физические параметры среды постоянны. Выделим на рис. неподвижный
параллелепипед с размерами
dx, dy, dz
и составим для него балансное уравнение энергии. Считаем, что подведенная теплота затрачивается только на изменение энтальпии выделенного параллелепипеда, а работа расширения равна нулю:
|
i |
|
|
|
|
divq |
|
|
|||
|
|
С другой стороны, плотность теплового потока с учетом конвективной диффузии:
q t jiii t vi jм.д.iii
Соответстве |
|
vxi jxiii |
|||||
qx t |
|
||||||
нно: |
|
|
|
|
|
|
|
|
|
|
x |
|
|
||
qy |
|
t |
|
vy i jyiii |
|||
y |
|||||||
|
|
|
|
||||
t
qz z vzi jziii
Проводим преобразования, аналогичные при рассмотрении теплообмена, получим уравнение энергии в виде:
|
dt |
|
|
|
|
|
|
|
|
|
|
сp |
2t ii divji |
ji |
gradii |
|
|||||||
d |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
ii divji |
2t |
ji gradii |
|
|
|
||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
И |
|
|
сp |
|
2t ji cpi |
t |
|||||
|
|
d |
|
||||||||
ли: |
|
|
|
|
|
|
|
|
|
||
Считая, что интенсивность термо – и бародиффузии мала, делаем вывод, что молекулярный перенос вещества осуществляется только концентрационной диффузией. Тогда:
ji D mi
Вывод: температурное поле смеси зависит от скорости vx , vy , vz и относительного массосодержания.
Молярная диффузия
Рассмотрим молярную диффузию или конвективный массообмен. Пусть требуется определить скорость испарения воды с поверхности водоема. Т.к. массообмен определяется конвективным процессом, то поток массы пропорционален разности между массовыми концентрациями на поверхности и в окружающей среде:
Jic F( ic i0 )
Или: |
jic ( ic |
i0 ) (mic mi0 ) |
(7) |
|
|||
где |
Jic поток массы, кг/с; |
|
|
jic |
плотность потока массы, кг/(м2∙с); |
коэффициент массоотдачи, отнесенный к разности концентраций диффундирующего вещества, м/с;
ic , i0 |
концентрация диффундирующего вещества у |
||
|
поверхности раздела фаз и вдали от нее, кг/ м3; |
||
mic , mi0 |
относительная |
массовая |
концентрация |
|
диффундирующего |
вещества |
соответственно у |
поверхности раздела фаз и вдали от нее.
Используя уравнение состояния идеальных газов, выражение (7)
запишем в виде: |
|
где |
p |
коэффициент массоотдачи, |
|
|
|
||||
jic p ( pic pi0 ) |
отнесенный |
к |
разности парциальных |
||
Коэффициенты |
давлений p pic pi 0 |
||||
|
и |
p |
связаны |
||
ассоотдачи |
соотношением |
||||
p RT
Тогда уравнение массоотдачи:
ji |
|
pic |
|
pi0 |
|
|
|
pic |
pi 0 |
|
|
|
|
||||||
|
|
RT |
RT |
||||||
RT |
|
||||||||
|
|
|
|
0 |
|
|
ср |
|
|
где |
R |
газовая постоянная диффундирующего газа, Д |
|
Tcр |
(кг∙К); температура пограничного слоя, |
|
T0 |
К; |
|
температура воздуха вдали от раздела фаз, К; |
|
|
T |
температура диффундирующего газа, К. |
Существует подобие процессов конвективного теплообмена и массообмена. По аналогии с числом Нуссельта используется
безразмерный |
комплекс, |
описывающий массообмен – число |
|||
Шервуда |
|
l0 |
l0 |
||
Sh |
Nu |
||||
|
|
Sh D |
|||
: |
|
|
|||
В |
литературе |
можно встретить вместо числа Шервуда другое |
||
|
|
|
|
NuD |
наименование этого комплекса – диффузионное число Нуссельта |
||||
По |
аналогии |
с числом Прандтля для теплообмена в теории |
||
|
|
|
|
Sс |
массообмена применяется число Шмидта |
||||
|
|
|
|
|
|
Pr |
|
Sc D |
|
|
a |
|
||
Число Шмидта характеризует отношение количества движения к массовой диффузии.
: Число Нуссельта является функцией чисел Рейнольдса и
Прандтля:
. Nu f (Re, Pr)
Учитывая подобие процессов конвективного тепло– и массообмена, можно предположить, что число Шервуда будет функцией чисел Рейнольдса иShШмидта:f (Re, Sc)
Если конвективный теплообмен описывается соотношением для расчета теплоотдачи от плоской пластины при ламинарном режиме обтекания: Nu 0,66 Re0,5 Pr
Соответствующее соотношение для ламинарного массообмена записывается: Sh 0,66 Re0,5 Sc0,33 Nu f (Gr, Pr)
Если массообмен осуществляется свободной конвекцией, то выражение для коэффициента массообмена можно получить из рассмотрения аналогичной задачи о теплообмене в условиях свободной конвекции. Как известно, теплообмен при свободной конвекции описывается соотношениями:
Gr |
g ' |
l3 |
|
|
g l3 (tС tЖ ) |
|||
0 |
0 |
|
0 |
|
||||
2 |
|
|
|
2 |
||||
|
|
|
|
|
||||
Для массообмена соответственно |
||||||||
получим: |
|
|
3 |
|
|
|
||
GrD |
|
g 'D |
l0 |
|
ic i0 |
|||
2 |
|
|
||||||
|
|
|
|
|
|
|||
Sh f (GrD , Sc)