Без вывода запишем закон косинусов Ламберта, который справедлив для черных тел и тел с диффузным излучением:

d 2Q E0 cos d dF

И для серого излучения закон Ламберта примет вид:

d 2Q E0 cos d dF

и для спектрального излучения:

dE E cos d

Однако многие тела не подчиняются этому закону. Например, полированные металлы имеют яркость излучения при

60 80

превышающую яркость в направлении нормали к поверхности. При увеличении

60 80 яркость уменьшается до нуля.

Если для данного тела известна зависимости яркости интегрального или спектрального излучения, то в общем случае поверхностная плотность собственного излучения определяется из соотношений:

/ 2

E 2 I ( )sin cos d

0

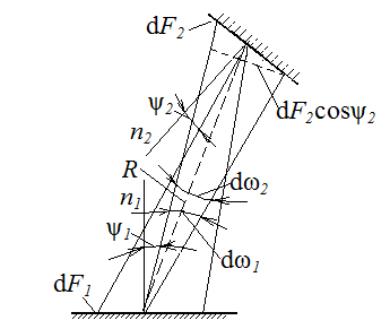
Радиационный теплообмен между твердыми телами

Чтобы получить распределение в пространстве излучения тела конечного размера и произвольной формы, необходимо просуммировать энергию излучения в соответствующих направлениях всех элементарных площадок, составляющих поверхность данного тела.

При исследованиях лучистого теплообмена между телами, разделенными прозрачной (диатермичной) средой, используются различные методы – метод многократных отражений, метод натянутых нитей (нити Хоттеля), метод

эффективных тепловых потоков, метод сальдо).

Остановимся на методе, основанном на последовательном учете многократных затухающих отражений и поглощений (метод Нуссельта). Остальные рассмотрим при решении задач.

не зависят от температуры и координат точек на поверхностях,

вдоль поверхностей не меняются. Определим плотность потока результирующего излучения.

Собственное излучение первого тела: EC E1

Это собственное излучение первой поверхности полностью попадает на вторую поверхность и поглощается в количестве:

E1 A2

Остальная часть отражается второй поверхностью обратно в направлении

И т.д. Аналогично такую процедуру можно выполнить и для второй поверхности.

Для расчета результирующего потока можно использовать выражение:

Метод наглядный, но наиболее громоздкий. Другие методы (метод эффективных тепловых потоков, метод сальдо) рассмотрим на практике.

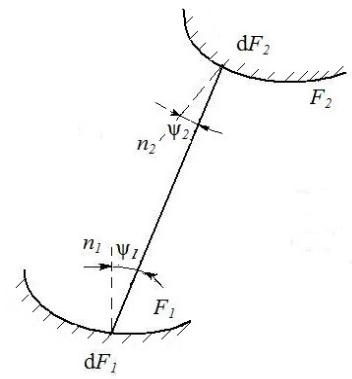
Рассмотрим два тела, разделенных диатермичной средой, причем одно тело находится в полости другого. Тело 1 –выпуклое, а тело 2 – вогнутое.

характеризуетизл чениячасть. потока эффективного излучения, который попадает со второго тела на первое по отношению к полному потоку

эффективного излучения второго тела. Угловой коэффициент1

12

, т.к. энергия, излучаемая первым телом, полностью попадает на второе тело. Угловой коэффициент 11 0

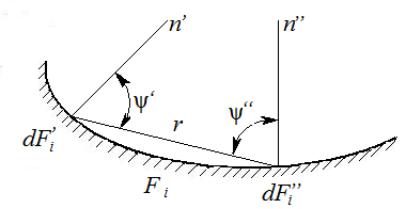
Рассмотрим теплообмен между вогнуто F1 и выпуклой F2 поверхностями

Угловой коэффициент диффузного излучения какой-то поверхности на другую является только геометрическим фактором, определяемый формой поверхностей, их размерами, взаимным расположением и расстоянием между ними.

Поток эффективного излучения поверхности Fсаму на себя можно записать в виде

1

(плотность потока эффективного излучения по поверхности принимается постоянной):

Угловой коэффициент зависит от геометрических особенностей:

–для собственного диффузного излучения тела при одинаковой плотности этого излучения по всей поверхности и одинаковой температуре;

–для отраженного диффузного излучения при одинаковой плотности потока этого излучения по всей его поверхности.

Угловые коэффициенты излучения определяются различными методами – интегрирования, поточной алгебры, натянутых нитей Хоттеля, интегрирования по контуру, дифференцирования известных угловых коэффициентов, сферы единичного радиуса Нуссельта. Также используются графические и экспериментальные методы. В результате применения этих методов получен ряд формул для многих случаев взаимного расположения тел.

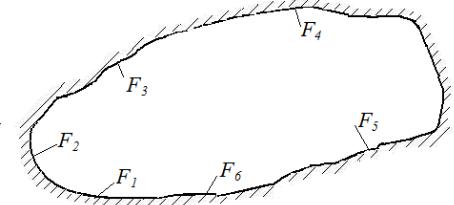
Свойство 3. Если между одним из тел замкнутой системы происходит радиационный теплообмен со всеми другими телами, то сумма угловых коэффициентов переноса энергии излучения этого тела на все тела, образующие замкнутую систему, равна 1, а сумма всех взаимных поверхностей тел равна поверхности этого тела (рис.). Общий поток излученияF1поверх, можностипредставить в виде:

Q1 E1 F1 E1 F1 11 E1 F1 12 ... E1 F1 1n

Отсюда получаем: F1 F1 11 F1 12 ... F1 1n