1. Степень свободы. Кинематические связи

Количественная оценка кинематических свойств системы основана на определении ее степеней свободы как направлений возможных независимых перемещений. Число степеней свободы (W) – это минимальное число независимых параметров, необходимых для определения положения всех точек системы. Такими параметрами могут быть перемещения отдельных точек, углы поворота элементов и др.

Число степеней свободы простых систем можно определять путем задания ее элементам возможных перемещений (рис. 2.2 а, б, в).

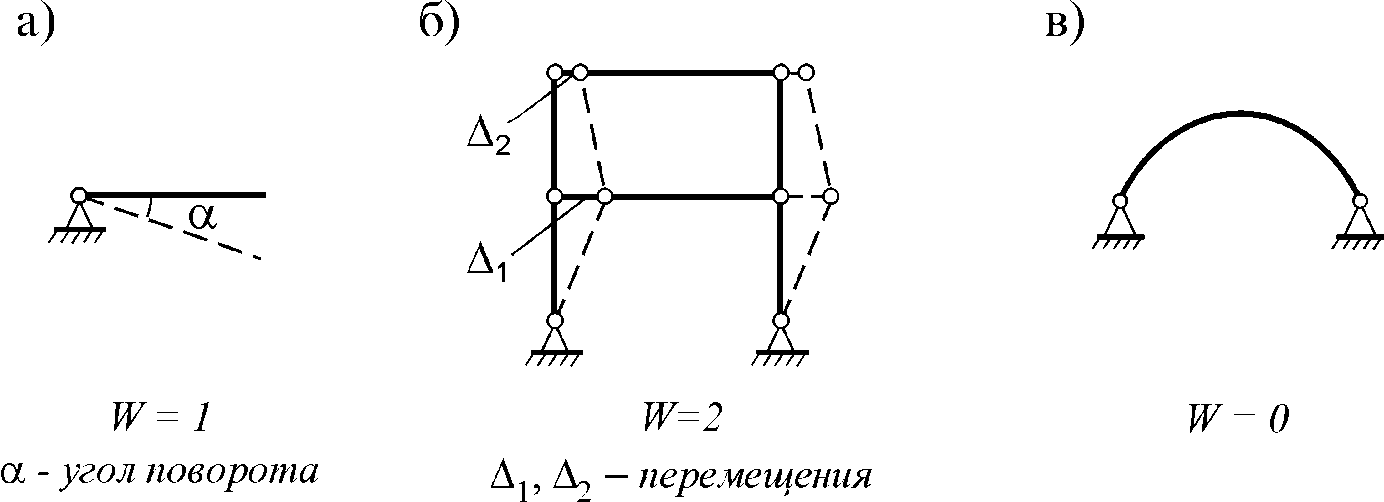
Рис. 2.2

Для изучения более сложных случаев введем следующие понятия:

диск (Д) – неизменяемая часть системы, состоящая из одного или нескольких жестко связанных элементов (рис. 2.3 а);

шарнир (Ш) – связь, дающая возможность взаимного поворота соседним дискам (рис. 2.3 б);

припайка (П) – связь, жестко закрепляющая соседние диски (рис. 2.3 в);

стержень (С) – связь, ограничивающая перемещение диска в одном направлении (рис. 2.3 г);

опорная связь (С₀) – связь, ограничивающая перемещение диска в одном направлении по отношению к земле (рис. 2.3 д).

Рис. 2.3

Определим число степеней свободы точки (рис. 2.4 а) и диска с различными кинематическими связями (рис. 2.4 б-д):

Рис. 2.4

Как видим, стержень или опорная связь уменьшают число степеней свободы на единицу, шарниры – на два, припайки – на три.

Кинематические связи должны обеспечивать неподвижность системы относительно земли (основания), а также неизменяемость ее внутренней структуры. Если при удалении одной связи из неизменяемой системы она становится изменяемой, то эта связь называется необходимой. Если после этого система остается неизменяемой, то связь называется избыточной. Связь, соединяющая систему с землей, называется внешней, а находящаяся внутри – внутренней связью.

Шарнир, объединяющий два диска, называется простым шарниром (рис. 2.5 а). Если шарнир объединяет несколько дисков, то он называется кратным шарниром. Кратный шарнир эквивалентен нескольким простым шарнирам. Кратность шарнира определяется по формуле n_Ш=n_Д –1, где n_Д – число дисков, объединяемых шарниром.

Рис. 2.5

2. Число степеней свободы стержневой системы

Рассматривая расчетную схему сооружения как систему дисков, объединенных связями, получаем ее дисковый аналог. Для одной и той же системы часто можно получить несколько дисковых аналогов.

Число степеней свободы плоской стержневой системы определяется по формуле, называемой основной формулой кинематического анализа:

W = 3n_Д – 2n_Ш – n_C – – 3n_П .

Здесь n_Д – число дисков в дисковом аналоге; n_Ш – число простых шарниров; n_С – число стержней; – число опорных связей; n_П – число припаек.

При расчете фермы можно использовать формулу

W = 2n_У – n_C – ,

где n_У – число узлов фермы (узлом считается любой шарнир, связывающий стержни фермы).

После расчета по этим формулам возможны три случая:

1) W>0 – такая система геометрически изменяема и является механизмом;

2) W=0 – в системе имеется достаточное число связей; если они введены правильно, то система неизменяема и статически определима;

3) W<0 – в системе есть избыточные связи. Если эти связи введены правильно, то система неизменяема и статически определима.

Отсюда следует, что расчетная схема сооружения должна удовлетворять необходимому условию геометрической неизменяемости

W 0.

В качестве примера рассмотрим три расчетные схемы (рис. 2.6 а, в, д) и их дисковые аналоги (рис. 2.6  б, г, е, ж).

Рис. 2.6

Вычислим число степеней свободы этих систем:

1) арка (рис. 2.6 а): n_Д=2, n_Ш=1, n_C=0, =4, n_П=0;

W=32 – 21 – 0 – 4 –30 =0;

2) рама (рис. 2.6 в): n_Д=3, n_Ш=3, n_C=0, =3, n_П=0;

W=33 – 23 – 0 – 3 –30 =0.

3) ферма (рис. 2.6 д):

– по дисковому аналогу (рис. 2.6 е): n_Д=6, n_Ш=7, n_C=0, =4, n_П=0;

W = 36 – 27 – 0 – 4 –30 = 0;

– по дисковому аналогу (рис. 2.6 ж): n_Д=2, n_Ш=1, n_C=1, =3, n_П=0;

W = 32 – 21 – 1 – 3 –30 = 0;

– по формуле для фермы (рис. 2.6 д): n_У=4, n_С=5, 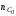=3;

W = 24 – 5 – 3 = 0.