
- •19. Определение коэффициента гидравлического трения по длине. Виды местных сопротивлений. Расчетные формулы.
- •20. Истечение жидкости и газа через малое отверстие в тонкой стенке. Траектория вытекающей струи.
- •21. Истечение жидкости и газа через большие отверстия. Истечение при переменном уровне. Опорожнение сосудов.
- •22. Насадки. Истечение жидкости через насадки при постоянном напоре. Вакуум в насадках. Определение вакуума.
- •23. Движение жидкости по трубам. Простой трубопровод. Расчетные формулы. Сложные трубопроводы.
- •24. Расчет трубопроводов с последовательным и параллельным соединением труб. Расчет трубопроводов с путевым расходом. Расчет разветвленной и кольцевой сети.
19. Определение коэффициента гидравлического трения по длине. Виды местных сопротивлений. Расчетные формулы.

Рассмотрим
два соседних слоя движущейся жидкости
и элементарный участок площадью dS.
Относительная скорость движения слоёв
 ,
скорость поперечного движения частиц
жидкости из одного слоя в другой -
,
скорость поперечного движения частиц
жидкости из одного слоя в другой -
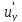 (рис.).
Из одного слоя в другой в единицу времени
переходит масса жидкости
ρ
(рис.).
Из одного слоя в другой в единицу времени
переходит масса жидкости
ρ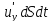 ,
изменение
количества движения или импульс силы
dTdt=ρ
,
изменение
количества движения или импульс силы
dTdt=ρ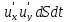 ;
;
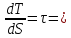 ρ
ρ (1) - касательное
напряжение при турбулентном режиме
движения.
(1) - касательное
напряжение при турбулентном режиме
движения.
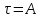 ρ
ρ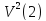 ,
где А – безразмерный коэффициент,
зависящий от шероховатости поверхности.
,
где А – безразмерный коэффициент,
зависящий от шероховатости поверхности.
По
основному уравнению равномерного
движения:
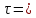 ρgRI,
где R
– гидравлический радиус - отношение
площади затопленного сечения трубопровода
или канала, через которое протекает
жидкость, т.е. живого сечения потока, к
смоченному периметру, R=
ρgRI,
где R
– гидравлический радиус - отношение
площади затопленного сечения трубопровода
или канала, через которое протекает
жидкость, т.е. живого сечения потока, к
смоченному периметру, R=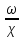 ;
;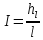 – гидравлический уклон – изменение
полного напора по длине участка.
– гидравлический уклон – изменение
полного напора по длине участка.

Из
решения:
 (3) -
формула
Шези, С=
(3) -
формула
Шези, С=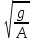 -скоростной
множитель
или коэффициент
Шези;
получим
-скоростной
множитель
или коэффициент
Шези;
получим
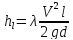 (5)
– формула
Дарси-Вейсбаха,
где λ=
(5)
– формула
Дарси-Вейсбаха,
где λ=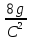 ,
,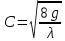 ;
Потери
по длине зависят от шероховатости
стенок.
;
Потери
по длине зависят от шероховатости
стенок.
 -
абсолютная шероховатость,
-
абсолютная шероховатость,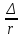 -относительная шероховатость,
-относительная шероховатость,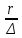 - относительная гладкость,
- относительная гладкость,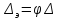 - гидравлически эквивалентная
шероховатость.
- гидравлически эквивалентная
шероховатость.
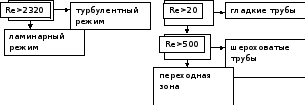
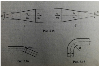
Основные зоны при движении жидкости по трубам различной шероховатости.
ламинарный режим
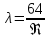 ;
;линейная зона
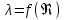 ;
;переходная или доквадратичная зона
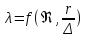 ;
;квадратичная автомодельная область или область шероховатых труб
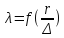 .
.
 Местные
сопротивления в трубах
–
сопротивления в устройствах, в которых
происходит резкая деформация потока,
выражающаяся в изменении скорости или
направления движения.
Местные
сопротивления в трубах
–
сопротивления в устройствах, в которых
происходит резкая деформация потока,
выражающаяся в изменении скорости или
направления движения.
Общая
формула для вычисления местных
сопротивлений:

Виды местных сопротивлений:
1)потери при изменении сечения потока (вход/выход; внезапное расширение/сужение; плавное расширение/сужение);
 ;
;
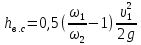 или
или
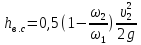 ;
;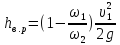 или
или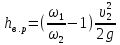 ,
где
,
где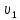 и
и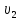 - скорости до и после расширения
соответственно;
- скорости до и после расширения
соответственно;
Диффузор – плавное
расширение потока ξ=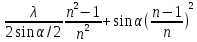 ,
где
,
где ,
,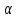 - угол конусности.
- угол конусности.
Конфузор – плавное
сужение потока ξ=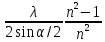
РИС.3.15
2)потери при изменении направления потока (колена; повороты и т.д.);
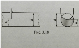
При резком повороте
ξ=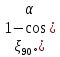 ,при
плавном поворотеξ=
,при
плавном поворотеξ=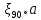 ,где
,где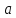 - табличный коэффициент, зависящий от
радиуса закругления,
- табличный коэффициент, зависящий от
радиуса закругления,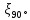 =(0,2+0,001
=(0,2+0,001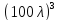 )
)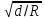 РИС.3.16
и 3.17
РИС.3.16
и 3.17
3)потери при протекании через арматуру различного типа (вентили; клапаны и т.д.);
ξ
=f(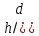 ;
ξ=
;
ξ=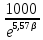 ,где
,где
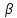 =
=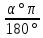 РИС.3.18
РИС.3.18
4)потери при делении или слиянии потока.
 ,
,
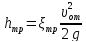 ;
;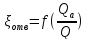 ,
,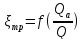 .
.
20. Истечение жидкости и газа через малое отверстие в тонкой стенке. Траектория вытекающей струи.
Малое отверстие– отверстие, вертикальный размер которого значительно (в 5-10 раз) меньше глубины погружения отверстия под уровень жидкости в сосуде, через который проистекает жидкость.
Тонкая стенка – стенка, в которой
вытекающая струя соприкасается лишь с
кромкой отверстия, обращённой внутрь,
и не касается боковой поверхности
отверстия, т.е. толщина стенки 2-2,5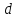 .
.
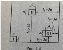
На расстоянии, близком к
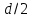 ,
происходит поперечное сжатие струйки,
,
происходит поперечное сжатие струйки,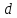 уменьшается, так что
уменьшается, так что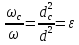 –коэффициент
сжатия трубы.
–коэффициент
сжатия трубы.
Сжатие: 1)неполное, 2) совершенное полное, 3) несовершенное полное. РИС. 4.4
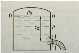
Закон Бернулли для сечений 0-0 и 1-1 при истечении из резервуара в атмосферу:
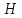 +
+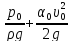 =
=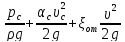 ,
,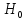 =
=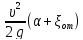
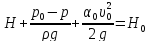 - напор истечения,
- напор истечения,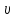 =
=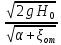 ,φ=
,φ=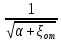 - коэффициент скорости.
- коэффициент скорости.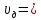 φ
φ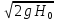 ,
для идеальной
жидкости
,
для идеальной
жидкости
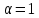 ,
,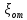 =0,
тогда
=0,
тогда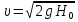 -формула
Торичелли, φ=
-формула
Торичелли, φ=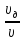 .
.
Расход: Q=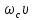 =μ
=μ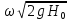 ,
,
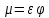 –коэффициент
расхода.
–коэффициент
расхода.
Для малого отверстия
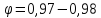 ,μ=0,62,
,μ=0,62,
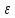 =0,64.
H=
=0,64.
H=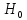
Истечение под
уровень:
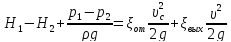
 H+
H+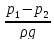 =
=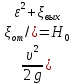
Траектория вытекающей струи.
Инверсия–изменение
формы сечения струи в зависимости от
формы отверстия. В вертикальной плоскости
x=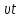 ,
y=
,
y=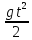 ,
,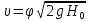 ;
;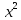 =4
=4 .
.
