
1-6_na_pechat
.docxМеханика жидкостей и газа
-
Основные физические свойства жидкости и газа. Параметры, определяющие свойства жидкостей и газов. Силы, действующие на жидкость.
Жидкость – физ. тело, обладающее большим сопротивлением изменению своего объема и малым сопротивлением изменению своей формы. Ж. отличаются от твердых тел малой силой сцепления между частицами и их легкоподвижностью, благодаря чему ж. принимает форму сосуда, в который она налита. Это свойство - текучесть. Ж. бывают: капельными – несжимаемыми (вода, нефть) и газообразными – сжимаемыми. (пары, газы).
Физические свойства:
-
Плотность:
 .
Для дистиллированной воды при
.
Для дистиллированной воды при


-
Удельный вес – вес жидкости на единицу объема:
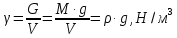 .
.
-
Относительная плотность (относительный удельный вес) – отношение плотности (уд. веса) ж. к плотности (удельному весу) ж. при
 :
:

-
Сжимаемость - способность ж. уменьшать объем при увеличении давления.
Коэффициент
объемного сжатия
– относительное изменение объема
жидкости при единичном изменении
давления:
 .
.

Объемный
модуль упругости
– величина, обратная
 :
:
 .
.

-
Температурное расширение – способность ж. изменять объем при изменении температуры.
Коэффициент
температурного расширения
– относительное изменение объема ж.
при изменении температуры на
 :
:
 .
.
 .
.
-
Вязкость – св-во жидкости оказывать сопротивление перемещению ее частиц и развивать при движении внутренние касательные напряжения:
 ,
,
где
 - сила внутр. трения, Н; S
– площадь трущихся слоев, м2;
- сила внутр. трения, Н; S
– площадь трущихся слоев, м2;
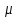 – динамическая
вязкость жидкости, [Па∙с]
= [10 П] – пуаз.
– динамическая
вязкость жидкости, [Па∙с]
= [10 П] – пуаз.
τ
- касательное напряжение: (для ньютоновских ж.) и
(для ньютоновских ж.) и
 (для неньютоновских ж.),
(для неньютоновских ж.),
 - касательное напряжение покоящейся
жидкости.
- касательное напряжение покоящейся
жидкости.
Динамическая вязкость численно равна единичной силе трения (τ) при градиенте скорости равном единице. Знак ± говорит, что два соседних слоя взаимодействуют: слой с большей скоростью ускоряет другой (+), слой с меньшей скоростью – тормозит (-).
Кинематическая
вязкость
– отношение µ к плотности жидкости:
 .
.
du/dy – градиент скорости, характеризующий отн. изменение скорости du между отдельными слоями толщиной dy, с-1. du/dy = tg β, где β – угол наклона касательной к эпюре.
Рисунок 1. Эпюра скоростей

Вязкость обычной (ньютоновской) ж. зависит от рода ж. и температуры. Прибор для определения вязкости ж. – вискозиметр. Для неньютоновских ж. вязкость зависит от градиента скорости (строительные растворы, нефтепродукты).
Силы, действующие на жидкость
-
Поверхностные силы (силы гидродинамического давления, силы упругости, трения) распределены по поверхности ж. и пропорциональны ее площади:
 ,
где
p
– единичная сила или напряжение, Н/м2;
ω
– площадь действия силы, м2.
,
где
p
– единичная сила или напряжение, Н/м2;
ω
– площадь действия силы, м2.
-
Массовые (объемные) силы (силы тяжести, инерции, центробежная сила) действуют на все частицы данного объема ж. и пропорциональны массе (объему – для однородных ж.) жидкости:
 ,
где
,
где
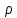 - плотность ж., кг/м3;
а
– ускорение, м/с2;
W
– объем ж., м3.
- плотность ж., кг/м3;
а
– ускорение, м/с2;
W
– объем ж., м3.
-
Силы поверхностного натяжения обуславливаются силами сцепления молекул поверхностного слоя, который стремятся уменьшить свободную поверхность ж.:
 ,
где
σ
– коэффициент поверхностного натяжения,
Н/м; l
– периметр действия силы.
,
где
σ
– коэффициент поверхностного натяжения,
Н/м; l
– периметр действия силы.
По отношению к какому-либо объему силы можно разделить на внешние (действующие со стороны окружающей среды) и внутренние (поверхностные силы взаимодействия частиц ж.).
-
Гидростатическое давление и его свойства.
Гидростатическое
давление –
предел отношения элементарной силы,
действующей на элементарную площадку
dS
при dS→0:
 ,
Па.
,
Па.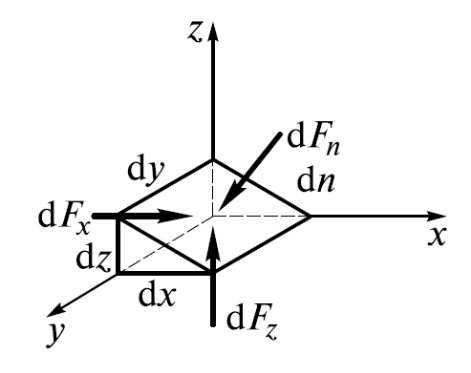
Свойства гидростатического давления:
1. ГД всегда направлено по внутренней нормали к поверхности, на которую оно действует, и создает только сжимающее напряжение.
2. ГД в точке ж. не зависит от ориентации площадки в пространстве и будет одинаковым по всем направлениям: рх = рz = рn.
Если давление Р отсчитывают от абсолютного нуля, то его называют абсолютным давлением Рабс. Если давление отсчитывают от атмосферного, то оно называется избыточным (манометрическим) Ризб. Оно измеряется манометром. Атмосферное давление постоянно Ратм = 100 кПа. Вакуумметрическое давление Рвак - недостаток давления до атмосферного.
-
Дифференциальные уравнения равновесия жидкости.

Выделим
в покоящейся ж. элементарный объем.
Заменим влияние окр. ж. силами
гидростатического давления
(по ОХ это p∙dy∙dz
и (p+ )dy∙dz).
На параллелепипед действует и массовая
сила,
проекции кот. равны:
)dy∙dz).
На параллелепипед действует и массовая
сила,
проекции кот. равны: ,
где
,
где - проекции ускорений массовой силы на
оси; ρ-плотность
ж.
- проекции ускорений массовой силы на
оси; ρ-плотность
ж.
Суммируя
проекции этих сил на ОХ, получим ур-е
равновесия на OX:


Преобразуем
и, выведя ур-я аналогично для ОY
и OZ,
получим систему
ДУ
равновесия
ж. Эйлера.![]()
Умножим
каждое уравнение на
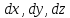 соответственно и сложим. Выражение в
скобках – полный дифференциал dp.
соответственно и сложим. Выражение в
скобках – полный дифференциал dp.
![]()
Преобразуем и получим основное ДУ гидростатики.
Представим его в виде: dp=ρ∙dП, где П - силовая функция (функция потенциала сил). Капельная ж. может находиться в равновесии только под действием сил, имеющих потенциал.
Из
основного ДУ гидростатики при р=const,
ρ=const,
dp
= 0 получим
уравнение
поверхности равного давления
(поверхности,
давление во всех точках которой
одинаково).![]()
-
Равновесие жидкости под действием силы тяжести. Основное уравнение гидростатики. Закон Паскаля.

Рассмотрим
покоящуюся жидкость, когда на нее
действует только сила тяжести:
 ,
z
– вертикальная отметка точки. ДУ
гидростатики принимает вид:
dp
= -ρgdz.
Проинтегрируем
и получим:
,
z
– вертикальная отметка точки. ДУ
гидростатики принимает вид:
dp
= -ρgdz.
Проинтегрируем
и получим:![]()

Первая форма основного уравнения гидростатики:
Вторая
форма основного уравнения гидростатики:
 )
)
Давление в точке 2 выше давления в вышележащей точке 1 на величину произведения удельного веса на разность отметок высот этих точек.
Основное
уравнение гидростатики:
 ),
),
где –
избыточное (манометрическое) давление.
–
избыточное (манометрическое) давление.
Полное (абсолютное) давление в любой точке жидкости складывается из давления на свободную поверхность и давления, созданного весом вышележащего слоя жидкости (столбом).
Закон Паскаля: внешнее давление на жидкость в замкнутом сосуде (давление на свободную поверхность) передается внутри жидкости во все точки без изменений.
-
Пьезометрическая высота. Гидростатический напор.

Под действием абсолютного давления в сосуде жидкость в трубках поднимается на разные высоты.
hпр = Paбс/ ρg – приведенная высота абсолютного давления;
hп = (Pабс - Paтм) / ρg = Pизб / ρg – приведенная высота избыточного давления (пьезометрическая высота)
Приведенная высота абс давления больше пьезометрической высоты на величину приведенной высоты атмосферного давления: hпр - hп = Pатм / ρg.
Рассмотрим
резервуар относительно горизонтальной
плоскости 0-0. 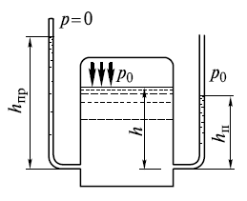
 –
пьезометрический
напор,
равный сумме высоты положения точки
отн. 0-0 и пьезометрической высоты.
–
пьезометрический
напор,
равный сумме высоты положения точки
отн. 0-0 и пьезометрической высоты.
НS = Pизб / ρg + Paтм/ ρg + zA = Paбс/ ρg + zA - гидростатический напор, равный сумме высоты положения точки относительно 0-0 и приведенной высоты абсолютного давления.
Прибор,
измеряющий абсолютное давление в точке
присоединения, – жидкостный манометр,
открытая сверху трубка, измеряющая
избыточное давление – пьезометр.
-
Равновесие газа в поле силы тяжести. Относительный покой жидкости и газа.
Уравнение
равновесия для несжимаемых жидкостей
можно использовать и для ![]()
газов. Однако для несжимаемых ж. ρ=Const, а в случае газа ρ – величина переменная.
Изменение состояния газа может происходить различными способами. Рассмотрим 3 случая:
-
Однородная атмосфера: ρ= Const
Распределение
давления газа по высоте:
 ,
где
ро
–
давление в точке с координатой zo.
,
где
ро
–
давление в точке с координатой zo.
-
Изотермическая: P/ρ= gRT=Const, где R –унив. газ. постоянная, Т – t
 воздуха на высоте H:
воздуха на высоте H:
Распределение давления по высоте при равновесии газа при изотермических условиях:
 – высота
изотермической атмосферы.
– высота
изотермической атмосферы.
-
Политропная: P/ρn = Pо/ρоn =Const
Изменение
давления по высоте политропной атмосферы:

Изменение
температуры по высоте политропной
атмосферы:

Температура
воздуха убывает по направлению снизу
вверх по линейному закону, уменьшаясь
на 1 на каждые 100 м высоты политропной
атмосферы.
на каждые 100 м высоты политропной
атмосферы.
Относительный покой – случай, когда ж. движется, но относительно движущейся вместе с ней системы координат она может рассматриваться неподвижной.
Случай
1. Прямолинейное
равноускоренное движение сосуда с ж.:
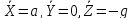

Давление
в любой точке жидкости плотностью ρ,
находящейся в сосуде, движущемся с
постоянным ускорением а:

Уравнение поверхности равного давления: p= Const =C1= ax+ gz.
Угол ее наклона tg= - a/g
 Случай
2. Цилиндрический сосуд с ж., вращающийся
вокруг вертикальной оси с
постоянной угловой скоростью:
Случай
2. Цилиндрический сосуд с ж., вращающийся
вокруг вертикальной оси с
постоянной угловой скоростью:

Давление
в любой точке ж.:

Уравнение
поверхности равного давления:
 (представляет собой параболоид вращения).
(представляет собой параболоид вращения).
