1.1Исходные данные

Исходными данными для выполнения работы являются :

измеренные, правые по ходу, горизонтальные углы (графа 2.табл. № 1,приложение 2);

горизонтальные проложения сторон (графа 2.табл. № 1, приложение 2) – эти данные для всех вариантов одинаковы.

Значения координат «х» и «у» первой вершины и дирекционного угла стороны 1-2 индивидуальны и, в зависимости от варианта, берутся по таблице № 1 приложения 1; заносятся в табл. № 1 в графы : 4, 12, 13, в строчки, отмеченные звездочками.

1.2 Вычисление координат вершин замкнутого теодолитного хода

Уравнивание измеренных углов

Измерения горизонтальных углов сопровождаются неизбежными ошибками (невязками).

Угловая невязка вычисляется по формуле:

Σ β изм = β1 + β 2+ … + βn - сумма измеренных горизонтальных углов,

Σ β теор - теоретическая сумма внутренних углов замкнутого

Если полученная невязка не превышает допустимую, то ее разбрасывают с обратным знаком на все измеренные углы, не дробя при этом менее чем на 0,1'.

Вписывают полученные поправки (δ β ) над значениями углов (графа 2 таблицы 2). С учетом поправок и их знака вычисляют исправленные углы:

5

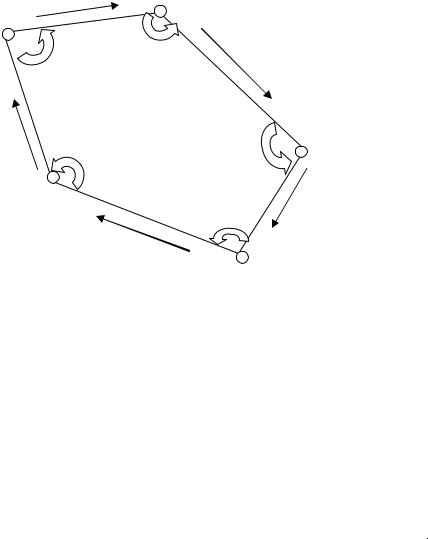
Пример: для построения плана был проложен замкнутый теодолитный ход в виде пятиугольника (рис. 1), в котором были измерены правые по ходу горизонтальные углы. Результаты измерений приведены в табл. 1.

Б

А

В

Д

Г

Рис. 1. Замкнутый теодолитный ход Точки А, Б, В, Г, Д – станции замкнутого теодолитного хода и

вершины горизонтальных правых по ходу углов. Стрелками показано направление хода.

Таблица 1. Результаты измерения и исправления горизонтальных углов

Теоретическую сумму внутренних углов пятиугольника (которым является наш замкнутый теодолитный ход) вычисляем согласно формулы 2: 180°(5 – 2) = 540°.

Определяем угловую невязку: 539° 58.3' - 540° = - 1,7'.

6

Вычисляем допустимую невязку: ± 1,5' 5 = ± 3,35'

Т. к. полученная невязка меньше допустимой по абсолютной величине, распределяем ее на все измеренные углы с обратным знаком, т. е. с плюсом; причем к большим углам прибавим большие поправки.

Проверяем сумму исправленных углов, она равна 540°.

Вычисление дирекционных углов сторон теодолитного хода

Дирекционный угол (α ) – это угол, отсчитываемый от северного направления осевого меридиана до рассматриваемой стороны по ходу часовой стрелки. Он изменяется от 0˚ до 360˚.

Вычисление дирекционных углов сторон теодолитного хода выполняют по формуле:

где α n-1 - дирекционный угол предыдущей стороны, α n- дирекционный угол последующей стороны,

β прав.испр. – правый исправленный угол между рассматриваемыми сторонами.

Вычисление дирекционных углов ведется в столбик, при этом следует помнить, что в одном градусе – 60 минут.

Контролем верного вычисления дирекционных углов служит равенство заданного дирекционного угла и вычисленного начальной стороны теодолитного хода.

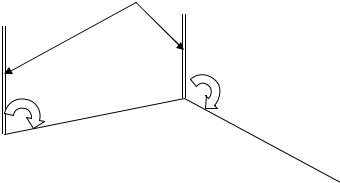
Осевые меридианы

В

Рис. 2. Схема дирекционных углов сторон АБ и БВ

7

Пример: дирекционный угол стороны А-Б равен : 79° 58'.

Дирекционный угол стороны Б-В : 79° 58' + 180° - 113° 49,5' = 146° 08,5' Дирекционный угол стороны В-Г: 146° 08,5' + 180° - 101° 05,5' = 225° 03' Дирекционный угол стороны Г-Д: 225° 03' + 180° - 98° 17,7' = 306° 45,3' Дирекционный угол стороны Д-А: 306° 45,3' + 180° - 150° 35,7' = 336° 9,6' Дирекционный угол стороны А-Б: 336° 09,6' + 180° - 76° 11,6' = 439° 58'.

Если значения вычисленных дирекционных углов больше 360°, перед занесением результатов в таблицу, вычитаем 360°.

Например: дирекционный угол стороны А-Б: 439° 58' - 360° = 79° 58'.

Определение румбов и знаков приращений координат

Румб – это острый угол, отсчитываемый от ближайшего окончания осевого меридиана до ориентируемой линии.

Вычисление румбов осуществляется в зависимости от того, в какой четверти геодезических прямоугольных координат находится ориентируемая линия.

Таблица 2. Значения румбов

Знаки приращений координат определяются также по положению рассматриваемой стороны, т.е. в зависимости от того, в какой четверти геодезических прямоугольных координат находится конкретная сторона теодолитного хода.

Пользуясь таблицей 2 или рисунком 3, определить значения румбов, их название относительно сторон света, знаки приращений координат; результаты занести в соответствующие графы таблицы 1 Приложения 2.

Например: Дирекционный угол стороны Б-В : 146° 08,5', следовательно она находится во второй четверти.