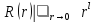- •V(X) потенциалдық өрісте қозғалатын бөлшектің іргелі операторларының уақыт бойынша толық туындысы:е)
- •Орталық симметриялы өрісте r(r) радиалды функция үшін Шредингердіңрадиалды теңдеуі:
- •Сызықтық гармоникалық оператордың импульстік көріністегі толқындық функциясы: ,
- •Сызықтық гармоникалықоператордың импульстік көріністегі толқындық функциясы:
- •Гейзенбергтің анықталмағандық принципі тек қана мына щамалармен сипатталады:а)
- •Кванттық механикадағы коммутатор:а)
- •Сызықты гармоникалық осцилляторды кванттау шарттары: а)
- •Сызықты гармоникалық осцилятордың уақытқа тәуелділігі .:а)
- •Сызықтық гармоникалық осциллятордың толқындық функциясының асимптотикасы былай жазылады:
- •Тік бұрышты бір өлшемді шұңқырда Электрон негізгі күйде орналасқан . Бұл күйдегі импульстің орташа мәні : а)
Тік бұрышты бір өлшемді шұңқырда Электрон негізгі күйде орналасқан . Бұл күйдегі импульстің орташа мәні : а)
Тік
бұрышты потенциалды тосқауылға энергиясы
Е бөлшектер ағыны түседі : V(x) = 0, егер x
< 0 (I) и V(x) = 0, егер x≥0 (II). Толқындық
сандар k1
және k2
I және II обылыста анықталған .Бір өлшемді
теңдеудің шешімдері :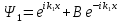 и
и
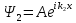 .
Амплитудалары A және B:
А)
.
Амплитудалары A және B:
А)
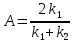 ,
В)
,
В)
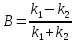
Тік
бұрышты потенциалды тосқауылға энергиясы
Е бөлшектер ағыны түседі.
Тосқауыл кеңістікті
 және
және
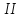 ,
обылыстарға бөледі, импульстерінің
белгіленуі
,
обылыстарға бөледі, импульстерінің
белгіленуі
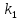 және
және
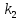 .
Бөлшектің тосқауылдан шағылу ықтималдылығы
:
А)
.
Бөлшектің тосқауылдан шағылу ықтималдылығы
:
А)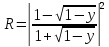 ,
өлшемі жоқ параметр
,
өлшемі жоқ параметр
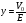 В)
В)
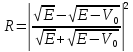 С)
С)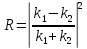
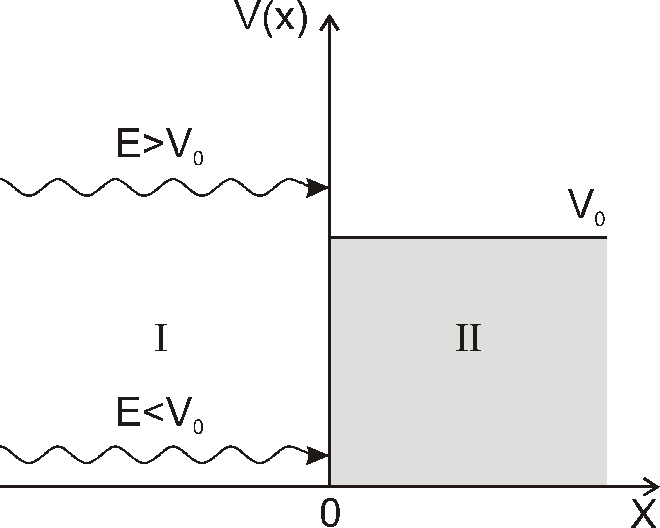
Тік
бұрышты потенциалды тосқауылға энергиясы
Е бөлшектер ағыны түседі.
Тосқауыл
кеңістікті Ι
және ΙΙ,
обылыстарға бөледі, импульстерінің
белгіленуі k_1 және k_2. Бөлшектің
тосқауылдан шағылу ықтималдылығы
А)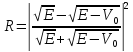 В)
В)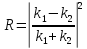
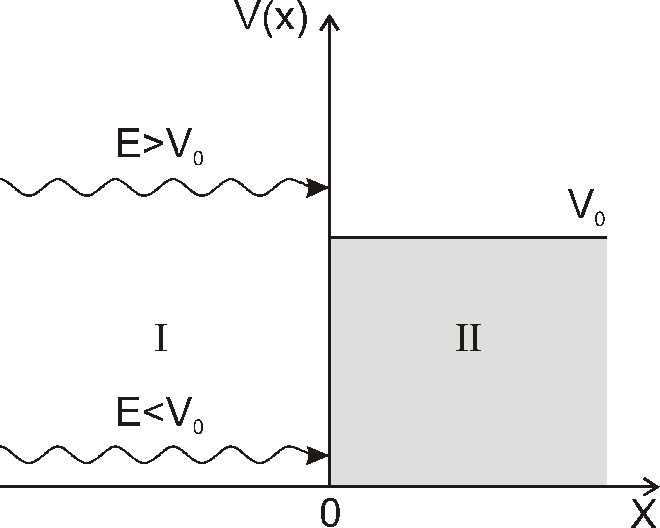
Тік
бұрышты потенциалды тосқауылға энергиясы
Е бөлшектер ағыны түседі.: V(x)=0, егер x<0
и V(x)=0, егер x≥0. Толқындық сандар k1 және
k2 I және II обылыста анықталған . Бір текті
теңдеудің шешімін көрсет.
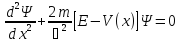 :
А)
:
А)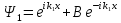 I облыс В)
I облыс В)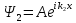 облыс II
облыс II
Тік
бұрышты потенциалды тосқауылға энергиясы
Е бөлшектер ағыны түседі.: V(x)=0, егер x<0
и V(x)=0, егер x≥0. Толқындық сандар k1 және
k2 I және II обылыста анықталған. Бір текті
теңдеудің шешімдері: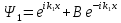 и
и
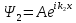 .
A және B амплитудаларын көрсет: А)
.
A және B амплитудаларын көрсет: А)
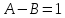 В)
В)
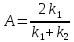 С)
С)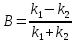
Тік
бұрышты потенциалды тосқауылға энергиясы
Е бөлшектер ағыны түседі.: V(x)=0, егер x<0
и V(x)=0, егер x≥0. Толқындық сандар k1 және
k2 I және II обылыста анықталған.
Бір текті теңдеудің шешімдері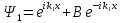 и
и
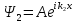 толқын жиынтығын береді: А)
толқын жиынтығын береді: А)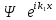 – түскен толқын ,
– түскен толқын ,
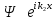 – өткен толқын В)
– өткен толқын В)
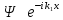 – шағылған толқын
– шағылған толқын
Тік
бұрышты шексіз терең және ені
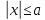 шектелген потенциальды шұңқыр үшін
Шредингер теңдеуі:
А)
шектелген потенциальды шұңқыр үшін
Шредингер теңдеуі:
А)
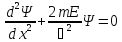
Уақыт
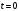 мезетінде бөлшек гармоникалық
осциллятордың 2-ші қоздырылған күйінде
орналасқан:
мезетінде бөлшек гармоникалық
осциллятордың 2-ші қоздырылған күйінде
орналасқан:
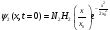 ,
мұнда
,
мұнда
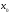 – осциллятордың параметрі. Толқындық
функция
– осциллятордың параметрі. Толқындық
функция
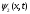 кез-келген уақыт мезетінде былай
жазылады:а)
кез-келген уақыт мезетінде былай
жазылады:а)
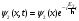 б)
б)
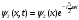 с)
с)
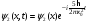
Уақыт
бойынша
квантты-механикалы
шамаларды
дифференциалдау
шарттары
:А)
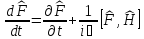
Уақыт
бойынша
квантты-механикалы
шамаларды
дифференциалдау
шарттары
:А)
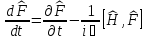 ,
В)
,
В)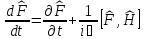
Уақыт
бойынша
операторлар
көбейтіндісін дифференциалдау
шарттары
:
А)
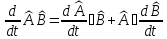
Уақыт
бойынша
операторлар
көбейтіндісін дифференциалдау
шарттары:
А) ,
В)
,
В)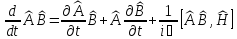
Уақыт
бойынша операторлардың көбейтіндісінің
дифференциалы:а)
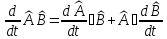 б)
б)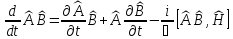 с)
с)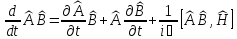
Үздіксіз
спектрдің толқындық функциясының
нормировка жасалу шарты:
А)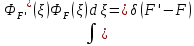
Үш
өлшемді гармоникалық осцилляторды
кванттау шарттары: А)

Шексіз
қабырғалары бар потенциалды шұңқырдағы
бөлшектің энергетикалық деңгейлерінің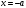 және
және
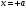 ,
нүктелердегі квантталу шарты: А)
,
нүктелердегі квантталу шарты: А)
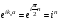 ,
где
,
где
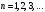 В)
В)
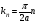 ,
где
,
где
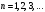 С)
С)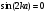
Шредингер теңдеуіне кіретін толқындық функция арқылы анықтауға болады:А) Кеңістіктің кез-келген нүктесінде бөлшектің табылу ықтималдылығын. В) физикалық шаманың орташа мәнін, С) Ықтималдылық тығыздығын
Шредингер
теңдеуінің шешімдері, егер сыртқы
қобалжудың потенциалын
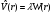 Гамильтон операторы үшін ескерсек
Гамильтон операторы үшін ескерсек
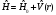 :
А) Спектральды сызықтардың дублетті,
триплетті және т.б. бөлінуін ескерсек.
В) Орталық-симметриялы өрістегі азғындалу
жайлы гипотезаны ескерсек
:
А) Спектральды сызықтардың дублетті,
триплетті және т.б. бөлінуін ескерсек.
В) Орталық-симметриялы өрістегі азғындалу
жайлы гипотезаны ескерсек
Шредингер
теңдеуінің шешімдері, егер сыртқы
қобалжудың потенциалын
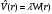 Гамильтон операторы үшін ескерсек
Гамильтон операторы үшін ескерсек
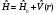 :
А) Спектральды
сызықтардың дублетті, триплетті және
т.б. бөлінуін ескерсек, В) Орталық-симметриялы
өрістегі азғындалу жайлы гипотезаны
ескерсек, С)Берілген жағдайындағы
:
А) Спектральды
сызықтардың дублетті, триплетті және
т.б. бөлінуін ескерсек, В) Орталық-симметриялы
өрістегі азғындалу жайлы гипотезаны
ескерсек, С)Берілген жағдайындағы
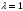 қобалжу
теориясы әдісімен анықталады.
қобалжу
теориясы әдісімен анықталады.
Шредингердің
стационар теңдеуі келтірілген түрі:
А)
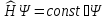
Шредингердің
стационар теңдеуі:
А)
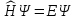
Шредингердің
стационар теңдеуінің уақытқа тәуелділігі
(еркін бөлшек үшін): А)
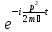
Шредингердің
толқындық функциясын көрсет: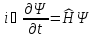
Шредингердің
уақыт бойынша толық теңдеуі былай
жазылады:
А)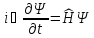
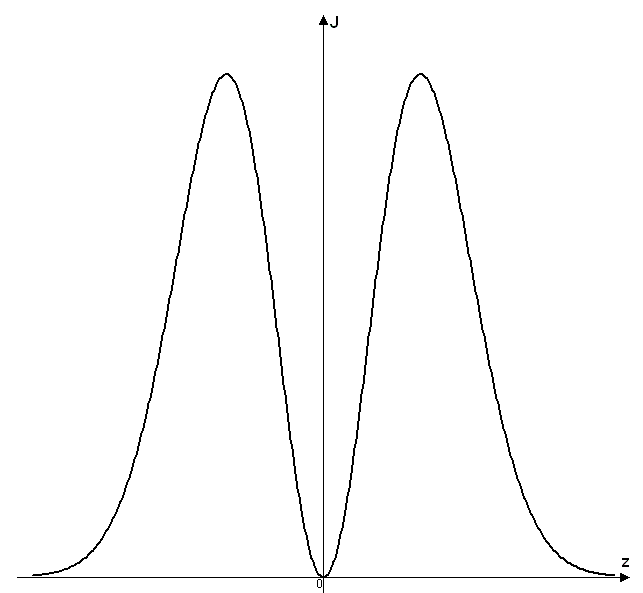
Штерна-Герлах
тәжірибесі электронның спинін анықтау
үшін қойылған еді. Тәжірибеде алынған
нәтижелер суретте көрсетілген. Мынадай
қорытынды жасауға болады: А) электрон
– фермион және оның спині z осіне
параллель, немесе антипараллель болады.
Электрон
мына күйде орналасқан
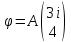 .
Нормалай
тұрақтысы А
мынаған
тең:А)
.
Нормалай
тұрақтысы А
мынаған
тең:А)
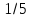
Электронның металлдан шығу суық эмиссиясы былай түсіндіріледі: А) туннель эффектісімен
Энергетикалық
деңгейлердің сыртқы электр өрісінің
әсерінен ығысуын Штарк
эффекті деп
атайды. Біртекті электр өрісіндегі
сызықты гармоникалық осциллятор үшін
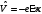 :
А) сызықтық эффект жоқ, яғни
:
А) сызықтық эффект жоқ, яғни
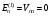 В) Штарктың квадратты эффекті байқалады,
С Барлық деңгейлер
В) Штарктың квадратты эффекті байқалады,
С Барлық деңгейлер
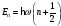 ығысқан
ығысқан
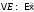 төмен ығысқан.
төмен ығысқан.
Эрмит
полиномы үшін
рекуррентті
формулалар:
А)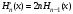 В)
В)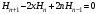 ,
С)
,
С)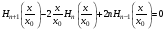
Эрмит
полиномын
анықта: А)
Родригес формуласынан
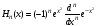 В)
Эрмит
теңдеуінен
В)
Эрмит
теңдеуінен
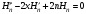 С) Рекуррентті
қатынастан
С) Рекуррентті
қатынастан
Эрмит
полиномының қасиеттері:А)
Ортонормировкалы
болуы
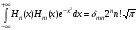 .
В) жұптылық
.
В) жұптылық
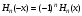
Эрмитті
оператордың матрицалық элементтерінің
қасиеттері :А) Диагональ
элементтері
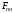 – тек нақты сандар В)
– тек нақты сандар В)
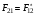 ,
,
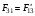 и т.д.
и т.д.
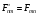
Эрмитті
операторларға
мысалдар: А)
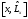 ,В)
,В)
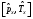 ,
С)
,
С)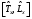
Эрмитті
операторларға мысалдар:А)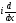 .В)
.В)
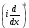 ,
кез-келген k мәнінде, С)
,
кез-келген k мәнінде, С)
 ,
кез-келген k мәнінде
,
кез-келген k мәнінде
Эрмитті
операторлардың матрицалық элементтерінің
қасиеттері:А)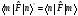 .
В) диагоналды
элементтері
.
В) диагоналды
элементтері
 – тек
нақты сандар, С)
– тек
нақты сандар, С)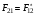 ,
,
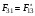 және
т.б.
және
т.б.
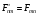
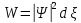 мағынасы
бар
мағынасы
бар
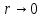 жағдайда
орталық-симметриялы өрістегі радиал
толқындық функцияны көрсет
жағдайда
орталық-симметриялы өрістегі радиал
толқындық функцияны көрсет
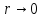 , А)
, А)