
- •V(X) потенциалдық өрісте қозғалатын бөлшектің іргелі операторларының уақыт бойынша толық туындысы:е)
- •Орталық симметриялы өрісте r(r) радиалды функция үшін Шредингердіңрадиалды теңдеуі:
- •Сызықтық гармоникалық оператордың импульстік көріністегі толқындық функциясы: ,
- •Сызықтық гармоникалықоператордың импульстік көріністегі толқындық функциясы:
- •Гейзенбергтің анықталмағандық принципі тек қана мына щамалармен сипатталады:а)
- •Кванттық механикадағы коммутатор:а)
- •Сызықты гармоникалық осцилляторды кванттау шарттары: а)
- •Сызықты гармоникалық осцилятордың уақытқа тәуелділігі .:а)
- •Сызықтық гармоникалық осциллятордың толқындық функциясының асимптотикасы былай жазылады:
- •Тік бұрышты бір өлшемді шұңқырда Электрон негізгі күйде орналасқан . Бұл күйдегі импульстің орташа мәні : а)
Сызықты гармоникалық осцилляторды кванттау шарттары: а)
Сызықты
гармоникалық
осциллятордың
потенциалы:
А)
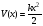 ,
мұнда
серпімділік коэффициенті
,
мұнда
серпімділік коэффициенті
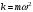 В)
В)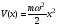
Сызықты
гармоникалық осциллятор үшін Шредингер
теңдеуінің Эквивалентті
жазылуы–
координаталы
және
өлшемсіз
(айнымалылар
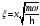 и
и
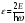 ):
А)
):
А)
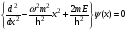 В)
В)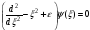
Сызықты
гармоникалық осциллятор үшін Шредингер
теңдеуінің Эквивалентті
жазылуы өлшемсіз
(айнымалылар
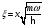 ):
):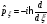 и
и
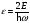 :
А)
:
А)
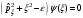 ,
В)
,
В)
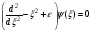 С)
С)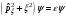
Сызықты
гармоникалық осцилятор үшін толқындық
функцияны дифференциялдасақ,онда
өлшемсіз айнымалыда
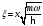 :
а)
:
а)
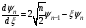 б)
б)
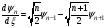
Сызықты
гармоникалық осцилятордың толқындық
функциясы үшін рекуррентті қатынастар
орындалады
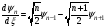 және
және
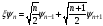 мынадай дифференциалдық қатынас дұрыс:
А)
мынадай дифференциалдық қатынас дұрыс:
А)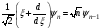 В)
В)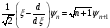
Сызықты гармоникалық осцилятордың уақытқа тәуелділігі .:а)
Сызықтық
гармоникалық осциллятордың алгебралық
өрнектелудегі моделі жоюшы операторға
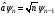 (төмендететін) және туғызатын операторға
(төмендететін) және туғызатын операторға
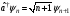 (жоғарылататын) сүйенеді, ол операторлар
мынадай өлшемсіз айнымалылармен
сипатталады
(жоғарылататын) сүйенеді, ол операторлар
мынадай өлшемсіз айнымалылармен
сипатталады
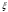 және
және
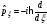 :
А)
:
А)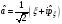 ,
В)
,
В)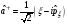
Сызықтық
гармоникалық осциллятордың алгебралық
өрнектелудегі моделі жоюшы операторға
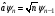 (төмендететін) және туғызатын операторға
(төмендететін) және туғызатын операторға
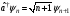 (жоғарылататын) сүйенеді, ол операторлар
мынадай өлшемсіз айнымалылармен
сипатталады
(жоғарылататын) сүйенеді, ол операторлар
мынадай өлшемсіз айнымалылармен
сипатталады
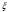 және
және
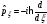 :
А)
:
А)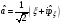 ,
В)
,
В)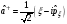 ,
С)
,
С) 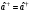
Сызықтық
гармоникалық осциллятордың негізінде
жоятын оператор
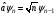 (төмендететін) және пайда болатын
(төмендететін) және пайда болатын
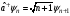 (жоғарылататын) операторлар бар. Олардың
өлшемі жоқ айнымалы арқылы мына түрде
жазылады
(жоғарылататын) операторлар бар. Олардың
өлшемі жоқ айнымалы арқылы мына түрде
жазылады
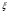 :а)
:а)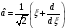 б)
б)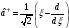
Сызықтық
гармоникалық осциллятордың негізінде
жоятын оператор (төмендететін) және
пайда болатын (жоғарылататын) операторлар
бар, олардың өрнектелуі:а)
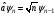 б)
б)
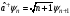
Сызықтық
гармоникалық осциллятордың негізінде
жоятын оператор (төмендететін) және
пайда болатын (жоғарылататын) операторлар
бар,олар үшін мына қатынас орындалады:а)
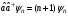 б)
б)
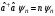
Сызықтық
гармоникалық осциллятордың орташа
кинетикалық энергиясы
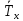 : А)
: А)
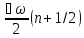
Сызықтық
гармоникалық осциллятордың орташа мәні
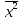 берілген
берілген
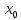 өлшем бірлігінде:
А)
өлшем бірлігінде:
А)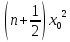
Сызықтық
гармоникалық осциллятордың орташа мәні
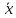 берілген
берілген
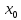 өлшем
бірлігінде:А)
0
өлшем
бірлігінде:А)
0
Сызықтық гармоникалық осциллятордың толқындық функциясының асимптотикасы былай жазылады:
Сызықтық
операторлардың анықтамасы және
қасиеттері:А)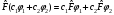 – анықтамасы, В) егер операторлар
– анықтамасы, В) егер операторлар
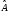 және
және
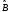 сызықты болса, онда оператор
сызықты болса, онда оператор
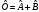 сызықты болады С)егер операторлар
сызықты болады С)егер операторлар
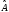 және
және
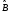 сызықты болса, онда оператор
сызықты болса, онда оператор
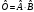 әрдайым сызықты болады
әрдайым сызықты болады
Табиғаттағы барлық бөлшектер екі топқа бөлінеді – фермиондар, бозондар. Осыған байланысты мынадай заңды байқаймыз: а)Барлық белгілі адрондар – фермиондар б) Барлық белгілі мезондар – бозондар
Табиғаттағы барлық бөлшектер екі топқа бөлінеді – фермиондар, бозондар. Осыған байланысты мынадай заңды байқаймыз: а) Барлық белгілі адрондар – фермиондар б) Барлық белгілі мезондар – бозондар с) Симметрия қасиеті екі бөлшектің орын ауыстыруына байланысты бөлшектердің тобына байланысты болады
Тепе-тең
бөлшектердің ажыратылмас шарты:
А)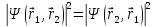
Толқындық
функцияның нормировка жасау шарты
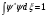 :
А) энергияның сақталу заңымен теңестіруге
болады, В) Уақыт бойынша нормировканың
сақталу заңын көрсетеді
:
А) энергияның сақталу заңымен теңестіруге
болады, В) Уақыт бойынша нормировканың
сақталу заңын көрсетеді
Толқындық
Функцияның квадратының өлшемі
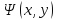 :
: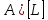 -1
-1
Туылу
және жойылу операторлары үшін коммутациалық
қатынастар
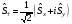 және
және
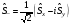 :
А)
:
А)
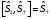 В)
В)
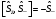
Туылу
және жойылу операторлары үшін коммутациалық
қатынастар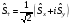 және
және
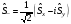 :А)
:А)
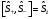 В)
В)
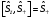 В)
В)
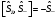
Туылу
және жою операторлары
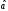 және
және
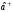 сызықты гармоникалық осциллятор
моделінде мына қатынастарды
қанағаттандырады: А)
сызықты гармоникалық осциллятор
моделінде мына қатынастарды
қанағаттандырады: А)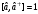 ,
В)
,
В)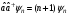 ,
С)
,
С)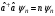
Туылу
және жою операторлары
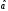 және
және
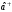 сызықты гармоникалық осциллятор
моделінде мына қатынастарды
қанағаттандырады:
А)
сызықты гармоникалық осциллятор
моделінде мына қатынастарды
қанағаттандырады:
А)
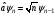 , В)
, В)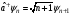 ,
С)
,
С)
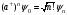
Тік бұрышты бір өлшемді шексіз потенциальды шұңқырда толқындық функцияның 2 түйіні бар. Бұл күйде кванттық сан п қандай мән қабылдайды:а) 3
