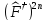- •V(X) потенциалдық өрісте қозғалатын бөлшектің іргелі операторларының уақыт бойынша толық туындысы:е)
- •Орталық симметриялы өрісте r(r) радиалды функция үшін Шредингердіңрадиалды теңдеуі:
- •Сызықтық гармоникалық оператордың импульстік көріністегі толқындық функциясы: ,
- •Сызықтық гармоникалықоператордың импульстік көріністегі толқындық функциясы:
- •Гейзенбергтің анықталмағандық принципі тек қана мына щамалармен сипатталады:а)
- •Кванттық механикадағы коммутатор:а)
- •Сызықты гармоникалық осцилляторды кванттау шарттары: а)
- •Сызықты гармоникалық осцилятордың уақытқа тәуелділігі .:а)
- •Сызықтық гармоникалық осциллятордың толқындық функциясының асимптотикасы былай жазылады:
- •Тік бұрышты бір өлшемді шұңқырда Электрон негізгі күйде орналасқан . Бұл күйдегі импульстің орташа мәні : а)
Кванттық механикадағы коммутатор:а)
Кванттық
механикадағы өлшенетін шамалар – бұл
орташа шамалар
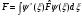 .
Базисті функцияның сипатталуында,
мысалы оператор
.
Базисті функцияның сипатталуында,
мысалы оператор
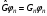 ,
матрицалық элементтің комбинациясы
арқылы өрнектеледі
,
матрицалық элементтің комбинациясы
арқылы өрнектеледі
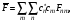 где:
а)
где:
а)
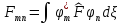 б)
б)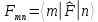 с)
с)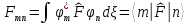
Кванттық механикадағы суперпозиция принципі:А)Микробөлшектің корпускулалы-толқындық дуализмін көрсетеді, В) Кванттық-механиканың операторларын тек қана сызықты етіп көрсетеді, С) Динамикалық теңдеулердің тек қана сызықтық болуын талап етеді
Кванттық
механикадағы үздіксіздік теңдеуі
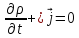 (
(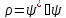 – ықтималдылық тығыздығы,
– ықтималдылық тығыздығы,
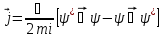 – ықтималдылық тогының тығыздығы)
сақталу заңын көрсетеді:
А) ықтималдылықты, В) Бөлшектер санын
– ықтималдылық тогының тығыздығы)
сақталу заңын көрсетеді:
А) ықтималдылықты, В) Бөлшектер санын
Кванттық
механикадағы үздіксіздік теңдеуі
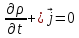 (
( – ықтималдылық тығыздығы,
– ықтималдылық тығыздығы,
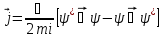 – ықтималдылық тогының тығыздығы)
сақталу заңын көрсетеді: А)
массаның сақталу заңын,
– ықтималдылық тогының тығыздығы)
сақталу заңын көрсетеді: А)
массаның сақталу заңын,
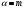 ,
В) зарядтың сақталу заңын,
,
В) зарядтың сақталу заңын,
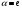 ,
С) бөлшектің сақталу заңын ,
,
С) бөлшектің сақталу заңын ,
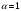
Кванттық механиканың кейбір әдістері жуықтау әдіске жатады: А) Хартри-Фок әдісі В) Вариациялық әдіс С)Қоздыру теориясы
Кванттық механиканың келесі жуықтау әдістері белгілі: А) Вариациялық әдіс В) Қоздыру теориясы
Кванттық-механикалық жүйе жалпы жағдайда қандай тәуелділерге байланысты болады: ξ - жалпыланған координата, t – уақыттың параметрі
Квантық
механикалық шама қозғалыс интегралы
болады, егер:А)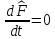 В)
В)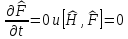 С)
Уақыт бойынша толық туынды нөлге тең
С)
Уақыт бойынша толық туынды нөлге тең
Кез келген берілген оператор мына жағдайда өзгермейді: А)Екі рет комплексті түйіндес болған да В) Екі рет транспортировка жасаған да двойном
Кез
келген үш сызықты оператор Якоби
теңдігіне қанағаттандырады:
![]() А)
А)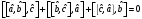 В)
В) С)
С)
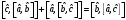
Кейбір
біртекті потенциальдардың энергетикалық
спектрлерінің
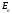 квантталу шарты:
А)
квантталу шарты:
А)
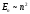 – симметриялы тік бұрышты шұңқыр
– симметриялы тік бұрышты шұңқыр
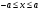 шексіз ұзын қабырғалары бар. В)
шексіз ұзын қабырғалары бар. В)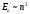 симметриясыз тік бұрышты шұңқыр
симметриясыз тік бұрышты шұңқыр
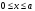 шексіз ұзын қабырғалары бар, С)
шексіз ұзын қабырғалары бар, С)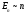 – сызықты гармоникалық осциллятор
– сызықты гармоникалық осциллятор
Кейбір жағдайда ғана орындалмайтын дәл шешімі бар модельді есептер: А) Ангармоникалық осциллятор , В)Вудс-Саксон потенциалы С) Бір текті электр өрісінде қозғалатын бөлшек
Кейбір
жағдайлардан басқа операторлардың
сызықтық болу шарты:
А)Комплексті түйіндес:
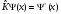 В)
квадратты түбірден шығару :
В)
квадратты түбірден шығару :
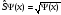 С) логарифмдеу
С) логарифмдеу
Кейбір
іргелі коммутаторлардан уақыт бойынша
алынған толық туынды: А)
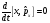 ,
В)
,
В)
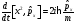 С)
С)
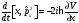
Келесі
жұп операторларында ортақ меншікті
функциялар жүйесі жоқ:
А)
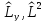
Келесі операциялар кез-келген оператордың түрін өзгертпейді:А)Екі рет комплексті түйіндес болуы, В)Екі рет транспонировка жасалуы, С)Екі рет эрмитті түйіндес болуы
Коммутатор
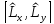 тең:А)
тең:А)
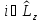
Коммутатор
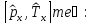 А)
0
А)
0
Коммутатор
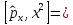 ,
егер
Якоби
теңдігі орындалса
,
егер
Якоби
теңдігі орындалса
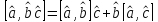 А)
А)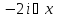
Коммутатор
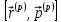 :
импульс
арқылы өрнектелуі:
А)
:
импульс
арқылы өрнектелуі:
А) 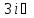
Коммутатор
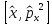 тең:А)
тең:А)
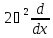 В)
2i
В)
2i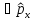
Коммутатор
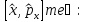
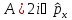
Коммутатор
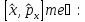 А)
А)
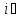
Коммутатор
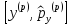 импульс арқылы өрнектелуі:А)
импульс арқылы өрнектелуі:А)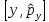
Коммутатор
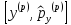 импульс арқылы өрнектелуіА
импульс арқылы өрнектелуіА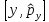 :
А)
:
А)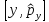 В)
В)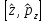
Коммутатор
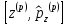 импульс
арқылы өрнектелуі
:А)
импульс
арқылы өрнектелуі
:А)
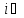 В)
В)
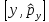 С)
С)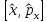
Коммутатор
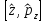 тең:
А)
тең:
А)
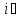 В)
В)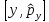
Коммутатор
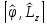 импульс
арқылы өрнектелуі:А)
импульс
арқылы өрнектелуі:А)
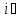
Коммутатор
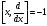 .
Коммутаторлар:А)
.
Коммутаторлар:А)
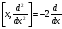 В)
В)
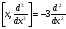 С)
С)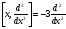
Координата
және
импульс
операторлары
импульсті
өрнектелуде:
А)
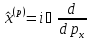 В)
В)
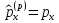
Координата
операторы үшін
кванттық
механикада
дисперсия
 :
а)
:
а)
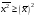 б)
б)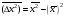 с)
с)
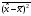
Координата
операторы үшін
кванттық
механикада
дисперсия
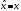 :а)
:а)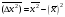 б)
б)
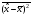
Координата
операторын
импульс
арқылы өрнектеу
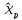 :А)
:А)
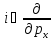
Координаталық
өрнектелуде гармоникалық осциллятор
үшін Шредингер
теңдеуінің шешімі мынадай болады,
мұнда
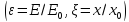 :
А)
:
А)
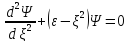
Кордината
операторының коммутаторы
және
бұрыштық моменттің операторы үшін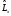 :А)
:А)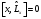 В)
В)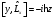 ,
С)
,
С)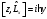
Кордината
операторының коммутаторы және бұрыштық
моменттің операторының компоненті үшін
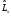 :А)
:А)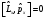 В)
В)
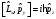 ,
,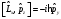
Қандай
да бір А фермиондар жүйесі үшін толқындық
функция құрастыратын болсақ, онда
антисимметрия процедурасы жасалады
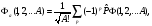 мұнда
мұнда
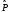 – бөлшектерді ауыстыру операторы,
– бөлшектерді ауыстыру операторы,
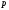 – бұл ауыстыру процесіндегі амалдар
саны. Егер жүйеде үш бөлшек болса, анда
3! Ауыстыру операциясы болады, олар
берілген
– бұл ауыстыру процесіндегі амалдар
саны. Егер жүйеде үш бөлшек болса, анда
3! Ауыстыру операциясы болады, олар
берілген
 функцияға қолданылады, яғни:А)
функцияға қолданылады, яғни:А)
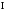 –бірлік оператор, жұптылық
–бірлік оператор, жұптылық
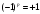 , В)
, В)
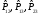 – үш транспозиция, жұптылық
– үш транспозиция, жұптылық
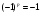 С)
С)
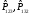 – екі циклді ауыстыру, жұптылық
– екі циклді ауыстыру, жұптылық
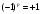
Мезосутегінің
Бордың орбитасы (mπ=273mе,
Бордың сутегінің атомының радиясы
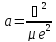 ):
~
):
~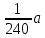
Меншікті
функциялар
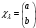 және оператордың меншікті мәндері
және оператордың меншікті мәндері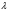 спин операторы болса
спин операторы болса
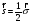 олар мына теңдеуден шығады
олар мына теңдеуден шығады
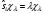 ,
мұнда
,
мұнда
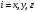 .
Спинорлардың нормировка жасау шарты
.
Спинорлардың нормировка жасау шарты
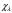 :
А)
:
А)
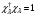 В)
В)
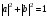
Меншікті
функциялар
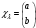 және оператордың меншікті мәндері
және оператордың меншікті мәндері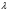 спин операторы болса
спин операторы болса
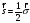 олар мына теңдеуден шығады
олар мына теңдеуден шығады
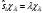 ,
мұнда
,
мұнда
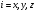 .
Операторлардың меншікті функциялары
мен меншікті мәндерін тап.
А)
.
Операторлардың меншікті функциялары
мен меншікті мәндерін тап.
А)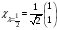 ,
В)
,
В)
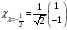 ,
С)
,
С)
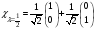
Меншікті
функциялар
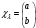 және оператордың меншікті мәндері
және оператордың меншікті мәндері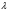 спин операторы болса
спин операторы болса
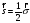 олар мына теңдеуден шығады
олар мына теңдеуден шығады
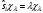 ,
мұнда
,
мұнда
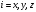 .
Операторлардың меншікті функциялары
мен меншікті мәндерін тап. А)
.
Операторлардың меншікті функциялары
мен меншікті мәндерін тап. А)
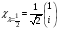 ,
В)
,
В)
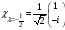
Меншікті
функциялар
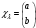 және оператордың меншікті мәндері
және оператордың меншікті мәндері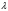 спин операторы болса
спин операторы болса
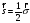 олар мына теңдеуден шығады
олар мына теңдеуден шығады
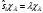 ,
мұнда
,
мұнда
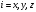 .
Операторлардың меншікті функциялары
мен меншікті мәндерін тап. А)
.
Операторлардың меншікті функциялары
мен меншікті мәндерін тап. А)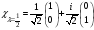 ,
В)
,
В)
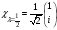 ,
С)
,
С)
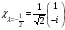
Меншікті
функциялар
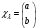 және
оператордың меншікті мәндері
және
оператордың меншікті мәндері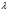 спин
операторы
болса
спин
операторы
болса
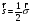 олар мына теңдеуден шығады
олар мына теңдеуден шығады
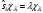 ,
мұнда
,
мұнда
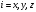 .
Операторлардың
меншікті функциялары мен меншікті
мәндерін тап.
А)
.
Операторлардың
меншікті функциялары мен меншікті
мәндерін тап.
А)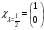 ,
В)
,
В)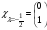
Металдардан электрондардың суық эмиссиясы былай түсіндіріледі: А)Туннель эфектісі мен
Микрожүйелер
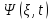 – толқындық функциямен сипатталады
деген ұғым нені білдіреді:
А) постулат
– толқындық функциямен сипатталады
деген ұғым нені білдіреді:
А) постулат
моменттердің
векторлы
қосылу ережелері
(үшбұрыш
ережесі)
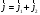 :
А)
:
А)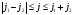 В)
В)
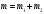 С)
С)
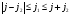 и
и
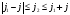
Мына
шарт орындалғанда оператор
түйіндес
болады:
А) транспонирленген
оператор өзінің
түйіндесімен сәйкес болады В)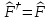 С)
С)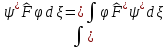
Мына
шарт орындалғанда оператор
Эрмитті
болады:
А)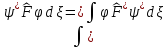 В)
В)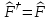
Мына
шартты түсіндір
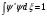 :
А) дискретті спектрлердің толқындық
функциясының нормальдеу шарты ,В)
Заттардың сақталу шарты С) Энергияның
сақталу заңы мен түсіндіріледі
:
А) дискретті спектрлердің толқындық
функциясының нормальдеу шарты ,В)
Заттардың сақталу шарты С) Энергияның
сақталу заңы мен түсіндіріледі
Мына
шартты түсіндір
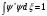 :А)
дискретті спектрлердің толқындық
функциясының нормальдеу шарты , В)
Заттардың сақталу шарты
:А)
дискретті спектрлердің толқындық
функциясының нормальдеу шарты , В)
Заттардың сақталу шарты
Нүктелік
зарядталған бөлшектер үшін кулон
потенциалы
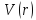 :
А)
:
А)
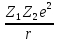
Оператодың
комутаторы
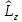
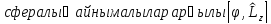 тең:
А)
тең:
А)
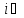
Операторды
квадраттау
нәтижесі:А)
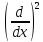 =
=
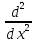 , В)
, В)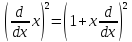 ,
С)
,
С)
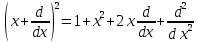
Операторды
кванттау
шарттары
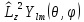 :
А)
:
А)
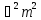
Оператордың
 ,
меншікті
мәнін тап, егер менш.функ.
,
меншікті
мәнін тап, егер менш.функ.
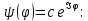 болса:
А)
болса:
А)
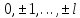
Оператордың
меншікті
функциясын
тап
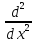 :
А)
:
А)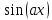
Оператордың
орташа мәні квантты механикада өлшенетін
шама. Математикалық анықтама бер:А)
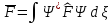
Оператордың
орташа мәні квантты механикада өлшенетін
шама–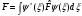 .Базисті
функциямен өрнектегенде, мысалы
.Базисті
функциямен өрнектегенде, мысалы
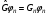 ,өрнек
матрицалық элементтердің комбинациясымен
сипатталады
,өрнек
матрицалық элементтердің комбинациясымен
сипатталады
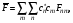 мұнда:
А)
мұнда:
А)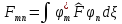 В)
В)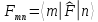
Оператордың
Эквивалентті
жазылуы
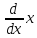 мынадай:А)
мынадай:А)

Операторлар
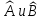 – өз
ара
коммутация
жасамайды және
эрмитті
болады.
Олардың
келесі
комбинациялары
Эрмитті болады:А)
– өз
ара
коммутация
жасамайды және
эрмитті
болады.
Олардың
келесі
комбинациялары
Эрмитті болады:А)
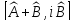 В)
В)
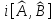 С)
С)
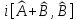
Операторлар
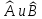 – өз
ара
коммутация
жасамайды және
эрмитті
болады.
Олардың
келесі
комбинациялары
Эрмитті болады:
А)
– өз
ара
коммутация
жасамайды және
эрмитті
болады.
Олардың
келесі
комбинациялары
Эрмитті болады:
А)
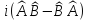 ,
В)
,
В)
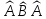 ,
С)
,
С)
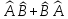
Операторлар
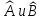 – өз
ара
коммутация
жасамайды және
эрмитті
болады.
Сонда
С операторы Эрмитті болады:
А)
– өз
ара
коммутация
жасамайды және
эрмитті
болады.
Сонда
С операторы Эрмитті болады:
А)
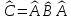
Операторлар
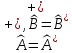 .
Оператор
.
Оператор
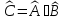 оның
қасиеттері:
А)
оның
қасиеттері:
А)
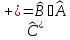
Операторлық
теңдікпен берілген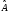 операторының қасиеттері:А)
операторының қасиеттері:А)
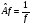 – сызықты
емес В)
– сызықты
емес В)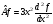 – сызықты,
С)
– сызықты,
С) 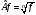 – сызықты
емес
– сызықты
емес
Орбитальдық
бұрыштық моменттің операторлары
өз ара
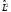 и
и
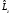 коммутация
жасайды,
олардың
меншікті
функциялар
жүйесі ортақ болады және
квантталады
былайша:
коммутация
жасайды,
олардың
меншікті
функциялар
жүйесі ортақ болады және
квантталады
былайша:
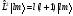 и
и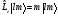 (бұл
(бұл
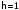 бірлігінде).
Кванттық
сандар
бірлігінде).
Кванттық
сандар
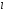 және
және
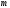 мынадай
мәндер қабылдайды:
А)
мынадай
мәндер қабылдайды:
А)
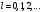 – бүтін
В)
– бүтін
В)
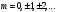 – бүтін,
барлығы
– бүтін,
барлығы
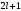 мән
қабылдайды С)
мән
қабылдайды С)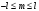 ,
бірлік
шама арқылы
,
бірлік
шама арқылы
Орбитальдық
бұрыштық моменттің операторлары
өз ара
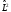 и
и
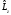 коммутация
жасайды,
олардың
меншікті
функциялар
жүйесі ортақ болады және
квантталады
былайша:
коммутация
жасайды,
олардың
меншікті
функциялар
жүйесі ортақ болады және
квантталады
былайша:
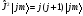 и
и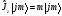 .
Кванттық
сандар
.
Кванттық
сандар
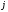 және
және
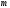 мынадай
мәндер қабылдайды: А)
мынадай
мәндер қабылдайды: А) – бүтін
және жартылай бүтін В)
– бүтін
және жартылай бүтін В)
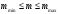 ,
,
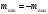 С)
С)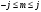 ,
бірлік
шама арқылы
,
бірлік
шама арқылы
Ортақ
меншікті функциялары жоқ операторларды
көрсет:А)
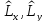 Ауыстырушы
коэффициент
Ауыстырушы
коэффициент
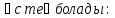 В) 197.33
МэВ фм
В) 197.33
МэВ фм
Орталық
симетриялық потенциалдар да энергетикалық
спектрлердің тозғындалу реті :А)
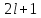 магниттік
кванттық сан m бойынша
магниттік
кванттық сан m бойынша
Орталық
симметриялы өрісте
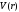 сақталады,яғни қозғалыс интегралы
болатын келесі физикалық шамалар :а)
операторлар
сақталады,яғни қозғалыс интегралы
болатын келесі физикалық шамалар :а)
операторлар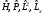 немесе
немесе
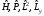 ,
немесе
,
немесе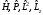 б) жұптылық
б) жұптылық
Орталық-симметриялы
өрістегі әсерлесудің потенциалын
көрсет:а)
Орталық-симметриялы
потенциал өрісі үшін Шредингер теңдеуінің
қасиеттерін көрсет:
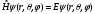 :
А) дискретті шешімдердің спектрі
тозғындалған болады. В) функция
:
А) дискретті шешімдердің спектрі
тозғындалған болады. В) функция
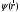 мына операторлар үшін де меншікті болуы
керек
мына операторлар үшін де меншікті болуы
керек
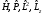 .
С) Бұрыштық тәуелділік
.
С) Бұрыштық тәуелділік
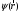 белгілі және ол мына операторлар арқылы
анықталады
белгілі және ол мына операторлар арқылы
анықталады
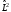 және
және
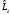 –
–
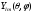
Орталық-симметриялы
потенциал өрісі үшін Шредингер теңдеуінің
шешімдерін көрсет:
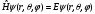 :
А)функция
:
А)функция
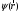 мына операторлар үшін де меншікті болуы
керек
мына операторлар үшін де меншікті болуы
керек
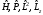 В) Бұрыштық тәуелділік
В) Бұрыштық тәуелділік
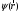 белгілі және ол мына операторлар арқылы
анықталады
белгілі және ол мына операторлар арқылы
анықталады
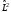 және
және
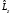 –
–
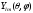
Орын
ауыстыру
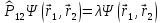 операторының меншікті мәнін
операторының меншікті мәнін
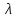 тап . А)
тап . А)
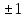
Өлшенетін
шама
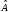 анықталған болатын шарттар:
А)
анықталған болатын шарттар:
А)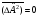 ,
В)
,
В)
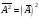 ,
С)
,
С)
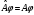
Паули
матрицаларының
көбейтіндісі:
А)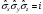 т.б.
цикл
бойынша, В)
т.б.
цикл
бойынша, В)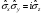 ,
,
 ,
,
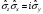 ,
С)
,
С)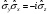 ,
,
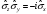 ,
,
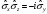
Паули
матрицаларының
көбейтіндісі:
А)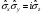 ,
,
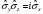 ,
,
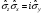 ,
В)
,
В)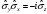 ,
,
 ,
,
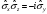
Паули
матрицасының коммутациалық
қасиеттері:
А
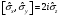 В)
В)
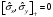
Паули
матрицасының қасиеттері: А)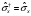 ,
,
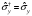 ,
,
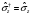 – эрмитті, В)
– эрмитті, В)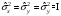 ,
мұнда I – бірлік матрица, С)
,
мұнда I – бірлік матрица, С)
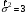
Планетар жүйелердің есептерін шығаруға Шредингера теңдеуін қолдануға мүмкіндік бар ма: а) Мүмкін емес
Потенциалды
өрісте
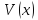 бөлшек үшін туынды
бөлшек үшін туынды
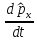 мынадай
болады:а)
мынадай
болады:а)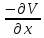
Проекция
операторлары
синглетті
S
= 0 және
триплетті
S
= 1 күйлердегі:
А)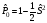 В)
В)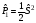 С)
С)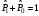
Проекция
операторлары
синглетті
S
= 0 және
триплетті
S
= 1 күйлердегі:
А)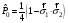 В)
В)
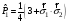 С)
С)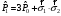
Проекцияның
операторы
үшін
S
= 0 және
S
= 1:
А)
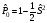 В)
В)
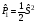
Проекцияның
операторы
синглетті
және
триплетті
күйлер үшін
– S
= 0 және
S
= 1:
А)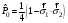 ,
В)
,
В)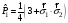
Ритцтың
тікелей вариациялық
әдісінде бірінші қоздырылған күйдегі
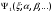 «сынаушы
функцияларға»
қойылатын талаптар:
А)
«сынаушы
функцияларға»
қойылатын талаптар:
А)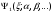 бір
түйіні болуы керек. В) міндетті шарт
бір
түйіні болуы керек. В) міндетті шарт
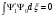 ,
мұнда
,
мұнда
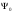 – негізгі күйдегі функция, С)
– негізгі күйдегі функция, С)
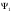 функциясының жұптылығы негізгі күйдегі
функциясының жұптылығы негізгі күйдегі
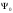 функциясының жұптылығына қарама-қарсы
болуы керек
функциясының жұптылығына қарама-қарсы
болуы керек
Ритцтың
тікелей вариациялық әдісінде негізгі
күйдегі
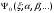 «сынаушы функцияларға» қойылатын
талаптар:
А) Біртекті, үздіксіз, шектелген , В)
Потенциальды шұңқырдың ішінде функция
нольге айналмау керек, С) Функцияның
жұптылығы гамильтонианның
«сынаушы функцияларға» қойылатын
талаптар:
А) Біртекті, үздіксіз, шектелген , В)
Потенциальды шұңқырдың ішінде функция
нольге айналмау керек, С) Функцияның
жұптылығы гамильтонианның
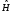 жұптылығымен
анықталады
жұптылығымен
анықталады
Стационар
күйлердің
ерекшеліктері мынада: А)Уақыттан
тәуелділік Е энергия арқылы мына
теңдеуден анықталады
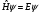 , В) Ықтималдылық тығыздығы уақытқа
тәуелсіз болады , С) Толқындық функциялар
уақыттан тікелей тәуелді болады
, В) Ықтималдылық тығыздығы уақытқа
тәуелсіз болады , С) Толқындық функциялар
уақыттан тікелей тәуелді болады
Стационар
есептерде толқ.функ. уақытқа тәуелділігі
мынадай болады
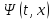 :
: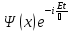
Стационар жүйелерде уақытқа тәуелді болатындар: а) Еркін бөлшектің толқындық функциясы б) дискретті қоздырылмаған спектр үшін толқындық функциялар
Стационар жүйелерде уақытқа тәуелді болатындар: а)Еркін бөлшектің толқындық функциясы б) дискретті қоздырылмаған спектр үшін толқындық функциялар с) дискретті қоздырылған спектр үшін толқындық функциялар
Стационар жүйелерде уақытқа тәуелді болмайтындар: а)гамильтон операторының орташа мәні б) Ықтималдылық тығыздығы
Стационар жүйелерде уақытқа тәуелді болмайтындар:а) гамильтон операторының, импульс моментінің, жұптылықтың операторларының меншікті мәндері б) гамильтон операторының орташа мәні с) Ықтималдылық тығыздығы
Стационар
өрісте
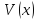 бөлшек
үшін мына қатынас орындалады:а)
бөлшек
үшін мына қатынас орындалады:а)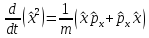
Стационар
теорияда Шредингер теңдеуі шығарылады
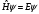 ,
мұнда:
,
мұнда:
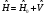 ,
,
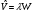 – қоздыру,
– қоздыру,
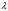 – аз параметр;
– аз параметр;
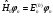 – қоздырылмаған гамильтониан үшін дәл
шешімдер. Бірінші ретті түзету толқындық
функцияға мынадай болады
– қоздырылмаған гамильтониан үшін дәл
шешімдер. Бірінші ретті түзету толқындық
функцияға мынадай болады
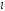 :а)
:а)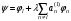 б)
б)
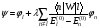 с)
с)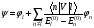
Стационар
теорияда Шредингер теңдеуі шығарылады
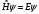 ,
мұнда:
,
мұнда:
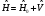 ,
,
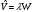 – қоздыру,
– қоздыру,
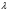 – аз параметр;
– аз параметр;
 – қоздырылмаған гамильтониан үшін дәл
шешімдер. Бірінші ретті түзету энергияға
мынадай болады
– қоздырылмаған гамильтониан үшін дәл
шешімдер. Бірінші ретті түзету энергияға
мынадай болады
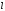 :а)
:а)
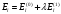 б)
б)
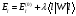
Стационар
теорияда Шредингер теңдеуі шығарылады
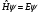 ,
мұнда:
,
мұнда:
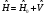 ,
,
 – қоздыру,
– қоздыру,
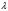 – аз параметр;
– аз параметр;
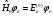 – қоздырылмаған гамильтониан үшін дәл
шешімдер. Бірінші ретті түзету энергияға
мынадай болады
– қоздырылмаған гамильтониан үшін дәл
шешімдер. Бірінші ретті түзету энергияға
мынадай болады
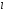 :а)
:а)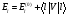 б)
б)
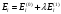 с)
с)
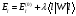
Стационарлық күйлерде: а)Ықтималдылық тығыздығы уақытқа тәуелді емес б) Толқындық функция уақытқа тікелей тәуелді
Суперпозиция
принципі бойынша:
А) Егер жүйе қандай да
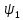 и
и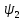 ,
күйлерде орналасатын болса, онда жүйе
келесі
,
күйлерде орналасатын болса, онда жүйе
келесі
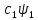 +
+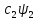 күйінде де орналаса алады.
күйінде де орналаса алады.
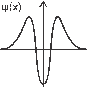
Суретте
бір өлшемді гармоникалық осцилятордың
толқындық функциясы көрсетілген.Функцияның
екі түйіні бар. Бұл күйде: А)
Орташа кинетикалық
энергия
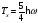 ,
В)Орташа
потенциалдық
энергия
,
В)Орташа
потенциалдық
энергия
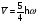 С)
Анықталмағандық қатынастар
С)
Анықталмағандық қатынастар
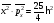
Суреттегі
I
облыс үшін Шредингер теңдеуі былай
жазылады:А)
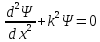
Суреттегі
толқындық функция шексіз қабырғалы
потенциальды шұңқырда микробөлшек
үшін қандай күйді сипаттайды:
1-ші қоздырылған күй![]()
Сутегі атомы деңгейінің тозғындалуы n=6: А)36
Сфералық
симметриялы потенциал үшін шешімдер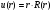 Шредингер теңдеуінің радиал шешімдері
болады:
А)
Шредингер теңдеуінің радиал шешімдері
болады:
А) ,
где
,
где
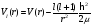 ,
,
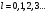 ,В)
,В)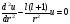 ,
,
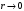 жағдайда
С)
жағдайда
С)
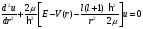
Сызықты
берілген оператор
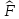 үшін
мына оператор
эрмитті:
а)
үшін
мына оператор
эрмитті:
а)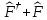 б)
б)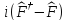
Сызықты
берілген оператор
 үшін
мына оператор
эрмитті:а)
үшін
мына оператор
эрмитті:а)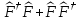 б)
б)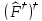
Сызықты
берілген оператор үшін
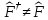 мына
операторлар
эрмитті:
а)
мына
операторлар
эрмитті:
а)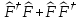 б)
б)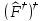 с)
с)