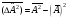- •V(X) потенциалдық өрісте қозғалатын бөлшектің іргелі операторларының уақыт бойынша толық туындысы:е)
- •Орталық симметриялы өрісте r(r) радиалды функция үшін Шредингердіңрадиалды теңдеуі:
- •Сызықтық гармоникалық оператордың импульстік көріністегі толқындық функциясы: ,
- •Сызықтық гармоникалықоператордың импульстік көріністегі толқындық функциясы:
- •Гейзенбергтің анықталмағандық принципі тек қана мына щамалармен сипатталады:а)
- •Кванттық механикадағы коммутатор:а)
- •Сызықты гармоникалық осцилляторды кванттау шарттары: а)
- •Сызықты гармоникалық осцилятордың уақытқа тәуелділігі .:а)
- •Сызықтық гармоникалық осциллятордың толқындық функциясының асимптотикасы былай жазылады:
- •Тік бұрышты бір өлшемді шұңқырда Электрон негізгі күйде орналасқан . Бұл күйдегі импульстің орташа мәні : а)
Гейзенбергтің анықталмағандық принципі тек қана мына щамалармен сипатталады:а)
Дискретті
азғындалған
спектрдің
функциясының ортонормировка
жасау шарты:
А)
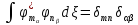
Дискретті
азғындалмаған
спектрдің
меншікті функциясының толық болу шарты:
А)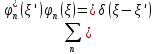
Егер
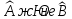 –
коммутация
жасаса,
онда
келесі операторларды мына түрде жазуға
болады: а)
–
коммутация
жасаса,
онда
келесі операторларды мына түрде жазуға
болады: а)
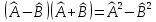 б)
б)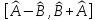 =0
с)
=0
с)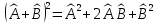
Егер
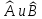 – коммутация
жасамаса
и эрмитті
болса,
онда
келесі операторларда эрмитті болады:
а)
– коммутация
жасамаса
и эрмитті
болса,
онда
келесі операторларда эрмитті болады:
а)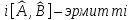 б)
б)
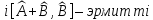 С)
С)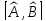 –эрмитті емес
–эрмитті емес
Егер
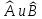 – коммутация
жасамаса,
онда
төмендегідей қатынас жазуға болады
А):
– коммутация
жасамаса,
онда
төмендегідей қатынас жазуға болады
А):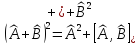 В)
В)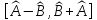 =2
=2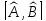 С)
С)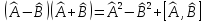
Егер бөлшектердің де Бройль толқын ұзындығы бірдей болса,онда көбірек жылдамдыққа ие болатын бөлшек: А) электрон В) позитрон
Егер екі кванттық –механикалық шамалар комутация жасаса,онда: а) Олардың меншікті функциялар жүйесі ортақ болады және олардың шамаларын бір тәжірибеде есептеуге болады
Егер екі оператор коммутация жасаса , онда: а) Олардың меншікті функциялар жүйесі ортақ болады.б) Олардың орташа мәнін бір тәжірибеде есептеуге болады с) анықталмағандық қатынасына бағынады
Егер
жүйеде үш бөлшек берілсе, онда 3! ауысу
операциясы болды, бұл операция мына
функцияға
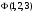 қолданылады.
Антисимметриялы операторды
қолданылады.
Антисимметриялы операторды
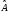 және симметриялы операторды
және симметриялы операторды
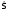 қолдансақ,
онда симметриялы
функцияны
қолдансақ,
онда симметриялы
функцияны
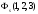 ,
және антисимметриялы
,
және антисимметриялы
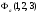 функцияны
құрастыруға болады:а)
функцияны
құрастыруға болады:а)
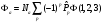 и
и
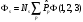 б)
б)
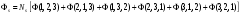 с)
с)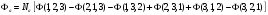
Егер
меншікті функция
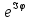 :болса,
онда оператордың
:болса,
онда оператордың
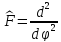 меншікті
мәнін тап: А)
меншікті
мәнін тап: А)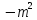
Екі оператор коммутация жасайды.бұл жағдайда: а)Олардың жалпы меншікті функциялар жүйесі болады б)ортақ болады с) олардың орта шамасын бір тәжірибеде өлшеуге болады
Екі
бөлшектің моменттері мынандай
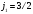 және
және
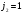 олар өзара жүйе құрайды,толық моменті
олар өзара жүйе құрайды,толық моменті
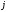 және
проекциясы
және
проекциясы
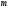 :а)
:а)
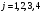 б
б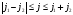 б)
б)
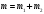 ,
,
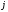 берілген
жағдайда
берілген
жағдайда
Екі
оператор
коммутация
жасайды,яғни:
а)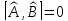 б)
б)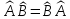
Екі
өлшемді гармоникалық осциллятордың
нольдік энергиясы мынадай болады:А)
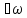
Екі
тепе-тең бөлшек үшін белгілі симметриясы
бар толқындық функцияларды құру принципі:
Гамильтонианы белгілі Шредингер теңдеуі
үшін
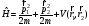 мынадай шешім бар
мынадай шешім бар
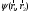 .
Функция
.
Функция
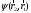 берілген
мына функциядан
берілген
мына функциядан
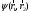 шығады, мұнда
шығады, мұнда
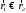 айнымалыларын ауыстырамыз, содан
симметриясы белгілі функция құрастырылады:А)
айнымалыларын ауыстырамыз, содан
симметриясы белгілі функция құрастырылады:А)
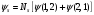 ,
В)
,
В)
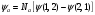
Ені
берілген потенциальды шұңқырдағы
бөлшектің туннельді эффектінің табылу
ықтималдылығы (а – ені,
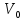 – барьердің биіктігі, m –бөлшектің
массасы,
– барьердің биіктігі, m –бөлшектің
массасы,
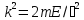 ,
,
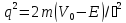 ):
А)
):
А)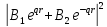
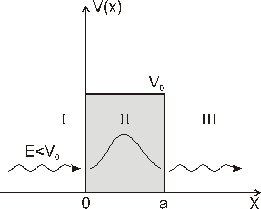
Ені
шектелген потенциалды шұңқыр үшін (а –
ені,
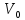 – тосқауыл биіктігі, m – бөлшек массасы
)
бөлшектер
ағыны түседі. Суреттегі II облыс үшін
Шредингер теңдеуі былай жазылады:А)
– тосқауыл биіктігі, m – бөлшек массасы
)
бөлшектер
ағыны түседі. Суреттегі II облыс үшін
Шредингер теңдеуі былай жазылады:А)
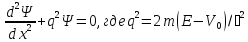 В)
В)
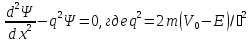
Ені
шектелген потенциальды тосқауылға (а
– ені,
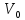 – тосқауыл биіктігі, m – бөлшек массасы,
– тосқауыл биіктігі, m – бөлшек массасы,
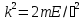 ,
,
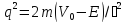 )
бөлшектер ағыны түседі.
)
бөлшектер ағыны түседі. 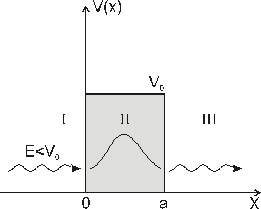
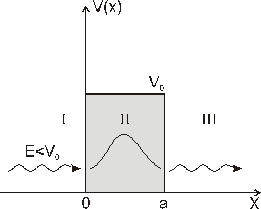
Ені
шектелген потенциальды тосқауылға (а
– ені,
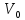 – тосқауыл биіктігі, m – бөлшек массасы,
– тосқауыл биіктігі, m – бөлшек массасы,
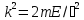 ,
,
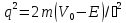 )
бөлшектер ағыны түседі. Суреттегі II
облыс үшін Шредингер теңдеуі былай
жазылады:А)
)
бөлшектер ағыны түседі. Суреттегі II
облыс үшін Шредингер теңдеуі былай
жазылады:А)
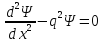 .
.
Еркін
бөлшек берілген yz жазықтығында қозғалады.
Бөлшекті
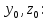 нүктесінде
табу ықтималдылығы, А)
нүктесінде
табу ықтималдылығы, А)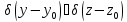
Еркін
бөлшектің
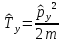 операторының
меншікті мәнін тап
:А)
операторының
меншікті мәнін тап
:А)
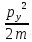
Еркін
бөлшектің
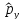 операторының меншікті мәнін тап
:А)
операторының меншікті мәнін тап
:А)
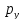
Жартылай
спині бар екі бөлшек берілген
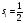 ,
,
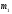 және
және
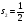 ,
,
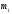 олар жүйе құрайды,қосынды моменті
олар жүйе құрайды,қосынды моменті
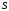 және
оның проекциясы
және
оның проекциясы
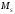 .
Оператор-проекторлар
синглетті және триплетті күйлерде
меншікті функция теңдеуін қанағаттандырады
және меншікті мәндері мынадай–
.
Оператор-проекторлар
синглетті және триплетті күйлерде
меншікті функция теңдеуін қанағаттандырады
және меншікті мәндері мынадай–
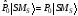 және
және
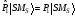 ,
,
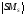 функциясы да бұл операторлар үшін
меншкті болады
функциясы да бұл операторлар үшін
меншкті болады
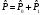 ,
меншікті
мәні
,
меншікті
мәні
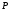 :
а)
:
а)
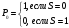 б)
б)
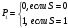 с)
с)
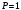 үшін
үшін
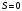 және
және
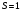
Импульс
моменті проекциясы операторы үшін
кванттық
механикада
дисперсия
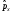 :а)
:а)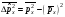 б)
б)
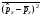
Импульс
операторын
импульс
арқылы өрнектеу
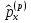 :А)
:А)
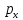
Импульс
проекциясы операторы үшін
кванттық
механикада
дисперсия
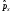 :а)
:а)
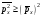 б)
б)
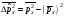 с)
с)
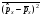
Импульс
проекциясы операторының
коммутаторы және бұрыштық моменттің
операторының компоненті үшін:
А)
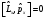 В)
В)
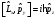 С)
С)
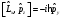
Импульс
проекциясы операторының коммутаторы
және бұрыштық моменттің операторының
компоненті үшін
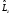 :
А)
:
А)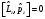 В)
В)
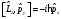 ,
,
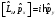
Импульс
проекциясы операторының коммутаторы
және бұрыштық моменттің операторының
компоненті үшін
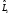 :А)
:А)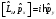 В)
В)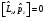 С)
С)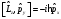
Импульс
проекциясының операторының
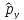 меншікті
функциясы
меншікті
функциясы
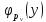 :
А)
:
А)
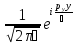
Импульс
сипатталуындағы гармоникалық осциллятордың
энергетикалық спектрінің
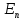 квантталу шарттары
квантталу шарттары
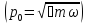 :
А)
:
А)
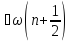
Импульсті
өрнектелудегі сызықтық гармоникалық
осциллятордың Шредингер теңдеуі:А)
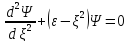
Каноникалық түйіндес шамалар: А)(x ,px), (y, py), (z, pz),В) (E, t)
Кванттық
жүйелердің негізгі күйін вариациялық
әдіспен есептегенде
алдымен аналитикалық
жолмен
қандай да «сынаушы функция»
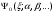 алынады, онда белгісіз параметрлер бар
алынады, онда белгісіз параметрлер бар
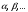 және энергетикалық функционал есептеледі
және энергетикалық функционал есептеледі
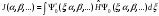 .
Сондағы негізгі күйдегі энергияның
есептелуі: А) Белгісіз
шамалар
.
Сондағы негізгі күйдегі энергияның
есептелуі: А) Белгісіз
шамалар
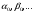 функцияның минимумы бойынша
функцияның минимумы бойынша
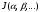 ,
В)
,
В)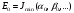 есептеледі, С) Теңдеулер жүйесі есептеледі
есептеледі, С) Теңдеулер жүйесі есептеледі
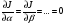
Кванттық механикада вариациялық әдіс рұқсат береді: а) Дискретті деңгейлердің энергетикалық спектрін есептеуге. б) Жүйенің Гамильтонының меншікті функцияларын есептейді
Кванттық
механикада вариациялық әдіс рұқсат
береді:
а) Дискретті деңгейлердің энергетикалық
спектрін есептеуге. б) энергетикалық
спектрлердің есептерінің дәлдігін
бақылайды с) Жүйенің Гамильтонының
меншікті функцияларын есептейді
Кванттық
механикада
дисперсия
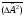 :
а) Оң анықталған болады б)
:
а) Оң анықталған болады б)
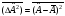 с)
с)
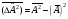
Кванттық
механикада
дисперсия
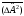 :а)
:а)
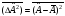 б)
б)