
- •Цель работы
- •Приборы магнитоэлектрической системы
- •Приборы электромагнитной системы
- •Приборы электродинамической и ферродинамической систем
- •Шкала прибора
- •Точность измерительных приборов
- •Сведения о технических данных измерительных приборов
- •Включение приборов для измерения тока, напряжения, мощности
- •Практическая часть
- •Цель работы
- •Приборы и оборудование
- •Программа работы и указания по ее выполнению
- •Теоретическая часть работа и мощность электрического тока.
- •Практическая часть
- •Цель работы
- •Приборы и оборудование
- •Программа работы и указания по ее выполнению
- •Теоретическая часть применение закона ома и законов кирхгофа для расчетов электрических цепей
- •Метод двух узлов
- •Метод контурных токов
- •Практическая часть
- •Цель работы
- •Приборы и оборудование
- •Программа работы и указания к ее выполнению
- •Теоретическая часть
- •Практическая часть
- •Справочный материал по электронике
- •2. Источники вторичного электропитания
- •3. Аналоговая электроника
- •3. Цифровая электроника
- •Триггер
- •4. Цифровые системы
- •Цифро-Аналоговые преобразователи
- •Преобразователи напряжения в код
Практическая часть
|
№ опыта |
I, А |
U, В |
UR, B |
UС, В |
UL, B |
Р, Вт |
f, Гц |
|
1 |
0,525 |
100 |
83 |
48 |
10 |
47 |
50 |
|
2 |
0,55 |
100 |
86,9 |
- |
10,5 |
50,1 |
50 |
|
3 |
0,525 |
100 |
83 |
48 |
- |
43,6 |
50 |

Расчеты
I. Опыт № 1.

Рисунок 1.
Вычисление
 ,
, иR
иR

2) Вычисление
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() и
и![]()


Вычисление
 и
и 
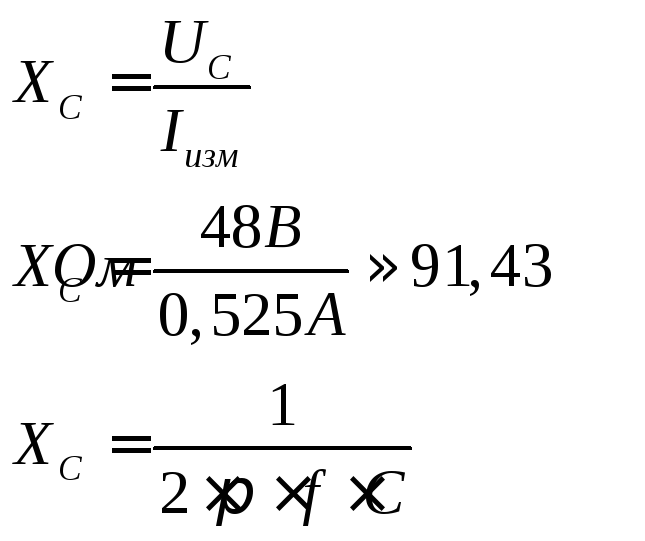


II. Опыт № 2.

Рисунок 2.
Вычисление
 и
и


Вычисление
 ,
, ,
,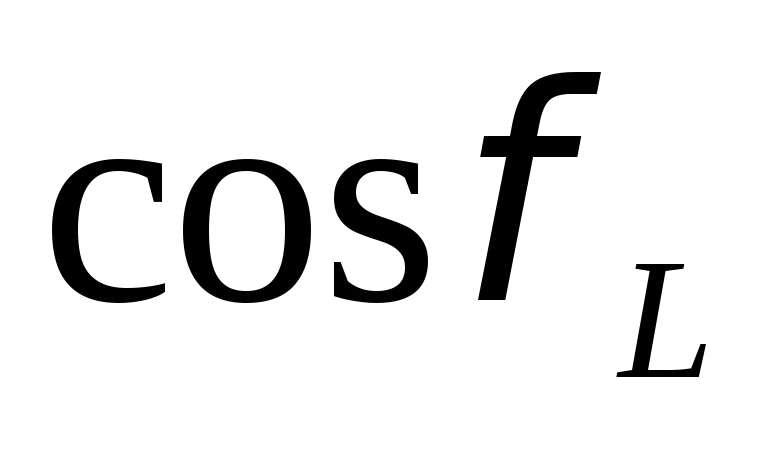 ,
, ,
, и
и




III. Опыт № 3.

Рисунок 2.
Вычисление
 и
и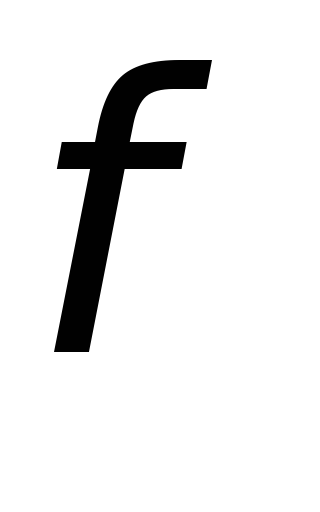

Вычисление
 и
и 


|
№ |
cosφ |
φ,° |
cosφL |
φL,° |
R,Ом |
ХС,Ом |
С,Ф |
ZL,Оm |
RL,Ом |
XL,Oм |
Lк, Гн |
|
1 |
0,895 |
26,52 |
0,648 |
49,61 |
158 |
91,43 |
34,8 |
19,05 |
12,34 |
14,51 |
0,046 |
|
2 |
0,9109 |
20,45 |
0,648 |
49,64 |
158 |
- |
- |
19,05 |
12,34 |
14,51 |
0,046 |
|
3 |
0,83 |
33,85 |
- |
- |
158 |
91,43 |
34,8 |
- |
- |
- |
- |
Вывод:
В ходе данной лабораторной работы …
Магнитные цепи
Магнитные величины
В магнитном поле как особом состоянии среды распределение энергии обусловлено движением электрических зарядов или изменением электрического поля, т. е. электрическим током.
Направление магнитного потока определяют по направлению магнитной стрелки, помещенной в это поле. Магнитное поле представляется в виде направленного магнитного потока Ф, линии которого всегда замкнуты.
В качестве физической величины, характеризующей интенсивность магнитного потока Ф, служитвекор магнитнойиндукции В, направление которого совпадает с направлением магнитного потока. Единицей магнитного потока в системе СИ является вебер (Вб); 1 Вб = 1 В∙с.
За единицу магнитной индукции принимают индукцию, при которой через площадь s в 1 м2, расположенную перпендикулярно направлению магнитного потока, проходит поток в 1 Вб. Магнитную индукцию выражают в теслах (Тл): 1 Тл = 1 Вб/м2= 1 В·с/м2.
Способность источника магнитного поля (электрического тока) создавать магнитный поток характеризуется напряженностью магнитного поля Н, выражаемой в А/м.

Рис.1
В воздухе
направление векторов магнитной индукции
![]() и напряженности
магнитного поля
и напряженности
магнитного поля ![]() совпадают и
связаны соотношениемН = В/μ0,
где μ0=4π∙10-7Гн/м - магнитная
постоянная.
совпадают и
связаны соотношениемН = В/μ0,
где μ0=4π∙10-7Гн/м - магнитная
постоянная.
Количественные соотношения, характеризующие
магнитное поле, основаны на законе
полного тока. Этот закон устанавливает
связь между напряженностью магнитного
поля Нв любой точке замкнутого
контура вокруг проводника с токомI.
Например, напряженность в точкеА
(рис. 1, а) равна![]()
где 2πr - длина контура, охватывающего проводник, r - радиус контура.
Если действует п проводников с токомI, то напряженность в точкеА равна:Н =пI/(2πr). Напряженность поля в центре однослойной катушки (когда l>>r) (рис. 1, б) с числом витков ωравнаH= ωI/l.
Произведение ωI называют магнитодвижущей силой (мдс) и выражают в амперах.
Потокосцепление катушки: ψ=ωФ. В линейной катушке индуктивности потокосцепление пропорционально току.
Коэффициент пропорциональности L=ψ/I называют индуктивностью. Единица индуктивности — генри (Гн). На практике применяют доли; милли- и микрогенри: 1 мГн = 10-3 Гн; 1 мкГн = 10-6 Гн.
Энергия магнитного
поля катушки индуктивности (Дж)
определяется работой, совершаемой
электрическим током в процессе
создания магнитного поля:![]()
Магнитные цепи
Классификация магнитных цепей. Элементы магнитной цепи.
Магнитная система является одним из основных элементов электрических машин и ряда электротехнических устройств.В магнитную систему входят источники магнитного поля (обмотка с током, возбуждающая магнитное поле, постоянный магнит)и система магнитопроводов из ферромагнитного материала, по которым замыкается магнитный поток.
При анализе магнитных цепей магнитную систему электротехнического устройства представляют, как и в электрических цепях, эквивалентной схемой.
Магнитные цепи бывают неразветвленные и разветвленные, однородные и неоднородные, симметричные и несимметричные.
Неразветвленной магнитной цепью называют цепь, через элементы которой замыкается один и тот же магнитный поток.
В разветвленной магнитной цепи содержатся ветви, в каждой из которых замыкаются свои магнитные потоки.
В однородной магнитной цепи, образованной замкнутым магиитопроводом, магнитный поток находится в однородной среде.
Неоднородной называют магнитную цепь, состоящую из участков, имеющих разные сечения, воздушные зазоры, ферромагнитные тела с различными магнитными свойствами.
Из физики известна
способность вещества под воздействием
напряженности
внешнего магнитного поля Н
создавать
собственное поле, называемое
намагниченностью
М, которая
характеризуется магнитной восприимчивостью
χ:![]() .
При этом
магнитная индукция в веществе
.
При этом
магнитная индукция в веществе
![]()
где
![]() .
.![]() - относительная и абсолютная магнитныепроницаемости,
соответственно.
- относительная и абсолютная магнитныепроницаемости,
соответственно.
Вещества, имеющие высокое значение магнитной восприимчивости, называют ферромагнитными, или магнитными.
К ним относятся железо (Fe), кобальт (Со), никель (Ni), редкоземельные элементы: гадолиний (Gd), диспрозий (Dy) и др., а также сплавы на базе этих элементов.
Зависимость магнитной индукции в веществе (материале) от напряженности внешнего магнитного поля В(Н) носит нелинейный характер: по мере увеличенияН индукцияВсначала возрастает резко, а затем, приближаясь к области насыщения, процесс намагничивания материала замедляется и прекращается, когда резервы ферромагнетика оказываются исчерпанными Рис.2.

Рис.2.

Рис.3. а – однородная неразветвлённая; б – неоднородная неразветвлённая; в - неоднородная разветвлённая.
Если элемент магнитной цепи, например цилиндр из ферромагнитного материала, поместить в однородное магнитное поле,он намагнитится. Если после намагничивания до состояния насыщения внешнее поле убрать (уменьшить до нуля), то цилиндрявится источником магнитного поля за счет намагниченности материала — остаточной намагниченности. Чтобы разрушить эту остаточную намагниченность, нужно создать внешнее поле, направленное противоположно полю, создаваемому цилиндром,для преодоления задерживающей, так называемой коэрцитивной силы Нс, которая стремится сохранить созданную микротоками намагниченность.
В зависимости от значения коэрцитивной силы Нс все магнитные материалы принято делить намагнитомягкие и магнитотвердые.
Магнитомягкие материалы имеют малую коэрцитивную силу (крутоподнимающаяся основная кривая намагничивания и относительно малая площадь петли гистерезиса) Рис.6.
Петля циклического перемагничивания. Явление запаздыванияВотН– магнитный гистерезис.

Рис.4. Нс- остаточная намагниченность (значение напряженности для полного размагничивания сердечника) коэрцитивная сила,Вr- остаточная магнитная индукция

Рис.5. АС и АС – предельная петля гистерезиса

Рис.6. Разные материалы с одной скоростью перемагничивания.
1 - магнитножесткие материалы – с большими значениями коэрцитивной силой (Нс – более 40 а/см) и остаточной магнитной индукцией Вr– 1;
2 – магнитномягкие(малая коэрцитивная сила –от единиц до десятков ампер и высокая магнитная проницаемость с малыми потерями на перемагничивание)

Рис.7. Частные циклы перемагничивания. Коэф. возврата В2– В1/ В1 – D
Расчет магнитной цепи
Аналогия между магнитной и электрическойцепями.
Расчет магнитных цепей производится на основе закона полного тока с помощью уравнений магнитного состояния.
Как и в электрических цепях, здесь используют уравнения магнитного состояния:
узловое — алгебраическая
сумма магнитных потоков, сходящихся в
любом узле (поток через замкнутую
поверхность), всегда равна нулю:![]()
контурное — алгебраическая сумма
падений магнитных напряжений в любом
замкнутом контуре магнитной цепи равна
алгебраической сумме магнитодвижущих
сил в контуре:![]()
Падение магнитного напряжения на
заданном участке магнитной
цепи определяют как произведение
напряженности магнитного поля на длину
участка цепи (или магнитного сопротивления
участка на магнитный поток) и выражают
в амперах:![]() ,
,
где![]() - магнитное сопротивление участка. Для
воздушного зазора
- магнитное сопротивление участка. Для
воздушного зазора![]() и
и![]() .
.
Зависимость магнитного потока Ф от
магнитодвижущей силы ωI
и магнитных сопротивленийRμучастков магнитнойцепи
получают из уравнения магнитного
состояния ветви магнитной цепи![]() и записывают в виде формулы:
и записывают в виде формулы:
![]()
Между вебер-амперными характеристиками Ф(I) в магнитных цепях и вольт-ампернымиU(I) в электрических цепях существует полная аналогия. Для магнитной цепи можно изобразить аналогичную режиму нагрузки электрической цепи, схему замещения.

Рис.8.
Например, для
магнитной цепи рис. 3, б
она имеет
вид, представленный на рис. 8, а.
Схема содержит
источник магнитодвижущей силыωI
и два участка с магнитными сопротивлениями
Rμм
и Rμв.
Как и для электрической цепи, можно
записать уравнение магнитного
состояния![]()
где
![]() -
магнитное напряжение научастке
ферромагнетика;
-
магнитное напряжение научастке
ферромагнетика;
![]() - магнитное
напряжение на участке рабочего
воздушного зазора.
- магнитное
напряжение на участке рабочего
воздушного зазора.
Методы расчета магнитной цепи
При расчете магнитной цепи могут быть две задачи: прямая, когда известны геометрические размеры и магнитные свойства материала магнитопровода, а также значение магнитного потока Ф (определяются магнитодвижущая сила и токIв витках обмотки), иобратная, когда задается магнитодвижущая сила, геометрические размеры и материалы магнитопровода (определяется магнитный поток Ф).
Рассмотрим прямую задачу. В неразветвленной и неоднородной магнитной цепи (см. рис. 3,б) известны: значение магнитного потока в воздушном зазоре Ф, геометрические размеры и материал магнитопровода, число витков обмоткиω, а также зависимостьВм(Н) (рис. 8,б).Определить мдсωI.
ПРИМЕР Алгоритм расчета магнитной цепи можно представить в следующем виде:
По заданным геометрическим размерам определяем Sм; Sв; lм и lв.
По заданному магнитному потоку Ф определяем магнитные индукции Вм, Ввна участках магнитной цепи.
Цепь одноконтурная, следовательно, магнитный поток Ф во всех участках цепи будет неизменным. Полагая Sв = Sм получим
![]()
3. По вычисленным Вми кривой намагничиванияВ(Н) для заданного материала магнитопровода находимНм (рис.8,б).
4. Обходя контур в направлении магнитного потока, запишем уравнение магнитного состояния
![]()

здесь
![]() — напряженность магнитного поля в
воздушном зазоре.
— напряженность магнитного поля в
воздушном зазоре.
Таким образом, расчетное уравнение
примет вид![]()
В обратной задаче расчета магнитной цепи задается мдсωIи требуется определить магнитный поток Ф на участке цепи (или в воздушном зазоре).
Из-за нелинейности зависимость Ф (ωI) необходимо предварительно рассчитать и построить, а затем для заданного значенияωIопределить Фв. Для построения зависимости Ф(ωI) задают 5—7 значений магнитного потока, по алгоритму «прямой задачи» рассчитывают соответствующие значения мдс и строят зависимости Ф(ωI).
Во многих электротехнических устройствах (электрических машинах, трансформаторах и др.) используют симметричные магнитные системы (см. рис. 3,в).В цепи такой системы магнитный потокФ1равен потоку Ф2. В среднем сердечнике магнитопровода оба потока Ф1 и Ф2 складываются, но и сечение сердечника вдвое больше сечения крайних сердечников. При расчете такую цепь можно представить как две самостоятельные, еслимысленно разделить магнитопровод по вертикальной оси ab. Магнитные потоки Ф1и Ф2при таком делении останутся неизменными по направлению. Иными словами, схему замещения магнитной цепи такой магнитной системы можно представитьдвумя независимыми неразветвленными магнитными цепями, в которых действуют одинаковые мдс, и рассчитывать одну из двух составляющих. При решении прямой задачи, когда задан магнитный поток Ф в любом стержне, полученное значение мдсравно значению полной мдс. При решении обратной задачи значение магнитного потока в среднем стержне Ф1 определяют на основании уравнения состояния узла.
Магнитная цепь с постоянными магнитами
В магнитных системах с постоянными магнитами поле в воздушном зазоре создается под воздействием энергии постоянного магнита. В качестве примера на рис. 9,а представлена магнитная цепь магнитоэлектрического прибора, состоящая из постоянного магнита, элементов из магнитомягкого материала и двух воздушных зазоров. Схема замещения этой цепи показана на рис. 8.

Рис.9.
Учитывая, что магнитное сопротивление
ферромагнитных элементов мало по
сравнению с сопротивлением воздушных
зазоров, схема замещения упрощается и
уравнение по закону полного тока имеет
вид
![]()
Зная характеристику магнитотвердого
материала В(Н) и полагая, что![]() и
и![]() получим
получим![]()
Это уравнение показывает, что зависимость
Вв(H)— прямая во втором квадранте (рис. 9,б).ОпределяемВв графическим
методом. Для этого во втором квадранте
строится кривая размагничивания
материалаВ(Н) и из начала осей
координат проводится прямая под углом![]() .
ТочкаК пересечения кривойВм(Н)
и прямой
.
ТочкаК пересечения кривойВм(Н)
и прямой![]() (рис. 9, б) соответствует значению индукции
в зазорахВв и магнитного
потока Фв=BвS.
(рис. 9, б) соответствует значению индукции
в зазорахВв и магнитного
потока Фв=BвS.
ВАЖНОЕ
Ферромагнитные материалы в магнитопроводах электромагнитных устройств усиливают магнитное поле, создаваемое током намагничивающей катушки.
Изменение воздушного зазора в магнитопроводе цепи постоянного тока приводит к изменению магнитного потока в рабочем зазоре: с увеличением воздушного зазора магнитный поток уменьшается.
Ферромагнитные материалы бывают магнитомягкие с малой коэрцитивной силой (единицы А/см) и магнитотвердые с большой коэрцитивной силой (десятки и сотни А/см). Магнитомягкие материалы используют в магнитопроводах различных электромагнитных устройств; магнитотвердые материалы — для изготовления постоянных магнитов и магнитных систем.
4. Расчет магнитных цепей с ферромагнитными элементами аналогичен расчету электрических цепей постоянного тока с нелинейным элементами.
5. При расчете магнитных цепей, как и электрических, используют узловые и контурные уравнения.
Справочный материал по электрическим машинами трансформаторам
Машины постоянного тока
Так, из закона электромагнитной индукции следует, что если проводник перемешать перпендикулярно линиям магнитного поля, то в нем будет наводиться эдс, а ее значение определится формулойе = Blυ,
где В — магнитная индукция, В∙с/м2;l,υ — длина, м, и скорость, м/с, перемещения проводника.
Под действием эдс в проводнике, замкнутом на резистор, возникает ток в направлении, совпадающем с направлением эдс. В результате взаимодействия проводника с током и магнитного поля возникнет электромагнитная сила, которая определяется по формуле Fэм=ВIl, а ее направление — поправилу «левой руки».
Уравнение электрического состояния генератора,Е = U + Rя I или U = Е - Rя I
Уравнение электрического состояния двигателя, Е = U - Rя I или U = Е + Rя I
Действующее значение эдс в витке
![]()
Среднее значение эдс в витке в
предположении, чтоФ=Всрlτ
равно
![]()
Если общее число витков, соединенных
последовательно, одной параллельной
ветви равно N/(2а), то эдс на щетках
![]() ,
,
где сЕ=pN/(60a) — конструктивная постоянная обмотки;N — число проводников;а — число параллельных ветвей.
Электродвижущая сила одной фазы якорной
обмотки
![]()
где Eв — эдс витка;kоб — обмоточный коэффициент, учитывающий тип обмотки и отличие геометрической суммы эдс витков от арифметической;w — число витков фазы.
Внешнии характеристики при различных способах возбуждения генератора Рис.1.
 Рис.1.
Рис.1.
1 Характеристика холостого хода генератора ПТ с независимым возбуждением
2 Внешняя характеристика генератора ПТсо смешанным возбуждением
3 Внешняя характеристика генератора ПТс независимым возбуждением
4 Внешняя характеристика генератора ПТс последовательным возбуждением
5 Внешняя характеристика генератора ПТс параллельным возбуждением
Универсальная характеристика машины параллельного возбуждения Рис.2.
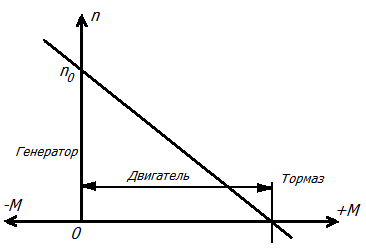
Рис.2
1 - Режим генератора, 2 - Режим двигателя, 3 - Режим электромагнитного тормаза

Рис.3. Независимое возбуждение – а;параллельное возбуждение –б; последовательное возбуждение –в; смешанное –г.
Двигатель Постоянного Тока

Рис.4. а -универсальная характеристика машины параллельного возбуждения;
б - механическая характеристика двигателя последовательного возбуждения;
в - механическая характеристика двигателя смешанного возбуждения;
г - механическая характеристика двигателя параллельного возбуждения.
Самовозбуждение генератора происходит при наличи трёх условий
Остаточного магнитного потока, создающего Еост
Совпадающего направления поля обмотки возбуждения с направлением остаточного магнитного потока
Сопротивления обмотки возбуждения (при параллельном возбуждении) меньше критического, т.е. когда ток возбуждения способен достигать значения, обеспечивающего на характеристике холостого хода заданное значение ЕА . (RB >RKP)

Рис.5 Графическое определение режима генератора при самовозбуждении.
Синхронный генератор
Синхронной называется электрическая машина, частота вращение которой связана постоянным отношением с частотой сети переменного тока, в которую машина включена.

Рис.6. Характеристика холостого хода синхронного генератора или магнитная характеристика (влияние тока возбуждения на ЭДС)
Рис.7. Зависимости кпд синхронного генератора от нагрузки при различных коэффициентах мощности
Энергетические потери и диаграммы
Энергетические потери синхронного генератора делятся на постоянные – механические, возбуждения и в стали, а переменные потери – меди и добавочные
КПД синхронного генератора описываются формулой
η= 3UIcosφ/(3UIcosφ +Pпост + Pперем)
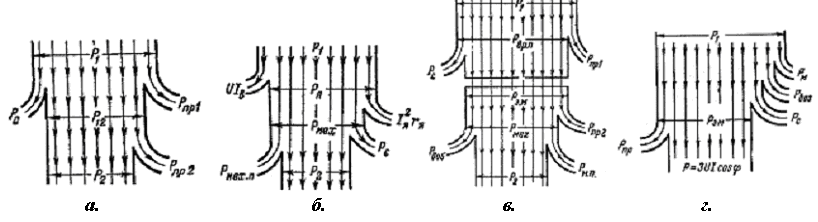
Рис.8 а - энергетическая диаграмма трансформатора;б - энергетическая диаграмма двигателя постоянного тока;в - энергетическая диаграмма асинхронного двигателя;г - энергетическая диаграмма синхронного генератора.
Максимальная частота вращения синхронной машины в сети переменного тока с частотой 50 Гц - 2πf(3000)
Если количество пар полюсов р1>р2, то частота вращения ротора -n1<n2
синхронной машины уменьшится. (n=2πf/p)
У гидрогенераторов первичным двигателем является гидротурбина, т.к. частота вращения малая, то система возбуждения многополюсная.
У синхронного генератора при многополюсной системе возбуждения – роторы выполняется явнополюсными, а при двухполюсной системе возбуждения –неявнополюсными.
Действующее значение эдс фазы якорной обмотки синхронного генераторапри синусоидальной форме эдс, индуцируемой в проводах равноЕ=4,44fwkобФо, гдеw– число витков фазы якорной обмотки;kоб– обмоточный коэффициент.
При ёмкостной и индуктивной нагрузке магнитные линии поля ротора Фо и статора Фа коллинеарны.
Уравнение электрического состояния одной фазы СГ с учетом поля рассеяния якоря Фо имеет видЕ0 +Еа + Еσ = U + Rя I
Где Е0 – эдс холостого хода; Еа – эдс самоиндукции обмотки якоря; Еσ – эдс поля рассеяния
Упрощённое уравнение электрического состояния фазы СГ, U = Еа - jXсин I
Электромагнитный момент СГ зависит от фазового сдвига, тока и от фазового потока М = CМ ФIcosφ
Трансформаторы

1 - однофазный, 2 – дроссель, 3 - трехфазный, звезда/звезда, 4 - трехфазный, звезда/треугольник, 5 – автотрансформатор.
Функциональная связь ЭДС обмотки трансформатора, магнитным потоком, числом витков и частотой - Е1 = 4,44fwФ1

Рис.2 Опыт холостого хода - а; опыт короткого замыкания -б; опыт номинальной нагрузки– в.

Рис.3. Зависимость изменения напряжения на зажимах вторичной обмотки трансформатора от коэффициента нагрузки: при индуктивной нагрузке трансформатора φ > 0 , - 1; при ёмкостной нагрузке трансформатораφ < 0, - 3; внешняя характеристика трансформатора - 2.

Рис.4. Схемы замещения: Т – образная эквивалентная схема реального трансформатора – а; упрощенная Г – образная схема трансформатора –б; при коротком замыкании –в.
Потери мощности трансформатора


а. б.
Рис.2. Потери мощности трансформатора а- в проводах обмотки (меди) – 1, в сердечнике (стали) - 2, зависимость КПД от нагрузки – 3,б -энергетическая диаграмма трансформатора.
Справочный материал по электрическим машинами трансформаторам
Машины постоянного тока
Так, из закона электромагнитной индукции следует, что если проводник перемешать перпендикулярно линиям магнитного поля, то в нем будет наводиться эдс, а ее значение определится формулойе = Blυ,
где В — магнитная индукция, В∙с/м2;l,υ — длина, м, и скорость, м/с, перемещения проводника.
Под действием эдс в проводнике, замкнутом на резистор, возникает ток в направлении, совпадающем с направлением эдс. В результате взаимодействия проводника с током и магнитного поля возникнет электромагнитная сила, которая определяется по формуле Fэм=ВIl, а ее направление — поправилу «левой руки».
Уравнение электрического состояния генератора,Е = U + Rя I или U = Е - Rя I
Уравнение электрического состояния двигателя, Е = U - Rя I или U = Е + Rя I
Действующее значение эдс в витке
![]()
Среднее значение эдс в витке в
предположении, чтоФ=Всрlτ
равно
![]()
Если общее число витков, соединенных
последовательно, одной параллельной
ветви равно N/(2а), то эдс на щетках
![]() ,
,
где сЕ=pN/(60a) — конструктивная постоянная обмотки;N — число проводников;а — число параллельных ветвей.
Электродвижущая сила одной фазы якорной
обмотки
![]()
где Eв — эдс витка;kоб — обмоточный коэффициент, учитывающий тип обмотки и отличие геометрической суммы эдс витков от арифметической;w — число витков фазы.
Внешнии характеристики при различных способах возбуждения генератора Рис.1.
 Рис.1.
Рис.1.
1 Характеристика холостого хода генератора ПТ с независимым возбуждением
2 Внешняя характеристика генератора ПТсо смешанным возбуждением
3 Внешняя характеристика генератора ПТс независимым возбуждением
4 Внешняя характеристика генератора ПТс последовательным возбуждением
5 Внешняя характеристика генератора ПТс параллельным возбуждением
Универсальная характеристика машины параллельного возбуждения Рис.2.

Рис.2
1 - Режим генератора, 2 - Режим двигателя, 3 - Режим электромагнитного тормаза
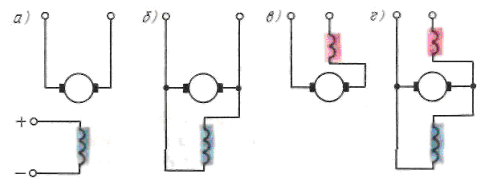
Рис.3. Независимое возбуждение – а;параллельное возбуждение –б; последовательное возбуждение –в; смешанное –г.
Двигатель Постоянного Тока

Рис.4. а -универсальная характеристика машины параллельного возбуждения;
б - механическая характеристика двигателя последовательного возбуждения;
в - механическая характеристика двигателя смешанного возбуждения;
г - механическая характеристика двигателя параллельного возбуждения.
Самовозбуждение генератора происходит при наличи трёх условий
Остаточного магнитного потока, создающего Еост
Совпадающего направления поля обмотки возбуждения с направлением остаточного магнитного потока
Сопротивления обмотки возбуждения (при параллельном возбуждении) меньше критического, т.е. когда ток возбуждения способен достигать значения, обеспечивающего на характеристике холостого хода заданное значение ЕА . (RB >RKP)

Рис.5 Графическое определение режима генератора при самовозбуждении.
Синхронный генератор
Синхронной называется электрическая машина, частота вращение которой связана постоянным отношением с частотой сети переменного тока, в которую машина включена.

Рис.6. Характеристика холостого хода синхронного генератора или магнитная характеристика (влияние тока возбуждения на ЭДС)
Рис.7. Зависимости кпд синхронного генератора от нагрузки при различных коэффициентах мощности
Энергетические потери и диаграммы
Энергетические потери синхронного генератора делятся на постоянные – механические, возбуждения и в стали, а переменные потери – меди и добавочные
КПД синхронного генератора описываются формулой
η= 3UIcosφ/(3UIcosφ +Pпост + Pперем)
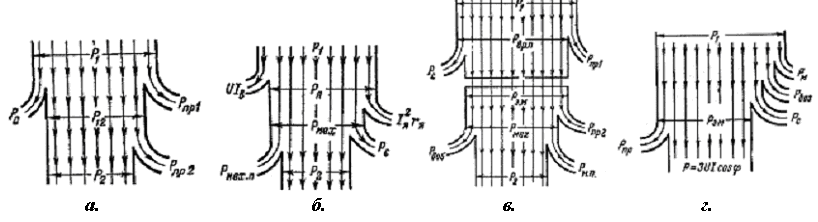
Рис.8 а - энергетическая диаграмма трансформатора;б - энергетическая диаграмма двигателя постоянного тока;в - энергетическая диаграмма асинхронного двигателя;г - энергетическая диаграмма синхронного генератора.
Максимальная частота вращения синхронной машины в сети переменного тока с частотой 50 Гц - 2πf(3000)
Если количество пар полюсов р1>р2, то частота вращения ротора -n1<n2
синхронной машины уменьшится. (n=2πf/p)
У гидрогенераторов первичным двигателем является гидротурбина, т.к. частота вращения малая, то система возбуждения многополюсная.
У синхронного генератора при многополюсной системе возбуждения – роторы выполняется явнополюсными, а при двухполюсной системе возбуждения –неявнополюсными.
Действующее значение эдс фазы якорной обмотки синхронного генераторапри синусоидальной форме эдс, индуцируемой в проводах равноЕ=4,44fwkобФо, гдеw– число витков фазы якорной обмотки;kоб– обмоточный коэффициент.
При ёмкостной и индуктивной нагрузке магнитные линии поля ротора Фо и статора Фа коллинеарны.
Уравнение электрического состояния одной фазы СГ с учетом поля рассеяния якоря Фо имеет видЕ0 +Еа + Еσ = U + Rя I
Где Е0 – эдс холостого хода; Еа – эдс самоиндукции обмотки якоря; Еσ – эдс поля рассеяния
Упрощённое уравнение электрического состояния фазы СГ, U = Еа - jXсин I
Электромагнитный момент СГ зависит от фазового сдвига, тока и от фазового потока М = CМ ФIcosφ
Трансформаторы

1 - однофазный, 2 – дроссель, 3 - трехфазный, звезда/звезда, 4 - трехфазный, звезда/треугольник, 5 – автотрансформатор.
Функциональная связь ЭДС обмотки трансформатора, магнитным потоком, числом витков и частотой - Е1 = 4,44fwФ1

Рис.2 Опыт холостого хода - а; опыт короткого замыкания -б; опыт номинальной нагрузки– в.

Рис.3. Зависимость изменения напряжения на зажимах вторичной обмотки трансформатора от коэффициента нагрузки: при индуктивной нагрузке трансформатора φ > 0 , - 1; при ёмкостной нагрузке трансформатораφ < 0, - 3; внешняя характеристика трансформатора - 2.

Рис.4. Схемы замещения: Т – образная эквивалентная схема реального трансформатора – а; упрощенная Г – образная схема трансформатора –б; при коротком замыкании –в.
Потери мощности трансформатора


а. б.
Рис.2. Потери мощности трансформатора а- в проводах обмотки (меди) – 1, в сердечнике (стали) - 2, зависимость КПД от нагрузки – 3,б -энергетическая диаграмма трансформатора.

 опыта
опыта