
УЧЕБА / Прекционное черчение
.pdf
39
Пример построения линии на сфере
Рис. 37. Построение линии на сфере
Дано: Φ – сфера – поверхность общего вида.
———————
m (m2) – ?
Анализ условия(рис. 37)
Линия m лежит в плоскости α, расположенной под
углом к П1 и П3. m – окружность.
α& Π2 * m2 –
отрезок.
α! Π1 * m1 –
эллипс.
α! Π3 * m3 –
эллипс.
m2 – известна (α – проецирующая
на П2).
————————
m1 и m3 – ?
Порядок решения:
1. Опорные точки: A1B1 и A3B3 – малые оси эллипсов (AB – диаметр окружности); C1D1 и C3D3 – большие оси эллипсов (CD – диаметр окружности);
AB & CD.
Точки видимости на Π1: точки 1 и 2, принадлежат границе видимости сферы на Π1 (экватору).
Точки видимости на Π3: точки 3 и 4, принадлежат границе видимости сферы на Π3 (профильному меридиану).
2.Промежуточные точки строятся, исходя из условия принадлежности параллелям (окружностям) на сфере (см. «Построение точек на поверхности сфе-
ры», стр. 37).
Соединяем полученные точки плавной кривой по лекалам, следя за симметричностью эллипсов относительно большой и малой осей.
3.Видимость. На плоскости Π1 видима часть эллипса, расположенная выше экватора. В точках 11 и 21 видимость меняется, и часть кривой, лежащая ниже экватора, невидима. На Π3 видима часть эллипса, расположенная ближе границы видимости, от точки A3 до точек 33 и 43. К точке B3 уходит невидимая часть эллипса.

40
Пример построения выреза в шаре
Рис. 38. Задание для построения выреза в шаре
Анализ условия (чтение исходного чертежа) (рис. 38)
Дано: 1. Шар, ограниченный сферической поверхностью – поверхностью общего вида.
2.Сквозное призматическое отверстие, образованное тремя плоскостями, занимающими проецирующее положение по отношению к
П2 (собирательное свойство фронтальной проекции отверстия).
Вывод: фронтальные проекции линий пересечения известны, необходимо построить их горизонтальные и профильные проекции.
Порядок решения:
1. Строим изображение сферы (рис. 39) без учета отверстия. Для этого необходимо построить проекции центра сферы и очерки сферы на плоскостях проекций – окружности, диаметр которых равен диаметру сферы.
2. Строим проекции линий пересечения каждой плоскости, ограничивающей отверстие, со сферической поверхностью на плоскостях проекций П1 и П2.
Рассмотрим, как пересекается сфера каждой плоскостью отверстия.
а) Нижняя плоскость отверстия лежит в плоскости α, которая является горизонтальной плоскостью уровня. В результате пересечения сферы с плоскостью α образуется окружность, горизонтальная проекция которой – окружность радиуса R, а профильная проекция – отрезок. Но в вырез попадает не вся окружность, а две дуги между точками 1, 2 и точками 1′, 2′. Находим горизонтальные проекции точек 1, 2, 1′, 2′ на построенной горизонтальной проекции окружности, а затем их профильные проекции.
На П1 окружность будет невидима, так как лежит ниже границы видимости на П1. На П3 будет видна часть окружности до точек видимости на П3 – 6 и 6′, расположенная ближе границы видимости на П3. Точки 1 и 1' видимы на П3, а точки 2 и 2′ невидимы.
б) В результате пересечения сферы с плоскостью β образуется окружность. Плоскость β является профильной плоскостью уровня, поэтому окружность на П3 изобразится в виде окружности, а на П1 – в виде отрезка. Но в вырез попадает не вся окружность, а две дуги между точками 2, 3 и точками 2′, 3′.
На П3 окружность будет невидима, так как лежит за границей видимости на П3. На П1 будет видна часть окружности до точек видимости на П1 – 5

41
и 5′, расположенная выше границы видимости на П1. Точки 3 и 3′ видимы на П1, а точки 2 и 2′ невидимы.
Рис. 39. Построение выреза в шаре
в) При пересечении сферы плоскостью γ на сферической поверхности образуется окружность. AB – диаметр окружности. Плоскость γ расположена под углом к плоскостям проекций П1 и П3, поэтому окружность изобразится на них в виде эллипсов. Эллипсы строятся полностью, а затем выделяются участки, попадающие в вырез, с учетом видимости.
Опорные точки: А1В1 и А3В3 – малые оси эллипсов; С1D1 и С3D3 – большие оси эллипсов; 4 и 4′ – точки видимости на П1; 7 и 7′ – точки видимости на П3.
Промежуточные точки строятся, исходя из условия принадлежности точки сфере (вспомогательные окружности на сфере в плоскостях, парал-
лельных П1).
Соединяем полученные горизонтальные и профильные проекции точек плавными кривыми с учетом видимости, следя за симметричностью относительно большой и малой осей эллипсов.
42
3.Строим проекции линий пересечения плоскостей призматического отверстия: 11′ – проекция линии пересечения плоскостей α и γ, 22′ – проекция линии пересечения плоскостей α и β, 33′ – проекция линии пересечения плоскостей β и γ.
4.Удаляем части поверхности сферы, вырезанные отверстием. Это участки горизонтального очерка сферы между точками 4, 5 и 4′, 5′, участки профильного очерка сферы между точками 6, 7 и 6′, 7′, а также части сферической поверхности,
ограниченные плоскостями выреза. На П1 части окружности в плоскости α оказываются незакрытыми и становятся видимыми до эллипса; на П3 видимы части окружности в плоскости β, не закрытые плоскостью γ до эллипса.
5.Обводим проекции сферы и полученные линии выреза.
3. Аксонометрические проекции
Метод прямоугольного проецирования на несколько плоскостей проекций, обладая многими достоинствами, вместе с тем имеет существенный недостаток: изображения не обладают наглядностью.
Чтобы исправить этот недостаток, применяют способ аксонометрического проецирования. Он заключается в том, что данный предмет вместе с системой трех взаимно перпендикулярных осей координат, к которой он отнесен в пространстве, проецируется на картинную плоскость. Проекция на этой плоскости называется аксонометрической, или аксонометрией.
Основная формула аксонометрии mx2 , n2y , pz2 - 2 , ctg2+ ,
где mx – коэффициент искажения по оси x; ny – коэффициент искажения по оси y; pz – коэффициент искажения по оси z; φ – угол проецирования.
3.1. Виды аксонометрических проекций
В зависимости от соотношения коэффициентов искажения различают следующие виды аксонометрических проекций:
!" изометрия (mx = ny = pz);
!" диметрия (mx = pz ≠ ny); !" триметрия (mx ≠ ny ≠ pz).
Если φ = 90˚, то аксонометрическая проекция называется прямоугольной.
Если φ ≠ 90˚, то косоугольной.
Из всех видов аксонометрических проекций рекомендуется применять те, которые меньше искажают натуральный вид предмета и наиболее удобны для построения.
На практике наибольшее распространение получили прямоугольные изометрическая и диметрическая проекции, установленные ГОСТ 2.317–69 (табл. 1).

43
|
|
|
|
|
Таблица 1 |
|
|
|
|||
Прямоугольная изометрия |
|
Прямоугольная диметрия |
|||
|
|
|
|||
mx = ny = pz |
mx = pz, ny = 0,5mx |
|
|||
φ = 90º, ctg φ = 0 |
φ = 90º, ctg φ = 0 |
|
|||
3m2 - 2 % mx = 0,82 |
2m2 |
, .0,5m |
x |
/2 - |
2 % m = 0,94 |
x |
x |
|
|
x |
|
mx = ny = pz = 0,82 – натуральные ко- |
mx = pz = 0,94; ny = 0,47 – натуральные ко- |
||||
эффициенты искажения по осям |
эффициенты искажения по осям (мас- |
||||
(масштаб 1:1). |
штаб 1:1). |
|
|
|
|
На практике: |
На практике: |
|
|
||
mx = ny = pz = 1 – приведенные коэф- |
mx = pz = 1; ny = 0,5 – приведенные коэф- |
||||
фициенты искажения по осям (аксо- |
фициенты искажения по осям (аксоно- |
||||
нометрический масштаб 1,22:1) |
метрический масштаб 1,06:1) |
||||
|
|
||||
Все отрезки, расположенные по осям |
Отрезки, расположенные по осям x и z |
||||
или параллельно осям, откладыва- |
или параллельно им откладываются в на- |
||||
ются в натуральную величину |
туральную величину, а отрезки по оси у |
||||
|
или ей параллельные, делятся пополам |
||||
|
|
|
|
|
|
3.2. Аксонометрические проекции плоских фигур
3.2.1. Построение плоских многоугольников
Построение изображений плоских многоугольников сводится к построению аксонометрических проекций их вершин, которые затем соединяют прямыми линиями.
Пример построения в аксонометрии плоского пятиугольника, расположенного в горизонтальной плоскости, приведен на рис. 40.

44
à
á |
â |
Рис. 40. Комплексный чертеж (а), прямоугольные изометрия (б) и диметрия (в) плоского пятиугольника
3.2.2. Построение окружности
Аксонометрической проекцией окружности является эллипс. Эллипс – лекальная кривая, которую строят по точкам, что достаточно трудоемко. Поэтому при изображении окружностей, расположенных в координатных плоскостях, эллипсы заменяют четырехцентровыми овалами (циркульными кривыми).
Расположение осей эллипсов и примеры построения овалов показаны в табл. 2.

|
45 |
Таблица 2 |
|
|
|
|
|
|
Прямоугольная изометрия |
Прямоугольная диметрия |
|
|
|
|
|
|
|
АВ – большая ось эллипса |
АВ – большая ось эллипса |
|
СD – малая ось эллипса |
СD – малая ось эллипса |
|
Малая ось & большой оси |
Малая ось & большой оси |
|
хоу: большая ось & z |
хоу: большая ось & z |
xoz: большая ось & y |
xoz: большая ось & y |
AB = 1,06d |
AB = 1,06d |
yoz: большая ось & x |
CD = 0,35d |
CD = 0,95d |
AB = 1,22d |
yoz: большая ось & x |
|
CD = 0,71d |
AB = 1,06d |
|
|
CD = 0,35d |
|
Построение овала |
Построение овала |
Построение овала |
|
|
|
3.3. Аксонометрические проекции геометрических тел
Построение изображений геометрических тел в аксонометрии заключается в построении аксонометрических проекций геометрических элементов, их составляющих. Например, построение аксонометрии шестигранной призмы заключается в построении нижнего основания – плоского шестиугольника, а затем параллельных оси z ребер, вершины которых соединяют прямыми (рис. 41).

46
à |
á |
â |
Рис. 41. Комплексный чертеж (а), прямоугольные изометрия (б) и диметрия (в) шестигранной призмы
Прямоугольной изометрией шара является окружность с диаметром, равным 1,22 диаметра шара (при построении с применением приведенных коэффициентов искажения). На рис. 42 приведена изометрическая проекция шара с вырезом одной восьмой части тремя координатными плоскостями, проходящими через центр шара.
При рассечении поверхности шара плоскостями получаются окружности, которые изображаются в виде эллипсов, для простоты заменяемыми овалами. Точки пересечения овалов между собой определяют границы выреза.
Прямоугольной диметрией шара является окружность с диаметром, равным 1,06 диаметра шара (при построении по приведенным коэффициентам искажения).
На рис. 43 приведены комплексный чертеж и изометрия предмета, выполнение которой сводится к построению изометрических проекций геометрических тел, составляющих предмет: призмы, цилиндра, конуса.
Рис. 42. Шар с вырезом 1/8 части |
Рис. 43. Комплексный чертеж и изометрия |
в изометрии |
совокупности геометрических тел |

47
4.Изображения
Всоответствии с ГОСТ 2.305–68 изображения предметов должны выполняться по методу прямоугольного (ортогонального) проецирования. Следует обратить внимание на различие, существующее между изображением и проекцией предмета.
Проекция – однозначное точечное соответствие, которое состоит в том, что каждой точке предмета соответствует определенная точка на проекции и наоборот.
Изображение отличается от проекции тем, что при построении изображений стандарт допускает применение условностей и упрощений.
При проецировании предмет располагают между наблюдателем и соответствующей плоскостью проекций. Изображение на фронтальной плоскости проекций принимается на чертеже в качестве главного. При этом предмет располагают так, чтобы главное изображение несло наиболее полную информацию о форме и размерах предмета.
Изображения на чертежах в зависимости от их содержания разделяются на
виды, разрезы, сечения и выносные элементы:
Изображения
Виды |
Разрезы |
Сечения |
Выносные элементы |
|
|
|
|
4.1. Виды
Вид – изображение обращенной к наблюдателю видимой части поверхности предмета. Виды разделяются на основные, дополнительные и местные:
Виды
основные |
местные |
дополнительные |
|
|
|
Образуются на основных плоскостях про- |
Образуются на плоскостях, не параллель- |
|
екций и плоскостях, им параллельных |
ных основным плоскостям проекций |
|
4.1.1. Основные виды
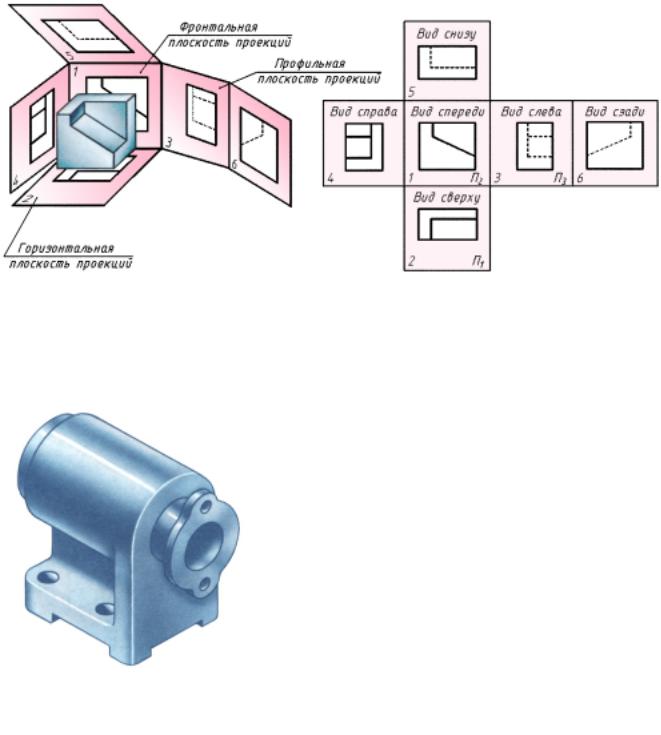
Основные виды – это изображения, получаемые на основных плоскостях проекций и плоскостях, им параллельных. Для этого предмет мысленно помещают внутри пустотелого куба и проецируют его на внутренние поверхности граней. Затем грани совмещают с плоскостью, как показано на рис. 44. Названия основных видов соответствуют направлению взгляда на плоскость:
1 – вид спереди (главный вид);
2 – вид сверху;
3– вид слева;
4– вид справа;
5– вид снизу;
6– вид сзади.
Пример изображения детали на основных видах приведен на рис. 45.
48
à |
á |
Рис. 44. Образование (а) и расположение (б) основных видов на чертеже
à |
á |
Рис. 45. Деталь (а) и ее изображение на основных видах (б)
4.1.2. Дополнительные виды
Дополнительный вид – изображение, полученное на плоскостях, не параллельных основным плоскостям проекций. Дополнительные виды применяются в тех случаях, если какую-либо часть предмета невозможно показать на основных видах без искажения формы и размеров (рис. 46).
