
УЧЕБА / Мутодичка
.pdf
21
Таблица №7 Данные к задачам №5 и №6
№ |
Условие задачи |
п/п |
|
1Определить расстояние от точки А до плоскости α(В; С; D).
2Построить прямоугольный равнобедренный треугольник AMN с гипотенузой MN на прямой BC.
3Построить точку А, симметричную точке В относительно отрезка CD.
4Через точку А провести прямую, пересекающую отрезок ВС под углом 45º.
5Построить недостающие проекции сторон прямоугольника ABCD.
6Построить квадрат AMNK с диагональю MK на прямой BD.
7Определить недостающую проекцию точки А, равноудаленной от концов отрезка ВС.
8Построить прямоугольный равнобедренный треугольник AMN с катетом MN на прямой BC.
9На отрезке AD найти точку K, равноудаленную от концов отрезка BC.
10Построить квадрат AMNK со стороной MN на прямой BC.
11Построить точку К, симметричную точке D относительно плоскости α(A; В; С).
12Построить равнобедренный треугольник AMN с основанием MN, равным 60 мм, на отрезке BC.
13Определить величину двугранного угла, образованного треугольниками ABC и BCD.
14На прямой АВ найти точки M и N, удаленные от точки С на 55 мм.
15Построить высоту AD в треугольнике АВС.
16Построить недостающую проекцию отрезка АВ, если отрезок АВ перпендикулярен отрезку ВС.
17Найти центр окружности, вписанной в треугольник АВС.
18Построить равносторонний треугольник AMN со стороной MN на отрезке BC.
19Построить проекции сферы с центром в точке D, касающейся плоскости α(A; В; С).
20Найти центр окружности, описанной около треугольника АВС.
22
7.1.4 Лист 4
Задача №7. Построить недостающую проекцию линии, принадлежащей поверхно-
сти. Данные для решения задачи приведены в таблицах 8 и 9.
Указания к решению задачи №7.
В правой половине листа намечают оси координат, начало координат на расстоянии 5…10 мм от рамки чертежа. В зависимости от варианта данная проекция линии является ломаной, либо дугой окружности. В последнем случае дуга окружности задается проекциями трех точек, и для ее изображения необходимо найти центр этой окружности.
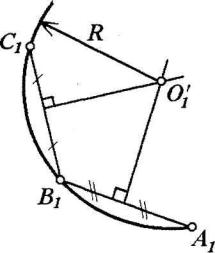
Пусть дуга является горизонтальной (или фронтальной) проекцией линии и задана проекциями точек А, В и С (рисунок 8). Соединим проекции этих точек отрезками прямых линий АВ и ВС. Каждый из этих отрезков делится пополам, и через их середины проводим перпендикуляры к ним. Точка пересечения перпендикуляров О' принимается за центр дуги окружности.
Рисунок 8
Пример выполнения листа 4 - Приложение 4.
23
Таблица №8 Данные к задаче №7
|
|
Поверхность |
|
|
Координаты точек |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ва- |
Но- |
Координа- |
|
|
|
|
|
|
|
|
|
|
||
ри- |
ты точки |
|
|
А |
|
|
В |
|
|
С |
|
|||
мер |
Форма |
|
|
|
|
|
|
|||||||
ант |
|
О |
|
|
|
|
|
|
|
|
|
|
||
фи- |
|
|
линии |
|
|
|
|
|
|
|
|
|
||
|
x |
y |
z |
X |
y |
z |
x |
y |
z |
x |
y |
z |
||
|
гуры |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
70 |
50 |
0 |
дуга |
85 |
- |
40 |
45 |
- |
60 |
60 |
- |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
70 |
50 |
0 |
ломаная |
50 |
50 |
- |
90 |
50 |
- |
70 |
35 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
70 |
55 |
0 |
ломаная |
70 |
- |
60 |
50 |
- |
20 |
100 |
- |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
70 |
60 |
0 |
ломаная |
80 |
- |
60 |
45 |
- |
25 |
100 |
- |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
70 |
60 |
0 |
дуга |
55 |
35 |
- |
55 |
75 |
- |
100 |
75 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
6 |
80 |
50 |
0 |
ломаная |
50 |
30 |
- |
80 |
80 |
- |
100 |
30 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
7 |
70 |
60 |
0 |
ломаная |
100 |
40 |
- |
45 |
40 |
- |
85 |
90 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
8 |
70 |
50 |
0 |
дуга |
90 |
50 |
- |
50 |
50 |
- |
70 |
70 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
9 |
100 |
60 |
0 |
ломаная |
90 |
- |
70 |
60 |
- |
40 |
115 |
- |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
70 |
50 |
0 |
ломаная |
100 |
- |
10 |
40 |
- |
30 |
70 |
- |
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
2 |
70 |
50 |
0 |
дуга |
50 |
50 |
- |
90 |
50 |
- |
70 |
30 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
3 |
70 |
55 |
0 |
дуга |
100 |
70 |
- |
60 |
70 |
- |
60 |
20 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
4 |
70 |
60 |
0 |
дуга |
110 |
50 |
- |
75 |
70 |
- |
55 |
35 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
5 |
70 |
60 |
0 |
ломаная |
95 |
75 |
- |
45 |
75 |
- |
45 |
35 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
6 |
80 |
50 |
0 |
ломаная |
90 |
- |
20 |
35 |
- |
0 |
60 |
- |
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
7 |
70 |
60 |
0 |
ломаная |
50 |
- |
20 |
85 |
- |
60 |
115 |
- |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
8 |
70 |
50 |
0 |
дуга |
90 |
40 |
- |
50 |
40 |
- |
70 |
65 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
9 |
100 |
60 |
0 |
ломаная |
80 |
95 |
- |
130 |
60 |
- |
80 |
35 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
1 |
70 |
50 |
0 |
дуга |
90 |
40 |
- |
75 |
70 |
- |
45 |
50 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
2 |
70 |
50 |
0 |
дуга |
90 |
- |
30 |
70 |
- |
0 |
50 |
- |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
3 |
70 |
55 |
0 |
ломаная |
90 |
75 |
- |
40 |
75 |
- |
80 |
15 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
4 |
70 |
60 |
0 |
ломаная |
100 |
80 |
- |
35 |
80 |
- |
80 |
30 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
5 |
70 |
60 |
0 |
дуга |
100 |
60 |
- |
75 |
75 |
- |
55 |
35 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
6 |
80 |
50 |
0 |
дуга |
70 |
80 |
- |
110 |
50 |
- |
70 |
30 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
7 |
70 |
60 |
0 |
дуга |
100 |
80 |
- |
60 |
80 |
- |
60 |
30 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
8 |
70 |
50 |
0 |
ломаная |
85 |
- |
55 |
50 |
- |
40 |
100 |
- |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
9 |
100 |
60 |
0 |
ломаная |
100 |
- |
20 |
50 |
- |
40 |
90 |
- |
65 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24
Таблица №9 Данные к задаче №7
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
25
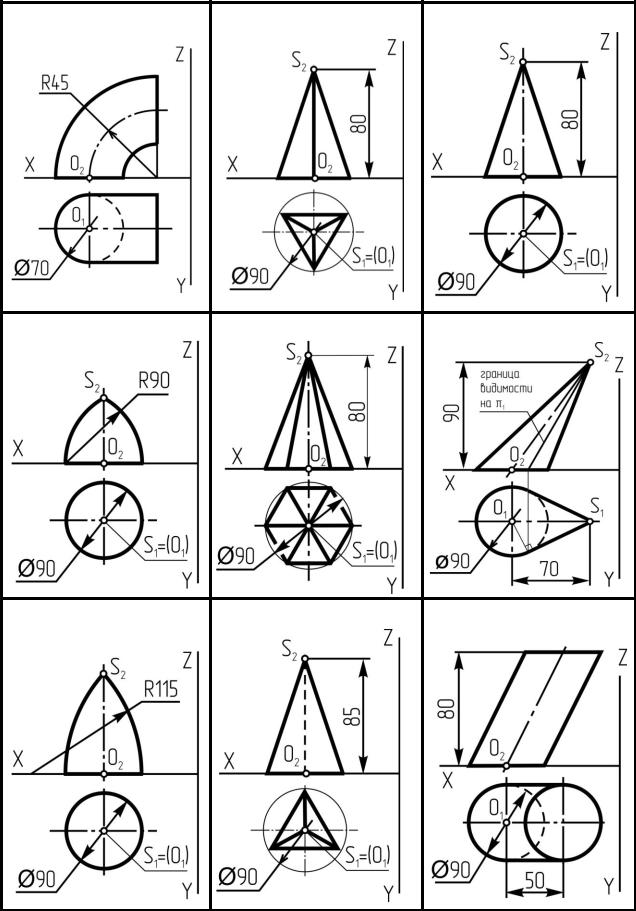
Задача №8. Построить проекции пирамиды, основанием которой является треугольник ABC, а ребро AS определяет высоту h пирамиды. Дан-
ные к решению задачи взять из таблицы 10.
Указания к решению задачи №8.
Влевой половине листа намечают оси координат и в соответствии с вариантом задания строятся проекции основания пирамиды - точки А (А1; А2), В (В1; В2), С (С1; С2).
Впостроенном треугольнике ABC (A1B1C1, A2B2C2) в точке А восстанавливается перпендикуляр n (n1; n2), для чего предварительно проводят главные линии плоскости: горизонталь h (h1; h2) и фронталь f (f1; f2).
На этом перпендикуляре выбирают произвольную точку К (К1; К2).
Методом вращения вокруг проецирующей оси (на чертеже ось обозначить) определяют натуральную величину отрезка АК и на этом направлении откладывают заданную высоту пирамиды. Затем обратным преобразованием определяется положение вершины пи-
рамиды S (S1, S2). Строятся ребра пирамиды AS, BS, CS. С помощью конкурирующих точек (3-4, 5-6) расположенных на скрещивающихся прямых (стороне основания и ребре пирамиды) определяют их видимость. Видимые ребра и стороны основания обвести сплошной толстой линией невидимые - штриховыми. Все вспомогательные тонкие линии построения на чертеже сохранить. Пример выполнения в приложении 4.
7.1.5 Лист 5
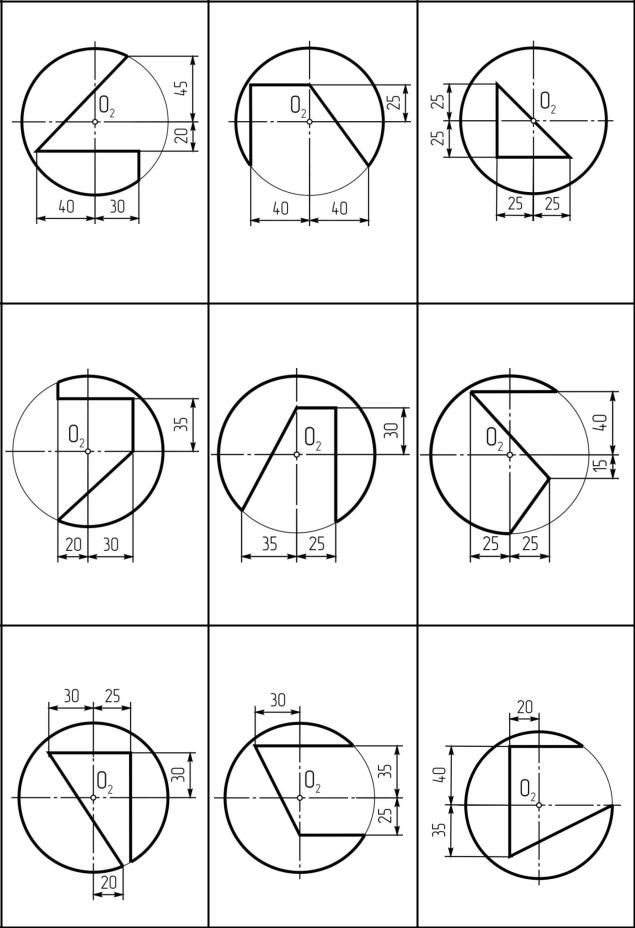
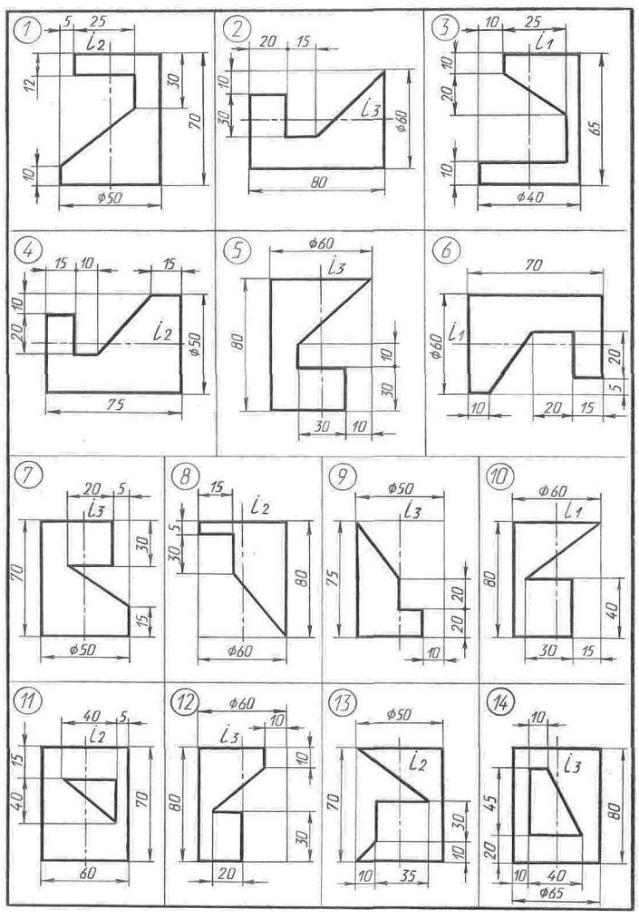
Задача № 9. Построить сферу с вырезом в трех проекциях. Данные для решения задачи взять из таблицы 11. Размеры на чертеже не проставлять.
Указания к решению задачи №9.
На листе формата A3 от левой линии рамки отложить 110 мм, от верхней -150мм, и отметить точку О123 (начало координат). От этой точки построить точку О´ (О1´, О´2, О´3) - центр сферы с координатами О´(55, 55, 55). Затем построить три проекции сферы радиуса 50 мм. Пример выполнения в приложении 5.
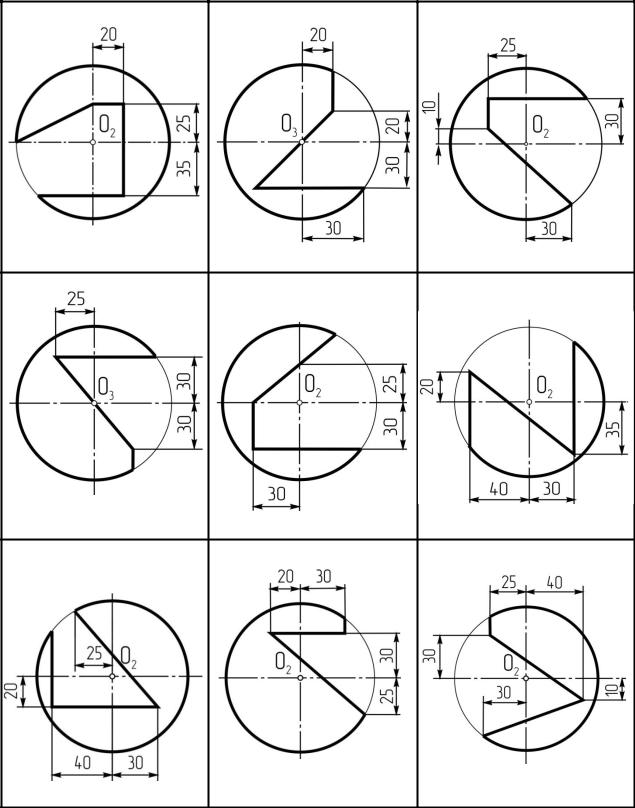
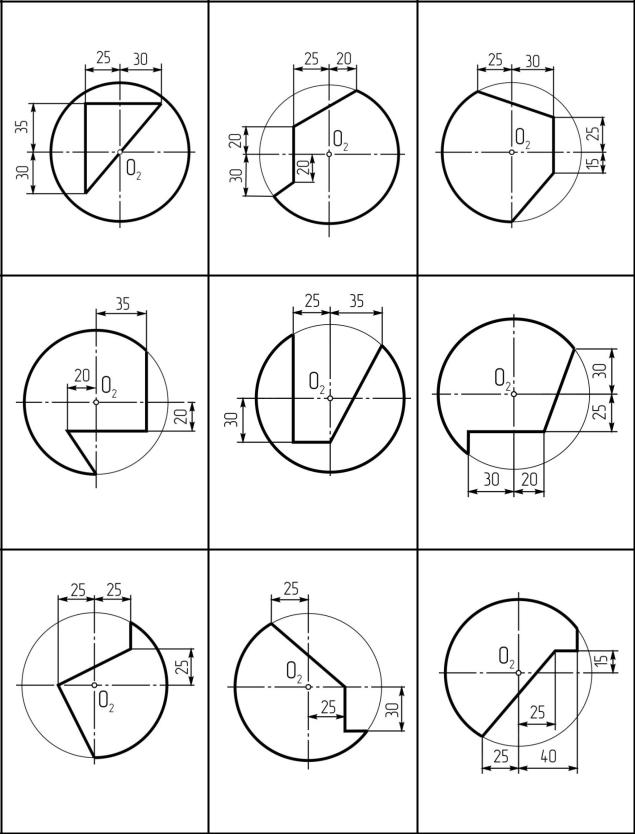
Задача №10. Построить три проекции цилиндра с вырезом. Данные для решения за-
дачи взять из таблицы 12. Размеры на чертеже не проставлять.
Указания к решению задачи №10.
На оставшейся части листа разместить три проекции цилиндра. По указанным размерам построить линии сквозного выреза, обратив внимание на заданную ось цилиндра. Построение недостающих проекций линий начинают с определения характерных точек и их обозначают буквами.
Вспомогательные тонкие линии сохраняют на чертеже. Обводят с учетом видимости очерки цилиндра и линии выреза в трех плоскостях проекций. Пример выполнения в приложении 5.
26
Таблица №10. Данные к задаче №8.
Вари- |
|
А |
|
|
В |
|
|
|
С |
|
Н |
|
|
|
|
|
|
|
|
|
|
||
ант |
x |
у |
z |
x |
у |
z |
|
x |
у |
z |
|
|
|
||||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
115 |
90 |
10 |
50 |
25 |
80 |
0 |
|
85 |
45 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
120 |
90 |
10 |
50 |
20 |
70 |
|
0 |
80 |
50 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
115 |
90 |
10 |
50 |
25 |
80 |
|
0 |
80 |
45 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
120 |
95 |
10 |
55 |
20 |
75 |
|
0 |
80 |
45 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
115 |
10 |
90 |
50 |
80 |
25 |
|
0 |
50 |
80 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
115 |
10 |
85 |
45 |
80 |
25 |
|
0 |
50 |
60 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
120 |
10 |
90 |
50 |
80 |
20 |
|
0 |
50 |
70 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
115 |
10 |
85 |
50 |
80 |
25 |
|
0 |
45 |
80 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
115 |
10 |
90 |
50 |
80 |
25 |
|
0 |
50 |
70 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
20 |
10 |
90 |
80 |
80 |
25 |
|
125 |
50 |
80 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
20 |
15 |
90 |
85 |
80 |
25 |
|
125 |
40 |
85 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
15 |
10 |
85 |
80 |
80 |
20 |
|
130 |
50 |
80 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
13 |
15 |
10 |
90 |
85 |
80 |
25 |
|
130 |
50 |
80 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
14 |
20 |
10 |
85 |
85 |
80 |
25 |
|
135 |
50 |
70 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
15 |
20 |
90 |
10 |
85 |
25 |
80 |
|
135 |
80 |
50 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
16 |
20 |
40 |
75 |
85 |
120 |
5 |
|
130 |
50 |
40 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
17 |
20 |
75 |
40 |
85 |
5 |
110 |
|
130 |
40 |
50 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
18 |
120 |
75 |
40 |
50 |
5 |
110 |
|
0 |
40 |
50 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
19 |
120 |
40 |
75 |
50 |
120 |
5 |
|
0 |
5 |
40 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
20 |
120 |
40 |
75 |
50 |
110 |
5 |
|
0 |
45 |
40 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
21 |
125 |
40 |
75 |
50 |
110 |
10 |
|
0 |
50 |
40 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
22 |
20 |
40 |
10 |
85 |
110 |
80 |
|
135 |
50 |
50 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
23 |
20 |
10 |
40 |
85 |
80 |
110 |
|
135 |
50 |
40 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
24 |
120 |
40 |
10 |
50 |
110 |
80 |
|
0 |
50 |
50 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
25 |
120 |
10 |
40 |
50 |
80 |
110 |
|
0 |
50 |
45 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
26 |
20 |
40 |
10 |
85 |
110 |
80 |
|
125 |
50 |
40 |
85 |
|
|
|
|
|
|
|
|
|
|
|
|
27 |
20 |
10 |
40 |
85 |
80 |
110 |
|
130 |
50 |
45 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
27
Таблица №11. Данные к задаче №9.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
28
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
29
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
30
Таблица №12. Данные к задаче №10.
