УЧЕБА / Мутодичка

2

УДК 514.18(075.5)

Л. В. Куркина, Н. В. Ломских, Н. С. Николаенко Начертательная геометрия: Методические указания и задания к домашним кон-

трольным работам для студентов всех специальностей заочной формы обучения. – Барнаул: Издательство АлтГТУ, 2014. – 53 с.

В данном пособии содержатся сведения об оформлении контрольных работ, методические указания к решению всех задач с примерами их решения на чертежах, а также рабочая программа по начертательной геометрии.

Рассмотрено и одобрено на заседании кафедры «Начертательная геометрия и инженерная графика»

Протокол №1 от 29.08. 14 г.

3

Содержание

4

Введение

Начертательная геометрия является одной из общетехнических дисциплин, составляющих основу инженерного образования. В курсе начертательной геометрии изучаются способы построения изображений пространственных фигур на плоскости. Изображения, построенные по определенным законам, дают информацию о форме изображенных предметов и их взаимном расположении в пространстве, позволяют определить их размеры, исследовать другие геометрические свойства.

Изучение начертательной геометрии необходимо для приобретения знаний и умений, позволяющих составлять и читать технические чертежи. Начертательная геометрия является наилучшим средством развития у человека пространственного воображения.

При изучении курса студентами заочной формы обучения необходимо, прежде всего, ознакомиться с рабочей программой, приобрести необходимую учебную литературу.

Самостоятельная работа студента складывается из:

1)изучения теоретической части курса по учебнику;

2)решения задач по каждому разделу курса;

3)выполнения домашней контрольной работы.

Втечение всего учебного года для студентов-заочников на кафедре начертательной геометрии и графики проводятся очные консультации.

Во время экзаменационной сессии организуются лекционные и практические занятия. Итогом изучения курса является зачет или экзамен.

1Учебная программа по начертательной геометрии

1)Предмет начертательной геометрии. Метод проецирования.

2)Комплексный чертеж точки. Взаимное расположение точек.

3)Комплексный чертеж прямой. Прямые общего и частного положения. Взаимное расположение прямых. Теорема о проецировании прямого угла. Нахождение натуральной величины отрезка способом прямоугольного треугольника.

4)Комплексный чертеж плоскости. Плоскости общего и частного положения. Условие принадлежности точки и прямой плоскости. Главные линии плоскости.

5)Параллельность и перпендикулярность прямых и плоскостей. Пересечение прямой с плоскостью.

6)Методы преобразования комплексного чертежа. Метод замены плоскостей проекций и метод вращения вокруг проецирующей оси.

7)Метрические задачи. Определение натуральных величин плоских фигур. Определение расстояний между геометрическими образами (определение расстояния от точки до прямой, от точки до плоскости, между параллельными прямыми). Определение углов между геометрическими образами (между пересекающимися прямыми, между скрещивающимися прямыми, между плоскостями).

8)Комплексный чертеж кривых линий. Плоские и пространственные кривые. Проекции окружности.

5

9)Комплексный чертеж поверхности. Способы задания поверхностей. Контур

иочерк поверхности. Классификация поверхностей.

10)Поверхности вращения (конус, цилиндр, сфера). Точка и линия на поверхности вращения.

11)Пересечение поверхности с плоскостью. Пересечение поверхности с плос-

костью частного положения. Сечения сферы, цилиндра, конуса. 12)Взаимное пересечение поверхностей. Принцип определения точек, о б-

щих для двух поверхностей. Опорные точки линии пересечения. Способы секущих плоскостей и секущих сфер. Пересечение поверхностей в случае, если одна из них занимает проецирующее положение.

13)Пересечение прямой с поверхностью.

14)Развертка многогранных и кривых поверхностей. Общие принципы построения разверток поверхностей. Развертывание цилиндрических и конических поверхностей общего вида. Приближенное развертывание неразвертывающихся поверхностей.

2 Работа с учебной литературой

Основная форма работы студента-заочника - самостоятельное изучение указанного материала по учебнику. Учебную литературу по начертательной геометрии следует не просто «читать», необходимо параллельно с чтением текста воспроизводить все описываемые построения. Чертежи нужно выполнять аккуратно, с помощью чертежных инструментов, с нанесением всех обозначений. Свои знания можно проверять с помощью контрольных вопросов, помещенных в учебнике.

При изучении теоретического материала по учебнику рекомендуется вести конспект. В конспекте следует записывать основные положения теории, теоремы курса и порядок решения типовых задач.

3 Литература

1. Локтев О. В. Краткий курс начертательной геометрии : [ учеб. для втузов] / О. В. Локтев. - Изд. 6-е, стер. - М.: Высш. шк., 2006. - 136 с.: ил. (45 экз.)

2. Чекмарев А. А. Начертательная геометрия и черчение : учеб. для вузов по техн. специальностям / А. А. Чекмарев. - Изд. 2-е, перераб. и доп. - М. : ВЛАДОС, 2005. -

472 с. : ил. (115 экз.)

3. Кашкаров Г. М. Курс начертательной геометрии: учебное пособие /Алт. гос. техн. ун-т им. И. И. Ползунова. – Барнаул: Изд-во АлтГТУ, 2005. – 364 с.: ил. ISBN 5-7568- 0505-2 (490 экз.)

6

4 Рабочий план изучения начертательной геометрии

7

5 Контрольная работа

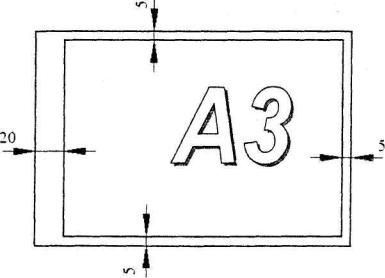
В первом семестре студенты выполняют домашнюю контрольную работу по начертательной геометрии. Контрольная работа содержит 12 задач, которые выполняются на листах ватмана формата A3 (297 420 мм). На каждом листе следует располагать по две задачи. Таким образом, вся контрольная работа выполняется на шести листах указанного формата.

Контрольная работа выполняется по вариантам. Студент выбирает вариант задания пользуясь таблицей (Приложение 1).

Прежде, чем приступить к решению задач на ватмане, необходимо ознакомиться с общими правилами выполнения чертежей, изложенными в стандартах Единой системы конструкторской документации (ЕСКД).

ГОСТ 2.301-68 Форматы ГОСТ 2.302-68 Масштабы ГОСТ 2.303-68 Линии

ГОСТ 2.304-81 Шрифты чертежные На каждом листе выполняется так называемая внутренняя рамка. Она проводится

сплошной толстой линией, как показано на рисунке 1.

Рисунок 1 В правом нижнем углу выполняется основная надпись, в которой студент указывает

свою фамилию, номер группы и вариант.

Все надписи на чертеже должны быть выполнены стандартным шрифтом (предпочтительнее размером №5) в соответствии с ГОСТ 2.304-81.

Характер и толщину линий выбирают в соответствии с ГОСТ 2.303-68. Все линии видимого контура выполняют сплошной основной линией, толщина которой s должна быть в пределах от 0,5 до 1,4 мм (рекомендуемая толщина - 1 мм). Линии невидимого контура изображают штриховой линией. Линии построений и линии связи показывают сплошной тонкой линией (толщина от s/3 до s/2).

Точки на чертеже изображают в виде окружностей диаметром 1,5...2,0 мм и обозначают заглавными буквами латинского алфавита (А, В, С...).

Все вспомогательные построения на чертеже должны быть сохранены. При обводке

8

желательно пользоваться цветными карандашами.

После выполнения контрольной работы все листы следует сброшюровать в альбом. Первый лист (титульный) должен быть оформлен по образцу, приведенному в данном пособии (Приложение 2).

6 Экзамен (зачет)

По окончании изучения курса начертательной геометрии студенты сдают зачет или экзамен (в зависимости от того, какая форма отчетности предусмотрена учебным планом для каждой конкретной специальности).

К зачету (экзамену) допускаются студенты, выполнившие весь объем работ (домашних и аудиторных), определяемый учебной программой.

Зачет принимается при наличии у студента проверенной преподавателем домашней контрольной работы.

Также студентом должны быть сданы на положительные оценки аудиторные контрольные работы, которые выполняются на практических занятиях во время экзаменационной сессии. Объем и содержание таких работ определяет кафедра.

Рекомендуется представить на зачете конспект, который вел студент при изучении курса.

На зачете студент дает объяснение по выполненным им заданиям, а также и по исправлениям к ним, сделанным студентом согласно указаниям преподавателя.

Зачет фиксируется в зачетной книжке и в зачетной ведомости, а работы по начертательной геометрии остаются на хранении на кафедре.

На экзамен студент должен принести:

1)зачетную книжку;

2)конспект учебного материала;

3)альбом домашних контрольных работ, подписанный преподавателем;

4)лист чертежной бумаги формата A3 для решения экзаменационных задач;

5)чертежные инструменты;

6)разрешение на сдачу экзамена (если последний сдается после срока). Проводится экзамен письменно, по билетной системе. Студенту предлагается ре-

шить две задачи и ответить на один теоретический вопрос экзаменационного билета.

7Контрольная работа

7.1Условия задач и указания к их решению

7.1.1Лист 1

Задача №1. Определить натуральную величину отрезка прямой общего положения и углы его наклона к горизонтальной и фронтальной плоскостям проекций.

Указания к решению задачи №1.

Построить горизонтальную и фронтальную проекции отрезка АВ по заданным координатам его концов (данные взять из таблицы 1).

По рисунку 2 видно, что натуральная величина отрезка АВ является гипотенузой прямоугольного треугольника АВ'В. В этом треугольники один катет [АВ'] равен по длине горизонтальной проекции отрезка АВ, т.е. │АВ'│ = │A1B1│, а другой катет [ВВ'] равен разности высот точек А и В, т.е. │ВВ'│ = ZB - ZA = Z.

10

Таблица 1 Данные к задаче №1

Задача №2. Построить недостающую проекцию точки К, принадлежащей плоскости α ( АВС). В плоскости α провести горизонталь на расстоянии Zh от плоскости π1 и фронталь на расстоянии Yf от плоскости π2.

Указания к решению задачи №2.

По заданным координатам точек А, В, С и К (таблица 2) построить горизонтальную и фронтальную проекции плоскости α, заданной треугольником ABC и одну из проекций точки К.

Недостающую проекцию точки К строят исходя из условия принадлежности точки плос-

кости: точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости. Таким образом, через имеющуюся проекцию точки К следует провести вспомогательную прямую, принадлежащую данной плоскости. Вспомогательную прямую удобно провести через точку К и одну из вершин АВС так, чтобы эта прямая пересекала какуюлибо из сторон треугольника. Затем строят вторую проекцию вспомогательной прямой и на ней по линии связи находят недостающую проекцию точки К.

Для построения в плоскости α горизонтали следует вспомнить, что горизонталь плоскости - это прямая, лежащая в плоскости и параллельная плоскости проекций π1.

На чертеже фронтальная проекция горизонтали параллельна оси Х12 (h2 ‖ ОХ).

Фронталь плоскости - это прямая, принадлежащая плоскости и параллельная плоскости проекций π2. Горизонтальная проекция фронтали параллельна оси Х12

(f1 ‖ OX).

После построения горизонталь и фронталь обвести цветными карандашами.